Angular Acceleration

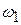If the angular velocity of a rotating body is not constant, then the body has an angular acceleration. Let and be its angular velocities at times 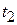and , respectively, The average angular accelerationof the rotating body in the interval from to 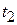is defined as

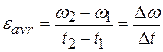11 -7

in which 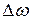is the change in the angular velocity that occurs during the time interval . The (instantaneous) angular acceleration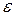, with which we shall be most concerned, is the limit of this quantity as approaches zero. Thus,

11-8

Equations 11-7 and 11-8 hold not only for the rotating rigid body as a whole but also for every particle of that body. The unit of angular acceleration is commonly the radian per second-squared (rad/s²) or the revolution per second-squared (rev/s²).

11-3 Are Angular Quantities Vectors?

We can describe the position, velocity, and acceleration of a single particle by means of vectors. If the particle is confined to a straight line, however, we do not really need vector notation. Such a particle has only two directions available to it, and we can indicate these directions with plus and minus signs.

In the same way, a rigid body rotating about a fixed axis can rotate only clockwise or counterclockwise as seen along the axis, and again we can select between the two directions by means of plus and minus signs. The question arises: "Can we treat the angular displacement, velocity, and acceleration of a rotating body as vectors?" The answer is a qualified "yes"

In the same way, a rigid body rotating about a fixed axis can rotate only clock-

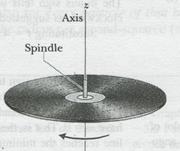Figure 1-l6a
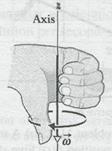Fig. 11-6c

wise or counterclockwise as seen along the axis, and again we can select between the two directions by means of plus and minus signs. The question arises: "Can we treat the angular displacement, velocity, and acceleration of a rotating body as vectors?" The answer is a qualified "yes"

Consider the angular velocity. Figure 1 l-6ashows a vinyl record rotating on a turntable. The record has a constant angular speed 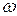= 33 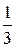rev/min) in the clock-wise direction. We can represent its angular velocity as a vector 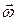pointing along the axis of rotation,. Here's how: We choose the length of this vector according to some convenient scale, for example, with 1 cm corresponding to 10 rev/min. Then we establish a direction for the vector 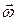by using a right-hand rule, as Fig. 11-6c shows: Curl your right hand about the rotating record, your fingers I pointing in the direction of rotation. Your extended thumb will then point in the direction of the angular velocity vector. If the record were to rotate in the opposite sense, the right-hand rule would tell you that the angular velocity vector then points in the opposite direction.

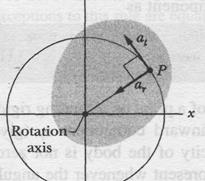
It is not easy to get used to representing angular quantities as vectors. We instinctively expect that something should be moving along the direction of a vector. That is not the case here. Instead, something (the rigid body) is rotating around the direction of the vector. In the world of pure rotation, a vector defines an axis of rotation, not a direction in which something moves. Nonetheless, the vector also defines the motion. The angular acceleration 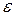is another vector, and it too obeys those rules.

11-5 Relating the Linear and Angular Variables

In Section 4-7, we discussed uniform circular motion, in which a particle travels at constant linear speed 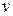along a circle and around an axis of rotation. When a rigid body, such as a merry-go-round, rotates around an axis, each particle in the body moves in its own circle around that axis. Since the body is rigid, all the particles make one revolution in the same amount of time; that is, they all have the same angular speed .

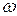However, the farther a particle is from the axis, the greater the circumference of its circle is, and so the faster its linear speed 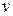must be. You can notice this on a merry-go-round. You turn with the same angular speed 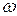regardless of your distance from the center, but your linear speed 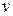increases noticeably if you move to the outside edge of the merry-go-round.

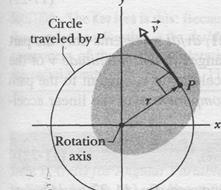
We often need to relate the linear variables , , 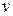and 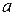for a particular point in a rotating body to the angular variables 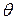, , 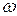and 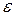for that body. The two sets of variables are related by 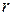, the perpendicular distance of the point from the rotation axis. This perpendicular distance is the distance between the point and the rotation axis, measured along a perpendicular to the axis. It is also the radius 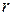of the circle traveled by the point around the axis of rotation.

The Position

If a reference line on a rigid body rotates through an angle 0, a point within the body at a position 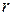from the rotation axis moves a distance along a circular arc, where is given by Eq. 11-1:

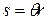(radian measure). 11-17

This is the first of our linear-angular relations. Caution: The angle 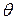here must be measured in radians because Eq. 11-17 is itself the definition of angular measure in radians.