Angular Position

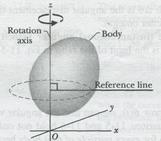Figure 11-2

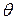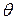Figure 11-2 shows a reference line, fixed in the body, perpendicular to the rotation axis, and rotating with the body. The angular positionof this line is the angle of the line relative to a fixed direction, which we take as the zero angularposition. In Fig. 11-3, the angular position is measured relative to the positive direction of the axis. From geometry, we know that is

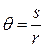
Here is the length of arc (or the arc distance) along a circle and between the axis (the zero angular position) and the reference line; 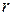is the radius of that circle.

An angle defined in this way is measured in radians(rad) rather than in revolutions (rev) or degrees. The radian, being the ratio of two lengths, is a pure number and thus has no dimension. Because the circumference of a circle of radiu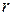s is 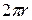, there are 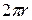radians in a complete circle:

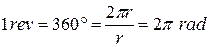
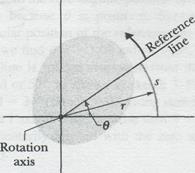Fig. 11-3

and thus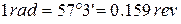

We do not reset 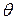to zero with each complete rotation of the reference line about the rotation axis. If the reference line completes two revolutions from the zero angular position, then the angular position 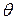of the line is

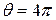rad.

For pure translational motion along the direction, we can know all there is to know about a moving body if we are given 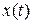, its position as a function of time. Similarly, for pure rotation, we can know all there is to know about a rotating body if we are given 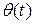, the angular position of the body's reference line as a function of time.