Angular Velocity
Suppose (see Fig. 11-4) that our rotating body is at angular position 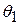 at time
at time  and at angular position
and at angular position 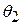 at time
at time 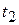 . We define the average angularvelocityof the body in the time interval
. We define the average angularvelocityof the body in the time interval  from
from  to
to 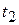 to be
to be
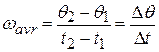 11 -5
11 -5
in which 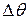 is the angular displacement that occurs during
is the angular displacement that occurs during  (
( 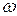 is the lowercase Greek letter omega).
is the lowercase Greek letter omega).
The (instantaneous) angular velocity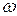 , with which we shall be most concemed, is the limit of the ratio in Eq. 11 -5 as
, with which we shall be most concemed, is the limit of the ratio in Eq. 11 -5 as  approaches zero. Thus,
approaches zero. Thus,
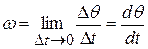 11 -6
11 -6


 If we know
If we know 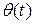 , we can find the angular velocity
, we can find the angular velocity 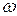 by differentiation.
by differentiation.
 Fig. 11-4
Fig. 11-4
|
Equations 11-5 and 11-6 hold not only for the rotating rigid body as a whole but also for every particle of that body because the particles are all locked together. The unit of angular velocity is commonly the radian per second (rad/s) or the revolution per second (rev/s).
If a particle moves in translation along an  axis, its linear velocity
axis, its linear velocity 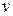 is either positive or negative, depending on whether the particle is moving in the positive or negative direction of the axis. Similarly, the angular velocity
is either positive or negative, depending on whether the particle is moving in the positive or negative direction of the axis. Similarly, the angular velocity 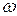 of a rotating rigid body is either positive or negative, depending on whether the body is rotating counterclockwise (positive) or clockwise (negative). The magnitude of an angular velocity is called the angular speed,which is also represented with
of a rotating rigid body is either positive or negative, depending on whether the body is rotating counterclockwise (positive) or clockwise (negative). The magnitude of an angular velocity is called the angular speed,which is also represented with 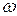 .
.
Дата добавления: 2015-06-17; просмотров: 657;
