Нагрузки действующие на летательный аппарат в полете.
Силы действующие на летательный аппарат делятся на два типа – поверхностные и массовые. В первым относятся аэродинамические нагрузки, тяга двигателей, нагрузки от органов управления, различные силы реакции (подвески, опоры шасси и так далее). Массовые силы – это сила тяжести и силы инерции действующие по всему объему аппарата.
Определение нагрузок на летательный аппарат является сложной и трудоемкой задачей. Различные регламентирующие документы, такие как «Нормы прочности военных самолетов», АП-23 или АП-25 существенно облегчают задачу определения нагрузок, так как включают в себя рекомендации и методики по определению и нормированию нагрузок действующих на летательный аппарат.
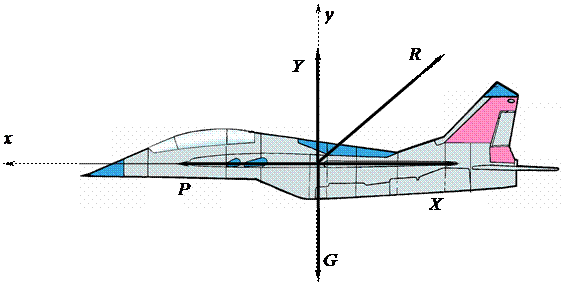 В горизонтальном прямолинейном полете на самолет действуют тяга двигателя P, подъемная сила Y, лобовое сопротивление X и вес летательного аппарата G.
В горизонтальном прямолинейном полете на самолет действуют тяга двигателя P, подъемная сила Y, лобовое сопротивление X и вес летательного аппарата G.
Подъемная сила и лобовое сопротивление выражается через аэродинамические коэффициенты:
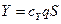 ,
,
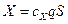 ,
,
где
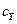 – коэффициент подъемной силы;
– коэффициент подъемной силы;
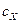 – коэффициент лобового сопротивления;
– коэффициент лобового сопротивления;
S – площадь крыла;
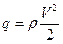 – скоростной напор, где в свою очередь
– скоростной напор, где в свою очередь
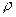 – плотность;
– плотность;
V – скорость полета.
При установившемся горизонтальном полете получим равенства:
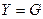 ,
,
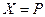 .
.
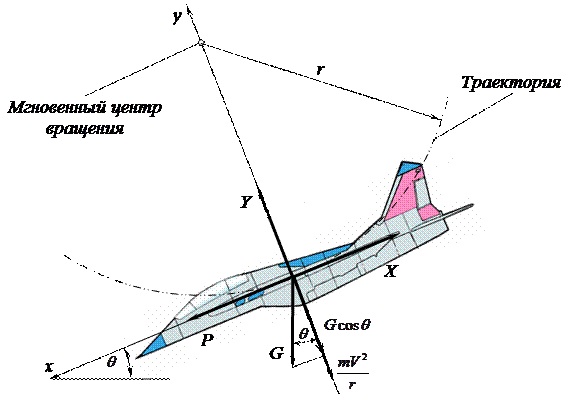 Во всех прочих случаях движение будет либо криволинейным, либо неравномерным. При криволинейном движении в вертикальной плоскости получим:
Во всех прочих случаях движение будет либо криволинейным, либо неравномерным. При криволинейном движении в вертикальной плоскости получим:
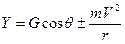 , где
, где
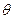 – угол наклона траектории летательного аппарата к горизонту;
– угол наклона траектории летательного аппарата к горизонту;
m – масса летательного аппарата;
r – радиус кривизны траектории.
На практике используется понятие перегрузки – отношение равнодействующих всех поверхностных сил к весу:
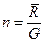 .
.
Обычно используют компоненты перегрузки разложенные по осям летательного аппарата –  ,
, 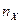 и
и 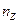 .
.
Необходимо также учитывать угловые скорости и ускорения вращательного движения аппарата вокруг центра тяжести. Так например при маневре в вертикальной плоскости совершаемом с угловым ускорением 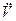 перегрузка агрегата отстоящего от центра тяжести на расстоянии
перегрузка агрегата отстоящего от центра тяжести на расстоянии  будет равна:
будет равна:
 .
.
В горизонтальном прямолинейном полете перегрузка будет равна единице, а ее отклонение от единицы возможно по двум причинам – в результате маневрирования или при попадании в воздушные течения. Поэтому перегрузки делятся на маневренные перегрузки и перегрузки при полете в неспокойном воздухе.
Максимальные маневренные перегрузки достигаются при маневрах в вертикальной плоскости. Величина перегрузки определяется подъемной силой
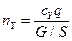
Предельное значение перегрузки может быть определено как
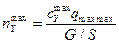 , где
, где
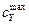 – максимально допустимое значение коэффициента подъемной силы, при котором возможна балансировка и исключается сваливание летательного аппарата;
– максимально допустимое значение коэффициента подъемной силы, при котором возможна балансировка и исключается сваливание летательного аппарата;
 – предельно допустимый скоростной напор.
– предельно допустимый скоростной напор.
При предельных скоростях полета на малых высотах значение вертикальной перегрузки теоретически может достигать значений 15 – 20 единиц. Однако создание самолета обеспечивающего прочность для таких перегрузок экономически невыгодно, тем более что такие перегрузки находятся за пределами выносливости летчика. Поэтому максимальные перегрузки 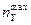 нормируются нормами прочности в зависимости от класса самолета.
нормируются нормами прочности в зависимости от класса самолета.
При полете в неспокойном воздухе появление дополнительных перегрузок объясняется изменением величины и направления скорости полета 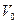 под воздействием порыва имеющего скорость
под воздействием порыва имеющего скорость  . Основное влияние при этом оказывает изменение вектора скорости и, как следствие, угла атаки
. Основное влияние при этом оказывает изменение вектора скорости и, как следствие, угла атаки 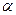 на величину
на величину 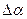 .
.
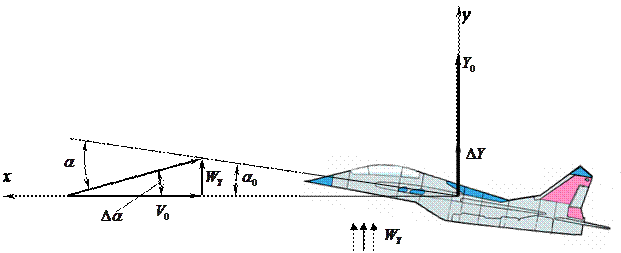 При воздействии вертикального порыва
При воздействии вертикального порыва  изменяется скорость набегающего потока
изменяется скорость набегающего потока
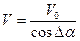
и происходит приращение угла атаки 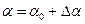 , сопровождаемое изменением подъемной силы
, сопровождаемое изменением подъемной силы
 , где
, где
 – тангенса угла наклона кривой
– тангенса угла наклона кривой 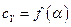 .
.
Ввиду малости угла 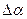 можно принять
можно принять 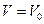 и
и  . Тогда дополнительная перегрузка определится по формуле:
. Тогда дополнительная перегрузка определится по формуле:
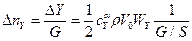 .
.
Данная формула предполагает, что порыв воздуха является резким и мгновенным, в действительности же порывы воздуха имеют свою структуру – скорость порыва постепенно возрастает, достигает максимума, затем постепенно уменьшается до нуля.
 Все это приводит к тому, что прирост перегрузки не столь велик. Структура порыва учитывается введением коэффициента уменьшения перегрузки.
Все это приводит к тому, что прирост перегрузки не столь велик. Структура порыва учитывается введением коэффициента уменьшения перегрузки.
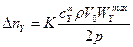 , где
, где
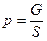 – удельная нагрузка на крыло;
– удельная нагрузка на крыло;
 ;
;
 .
.
Чтобы воспользоваться данными формулами необходимо знать длину 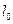 градиентного участка порыва, которая как правило неизвестна. Поэтому для вычисления перегрузок и скоростей порыва используются значения
градиентного участка порыва, которая как правило неизвестна. Поэтому для вычисления перегрузок и скоростей порыва используются значения  , вычисленные для условного стандартного градиентного участка
, вычисленные для условного стандартного градиентного участка 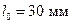 .
.
Величина W вычисленная таким образом называется эффективной скоростью порыва
 , где
, где
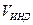 – индикаторная скорость связанная с истинной скоростью
– индикаторная скорость связанная с истинной скоростью 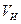 соотношением
соотношением  ;
;
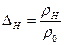 – относительная плотность на высоте H.
– относительная плотность на высоте H.
Статистические данные полученные на множестве самолетов показывают, что значения эффективной скорости порыва укладываются в диапазон ограниченный кривыми
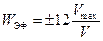 , где
, где
. 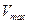 – максимальная скорость полета.
– максимальная скорость полета.
В нормах прочности самолеты делятся на три класса: класс А – маневренные; класс Б – ограниченно маневренные; класс В – неманевренные. Для каждого класса, с учетом назначения, полетного веса и скорости полета задаются значения маневренных перегрузок. Учитываются различные варианты полетного веса, задаются несколько характерных скоростей.
В полете возможен достаточно широкий диапазон сочетания исходных параметров нагружения (перегрузка, скорость, вес). Все разнообразие нагрузок, действующих в полете, сводится к нескольким расчетным случаям, соответствующим наиболее тяжелым условиям нагружения.
При совершении самолетом маневров в воздухе его перегрузка может изменяться от 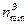 до
до 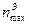 , а скоростной напор от
, а скоростной напор от 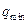 до
до  , где
, где
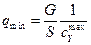 ,
,
 а величина
а величина  соответствует предельно допустимой скорости пикирования.
соответствует предельно допустимой скорости пикирования.
Для крыла как наиболее нагруженного агрегата конструкции зона наиболее нагруженных сочетаний 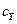 ,
, 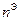 и q разбивается на четыре области:
и q разбивается на четыре области:
Область I
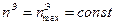 ;
; 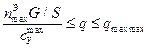
Область II
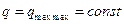 ;
; 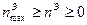 .
.
Область III
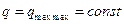 ;
; 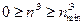 .
.
Область IV
 ;
;  .
.
Наиболее характерные точки всех четырех областей заданы в нормах прочности в качестве расчетных случаев.
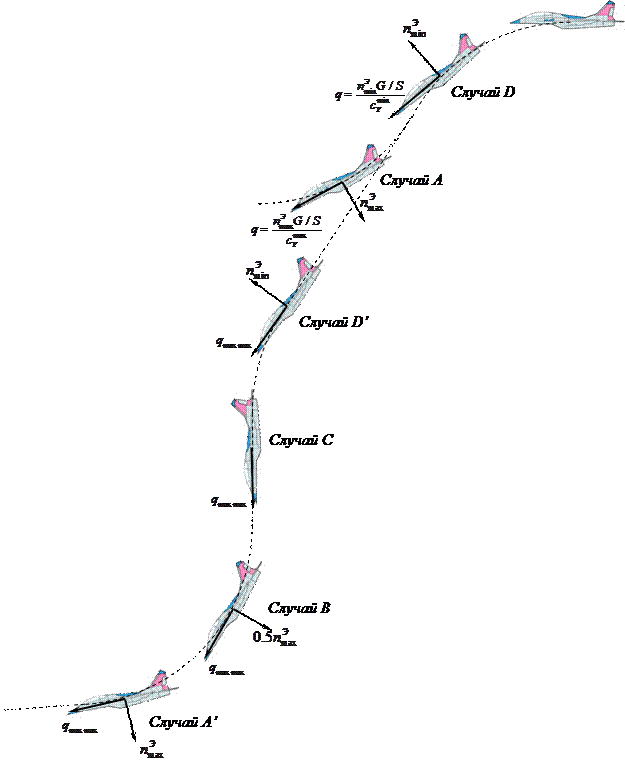 Каждый расчетный случай характеризуется помимо нагрузки формой распределения нагрузки вдоль крыла и вдоль хорды. Распределение нагрузки (давления) вдоль хорды зависит от скорости полета, угла атаки, формой профиля. Распределение давления вдоль крыла и вдоль хорды можно получить на основе методик норм прочности, но более точные данные получаются по результатам продувок геометрически подобных моделей в аэродинамических трубах.
Каждый расчетный случай характеризуется помимо нагрузки формой распределения нагрузки вдоль крыла и вдоль хорды. Распределение нагрузки (давления) вдоль хорды зависит от скорости полета, угла атаки, формой профиля. Распределение давления вдоль крыла и вдоль хорды можно получить на основе методик норм прочности, но более точные данные получаются по результатам продувок геометрически подобных моделей в аэродинамических трубах.
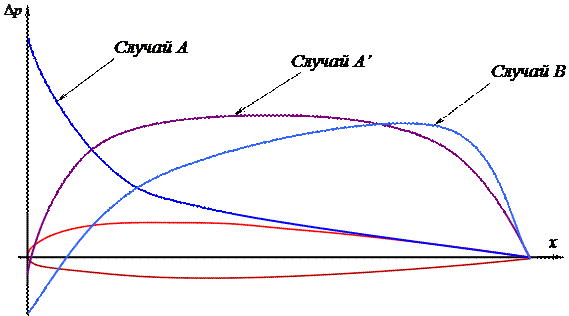 Как видно, в случае нагружения A более всего нагружается носок профиля, хвостовая часть профиля более всего нагружается в случае B, и средняя часть профиля наиболее нагружена в случае нагружения A’.
Как видно, в случае нагружения A более всего нагружается носок профиля, хвостовая часть профиля более всего нагружается в случае B, и средняя часть профиля наиболее нагружена в случае нагружения A’.
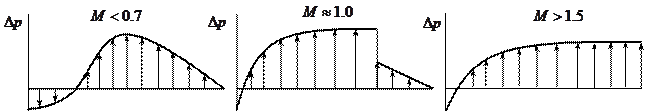 При переходе от дозвуковых к сверхзвуковым скоростям центр давления смещается от носка профиля к его хвосту и происходит выравнивание аэродинамической нагрузки по хорде.
При переходе от дозвуковых к сверхзвуковым скоростям центр давления смещается от носка профиля к его хвосту и происходит выравнивание аэродинамической нагрузки по хорде.
В самолетостроении принят метод расчета по расчетным нагрузкам. Особенность метода состоит в том, что параметры конструкции (толщины, площади) выбираются таким образом, чтобы конструкция выдерживала без разрушения определенную нормами нагрузку. Эта нагрузка называется расчетной нагрузкой 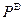 . Расчетная нагрузка равна эксплуатационной умноженной на коэффициент безопасности f:
. Расчетная нагрузка равна эксплуатационной умноженной на коэффициент безопасности f:
 .
.
Аналогично, через коэффициент безопасности можно выразить и перегрузку:
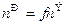 .
.
Коэффициент безопасности применяется во всех областях техники. От его величины зависит степень надежности конструкции и ее эффективность. В авиационной технике назначение коэффициента безопасности сводится к следующему:
· обеспечение невозможности появления расчетной перегрузки 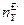 за все время эксплуатации всего парка самолетов данного типа;
за все время эксплуатации всего парка самолетов данного типа;
· обеспечение эксплуатации без накопления остаточных деформаций.
На величину коэффициента безопасности в свою очередь влияют следующие факторы:
· неточность расчетов на фактическую прочность;
· разброс свойств конструкционных материалов;
· точность соблюдения технологии изготовления конструкции.
Эти факторы сводятся к минимуму, соответственно, проведением натурных статических испытаний опытного образца, применением высококачественных материалов и тщательный их контроль, проведением контрольных испытаний серийных летательных аппаратов. Вследствие этого коэффициент безопасности в авиации имеет наименьшее значение по сравнению с другими областями машиностроения и в большинстве расчетных случаев устанавливается равным 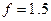 .
.
Дата добавления: 2015-06-17; просмотров: 10757;
