Учет граничных условий
Разрешающее уравнение МКЭ нельзя сразу решить относительно перемещений u. Причина в том, что при его составлении не учтены граничные условия закрепления сооружения в опорах. Поэтому матрица жесткости K является вырожденной (т.е. ее определитель равняется нулю). Чтобы выйти из положения, вектор перемещений приходится делить на две части – на перемещения по закрепленным (з) и незакрепленным (н) направлениям:
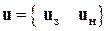 .
.
Так как опоры сооружения обычно бывают достаточно жесткими, их перемещения можно принять равными нулю ( 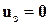 ), а нагрузку, приходящуюся на опоры, не учитывать. В таком случае разрешающее уравнение преобразуется в уравнение меньшего размера. Однако такая процедура существенно меняет структуру матрицы жесткости K и усложняет дальнейшее решение.
), а нагрузку, приходящуюся на опоры, не учитывать. В таком случае разрешающее уравнение преобразуется в уравнение меньшего размера. Однако такая процедура существенно меняет структуру матрицы жесткости K и усложняет дальнейшее решение.
Поэтому используется другой прием: все элементы строк и столбцов матрицы жесткости, соответствующие закреплениям, приравниваются нулю, и лишь вместо их диагональных элементов ставятся единицы. В таком случае разрешающее уравнение упрощается без нарушения ее структуры и принимает вид:
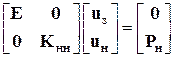 .
.
Здесь E − единичная матрица, 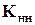 и
и 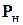 − блоки матрицы жесткости и вектора нагрузки, соответствующие незакрепленным направлениям.
− блоки матрицы жесткости и вектора нагрузки, соответствующие незакрепленным направлениям.
Дата добавления: 2015-06-17; просмотров: 841;
