Закон Кулона. Рисунок 1.3 – Взаимодействие двух зарядов
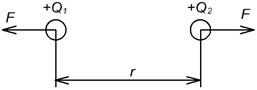
Рисунок 1.3 – Взаимодействие двух зарядов
Сила взаимодействия двух точечных зарядов расположенных в диэлектрической среде прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними, зависит от среды:
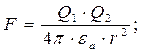где: 1.3
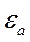- абсолютная диэлектрическая проницаемость.
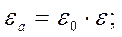1.4
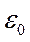- диэлектрическая проницаемость вакуума (электрическая постоянная)
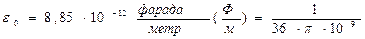
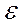- относительная диэлектрическая проницаемость – показывает во сколько раз сила взаимодействия в данной среде меньше, чем в вакууме.
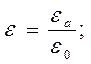1.5
Подставив закон Кулона (1.3) в формулу напряженности (1.2) получим: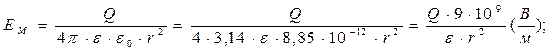 
1.6
Пример1: Два точечных заряда (Q1=2*10-9 Кл, Q2=4*10-9 Кл) расположены в среде с относительной диэлектрической проницаемостью 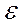=1, на расстоянии 2r друг от друга (r=10 см), определить напряженность электрического поля в точках M и N.
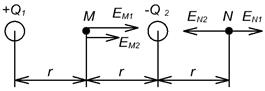
Рисунок 1.4 – Взаимодействие двух зарядов
Для определения напряженности в точке M нужно сложить вектора напряженностей создаваемых первым и вторым зарядом.
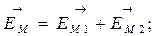
Так как вектора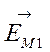 
и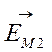 
направлены в одну сторону, для получения EM нужно сложить напряженности EM1 и EM2
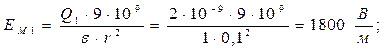
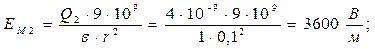
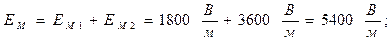
Для определения напряженности в точке N нужно сложить вектора напряженностей создаваемых первым и вторым зарядом.
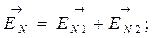
Так как вектора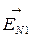 
и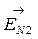 
направлены в противоположные стороны, для получения EN нужно вычесть напряженности EN1 и EN2
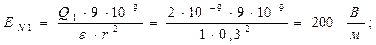
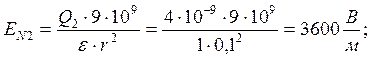
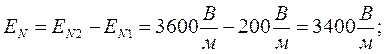
Пример2: Три точечных заряда (Q1=Q2=Q3=0,6*10-6 Кл) расположены в среде с относительной диэлектрической проницаемостью 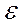=1, в вершинах прямоугольного треугольника, одна сторона которого (r=20 см), α1=60ْ , α2=30ْ определить силы действующие на каждый заряд.
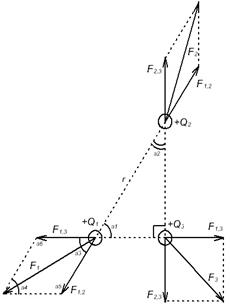
Рисунок 1.5 – Взаимодействие трех зарядов
Для нахождения силы действующей на каждый заряд (F1, F2, F3) нужно найти силы взаимодействия между каждыми двумя зарядами (F1,2, F2,3, F1,3), так как все заряды положительные, то вектора сил взаимодействия будут направлены от зарядов. На каждый заряд будет действовать по две силы. Для их нахождения используем закон Кулона:
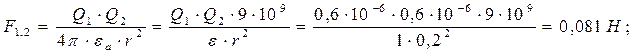
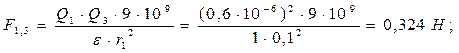
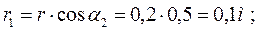
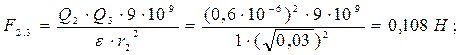
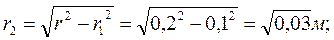
Для определения результирующих сил нужно сложить вектора сил, действующих на каждый заряд:
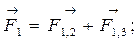
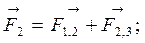
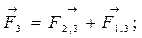
Вектора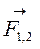 
и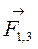 
расположены под углом α3 =α1, для нахождения результирующего вектора достроим вектора до параллелограмма. Угол α4 будет равен углу α5, угол α5 определяется по формуле:
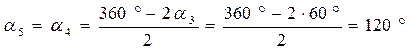
Для определения F1 воспользуемся теоремой косинусов:
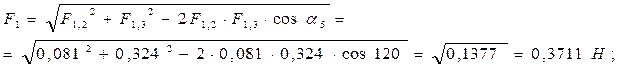
Силы F2 и F3 находятся аналогично:
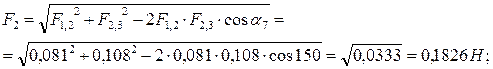
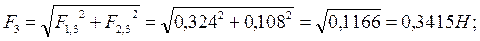
Дата добавления: 2015-06-17; просмотров: 1708;