Применение первого начала термодинамики к изопроцессам. Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния

Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.

– Изохорный процесс (V= const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис.7.3), где процесс 2-1есть изохорное нагревание, а 1-3– изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.

δА = pdV = 0 (7.17)

Из первого начала термодинамикидля изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: δQ=dU.

Согласно формуле (7.12),

dU_m=C_VdT.

Тогда для произвольной массы газа получим

dQ=dU= 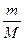C_VdT. (7.18)

– Изобарный процесс (р=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, параллельной оси V. При изобарном процессе работа газа при увеличении объема от V₁ до V₂равна

Рис.7.3 Рис.7.4

A= 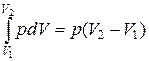(7.19)

и определяется площадью заштрихованного прямоугольника (рис.7.7).

Если использовать уравнение Клапейрона — Менделеева для выбранных нами двух состояний, то

pV₁=νRT₁, pV₂=νRT₂,

откуда

V₂–V₁= ν 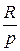(T₂–T₁).

Тогда выражение для работы изобарного расширения примет вид

A=νR(Т₂-Т₁)(7.20)

Из этого выражения вытекает физический смысл молярной газовой постоянной R: если (Т₂–Т₁) = 1 К, то для 1 моль газа R=A,т. е. R численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на 1 К.

В изобарном процессе при сообщении газу массой т количества теплоты

dQ= 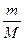C_pdT,

его внутренняя энергия возрастает на величину

dU= 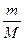C_VdT.

При этом газ совершит работу, определяемую выражением (7.20).

Изотермический процесс (Т=const). Изотермический процесс описывается законом Бойля-Мариотта:

pV= const.

Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу. Найдем работу изотермического расширения газа:

.

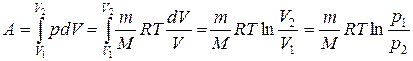Так как при T=const внутренняя энергия идеального газа не изменяется:

dU= 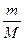C_VdT=0,

то из первого начала термодинамики (δQ=dU+δΑ)следует, что для изотермического процесса

δQ=δΑ,

т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:

Q = 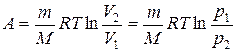(7.21)

Следовательно, для того чтобы при расширении газа температура не понижалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.

Адиабатический процесс. Адиабатическим называется процесс, при котором отсутствует теплообмен (δQ=0) между системой и окружающей средой.

К адиабатическим процессам можно отнести все быстропротекающие процессы. Например, адиабатическим процессом можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д. Из первого начала термодинамики для адиабатического процесса следует, что

δQ= – dU,(7.22)

т. е. внешняя работа совершается за счет изменения внутренней энергии системы.

Используя выражения (7.21) и (7.22), для произвольной массы газа перепишем уравнение в виде

pdV=–νC_VdT. (7.23)

Продифференцировав уравнение состояния для идеального газа pV=ν RT, получим

pdV + Vdp = νRdT. (7.24)

Исключим температуру Т

.

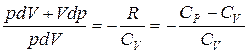Разделив переменные и учитывая, что Ср/С_V =γ, найдем

dp/p= – γdV/V.

Интегрируя это уравнение в пределах от р₁до p₂ соответственно от V₁до V₂а затем потенцируя, придем к выражению

p₂/p₁=(V₁/V₂)^γ,

или p₁ 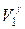=p₂ .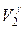

Так как состояния 1 и 2выбраны произвольно, то можно записать

pV^γ=const. (7.25)

Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

Для перехода к переменным Т, V или p,Т исключим из (7.27) с помощью уравнения Клапейрона - Менделеева соответственно давление или объем:

TV ^γ–1=const, (7.26)

T^γp^1–γ=const. (7.27)

Выражения (7.26) – (7.27) представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина

γ =C_p/C_V= (i+2)/i, (7.28)

называется показателем адиабаты. Для одноатомных газов (Ne, Не и др.), достаточно хорошо удовлетворяющих условию идеальности, i=3, γ = 1,67. Для двухатомных газов (Н₂, N₂, О₂ и др.) i=5, γ= 1,4. Значения γ, вычисленные по формуле (7.28), хорошо подтверждаются экспериментом.

Диаграмма адиабатического процесса (адиабата) в координатах p, V изображается гиперболой (рис.7.5).

На рисунке видно, что адиабата (pV^γ=const) более крута, чем изотерма (pV=const). Это объясняется тем, что при адиабатическом сжатии 1-3увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.

Вычислим работу, совершаемую газом в адиабатическом процессе. Запишем:

δА=–νC_VdT.

Если газ адиабатически расширяется от объема V₁до V₂,то его температура уменьшается от Τ₁до Т₂и работа расширения идеального газа

A= 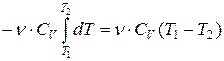. (7.29)

Применяя те же приемы, что и при выводе формулы (7.25), выражение (7.29) для работы при адиабатическом расширении можно преобразовать к виду

A= 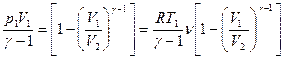. (7.30)

Работа, совершаемая газом при адиабатическом расширении 1–2 (определяется площадью, заштрихованной на рис.7.5, меньше, чем при изотермическом. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом – температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

Рассмотренные изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность – они происходят при постоянной теплоемкости.