Уравнение Бернулли и следствия из него

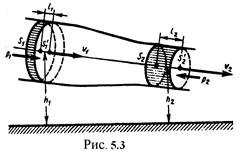Выделим в стационарно текущей идеальной жидкости трубку тока, ограниченную сечениями S₁и S₂, по которой слева направо течет жидкость (рис. 5.3). Пусть в месте сечения S₁ скорость течения v₁, давление р₁и высота, на которой это сечение расположено, h₁. Аналогично, в месте сечения S₂скорость течения v₂, давление p₂ и высота сечения h₂. За малый промежуток времени Δt жидкость перемещается от сечений S₁ и S₂ к сечениям S′₁ и S′₂.

Согласно закону сохранения энергии, изменение полной энергии W₂– W₁ идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемеще­нию массы т жидкости:

W₂– W₁= A, (5.3)

где W₁и W₂ - полные энергии жидкости массой т в местах сечений S₁и S₂соответственно.

С другой стороны, А - это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S₁и S₂,за рассматриваемый малый промежуток времени Δt. Для перенесения массы т от S₁ до S'₁жидкость должна переме­ститься на расстояние l₁ = υ₁Δt и от S₂ до S'₂- на расстояние l₂ = υ₂Δt. Отметим, что l₁и l₂настолько малы, что всем точкам объемов, закрашенных на рис.6.3, приписывают постоянные значения скорости υ, давления р и высоты h. Следовательно,

А = F₁l₁ + F₂l₂ (5.4)

где F₁ = p₁S₁и F₂ = - p₂S₂ (отрицательна, так как направлена в сторону, противопо­ложную течению жидкости; рис.5.3).

Полные энергии W₁и W₂будут складываться из кинетической и потенциальной энергий массы т жидкости:

W₁ = mυ₁²/2 + mgh₁, (5.5)

W₂= mυ₂²/2 + mgh₂(5.6)

Подставляя (5.5) и (5.6) в (5.3) и приравнивая (5.3) и (5.4), получим

mυ₁²/2 + mgh₁ + p₁S₁υ₁Δt = mυ₂²/2 + mgh₂ + p₂S₂υ₂Δt (5.7)

Согласно уравнению неразрывности для несжимаемой жидкости (5.2), объем, занимаемый жидкостью, остается посто­янным, т. е. ΔV = S₁υ₁Δt = S₂υ₂Δt. Разделив выражение (5.5) на ΔV, по­лучим ρυ₁²/2 + ρgh₁ + p₁ = ρυ₂²/2 + ρgh₂ + p₂, где ρ - плотность жидкости. Но так как сечения выбирались произвольно, то мо­жем записать

ρυ²/2 + ρgh + p = const (5.8)

Выражение (5.8) называется уравнением Бернулли.Как видно из его вывода, уравнение Бернулли – выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Оно хорошо выполняется и для реальных жидкостей, внутреннее трение которых не очень велико.

Величина р в формуле (5.8) называется статическим давлением(давление жидкости на поверхность обтекаемого ею тела), величина ρυ²/2 – динамическим давлением.Как уже указывалось выше, величина ρgh представляет гидростатическое давление.

Для горизонтальной трубки тока (h₁= h₂) выражение (5.8) принимает вид

ρυ²/2 + p = const, (5.9)

где p + ρυ²/2называется полным давлением.

Из уравнения Бернулли (5.9) для горизонтальной трубки тока и уравнения неразрывности (5.2) следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно продемонстрировать, установив вдоль трубы 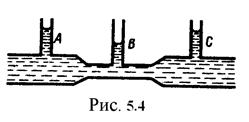ряд манометров(рис.5.4). В соответствии с уравнением Бернулли опыт показывает, что в манометрической трубке В, прикрепленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.

Так как динамическое давление связано со скоростью движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого применяется трубка Пито - Прандтля (рис.5.5).

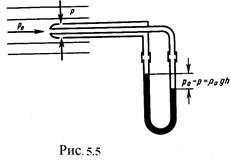Прибор состоит из двух изогнутых под прямым углом трубок, про­тивоположные концы которых присоедине­ны к манометру. С помощью одной из трубок измеряется полное давление (р₀), с помощью другой - статическое (р). Ма­нометром измеряется разность давлений:

р₀ – p = ρ₀gh, (5.10)

где ρ₀– плотность жидкости в манометре.

С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давлению:

р₀ – p = ρυ²/2(5.11)

Из формул (5.10) и (5.11) получаем иско­мую скорость потока жидкости:

υ = 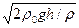(5.12)

Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса(рис.5.6).

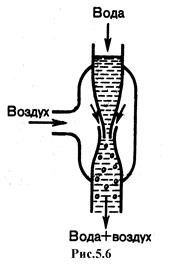Струя воды подается в трубку, открытую в атмосферу, так что давление на выходе из трубки равно атмосферному. В трубке имеется сужение, по которому вода течет с большей скоростью. В этом месте давление меньше атмосферного. Это давление устанавливается и в откачанном сосуде, который связан с трубкой через разрыв, имеющийся в ее узкой части. Воздух увлекается вытекающей с большой скоростью водой из узкого конца. Таким образом можно откачивать воздух из сосуда до давления 100 мм.рт.ст.

Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие (рис.5.7).

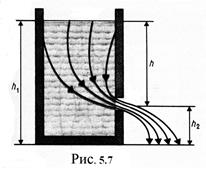Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде на уровне h₂ выхода ее из отверстия). Напишем для них уравнение Бернулли:

ρυ₁²/2 + ρgh₁ + p₁ = ρυ₂²/2 + ρgh₂ + p₂.

Так как давления р₁и р₂в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. p₁ = p_2, то уравнение будет иметь вид
υ₁²/2 + gh₁ = υ₂²/2 + gh₂.

Из уравнения неразрывности (5.2) следует, что υ₂/υ₁ =S₁/S₂, где S₁и S₂ - площа­ди поперечных сечений сосуда и отверстия. Если S₁>> S₂, то членом υ₁²/2 можно пренебречь и

υ₂²= 2g(h₁ – h₂) = 2gh,

υ₂ = 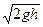(5.13)

Это выражение получило название формулы Торричелли.