Законы сохранения импульса и энергии

Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной).

Для замкнутой системы в случае отсутствия внешних сил получим

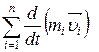= =0, т.е.

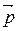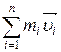= =const. (3.14)

Это выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени.

Закон сохранения импульса представляет собой один из фундаментальных законов природы и проявляется в целом ряде явлений. В частности, он лежит в основе реактивного движения, проявляется в процессе соударения тел.

Для вывода закона сохранения энергии рассмотрим уравнения

m₁ = + + ,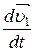

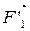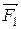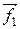m₁ = + + ,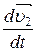

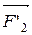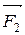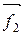m_n = + + .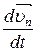

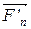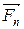Здесь 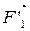, , 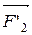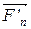- равнодействующие внутренних консервативных сил; 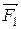, , 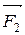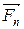- равнодействующие внешних консервативных сил; 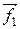, , 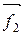- внешние неконсервативные силы.

Двигаясь под действием сил, точки системы за интервал времени dt совершают перемещения, соответственно равные 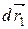, , 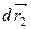..., 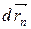. Умножим каждое из уравнений скалярно на соответствующее перемещение и, учитывая, что = 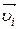dt, получим:

m₁ ,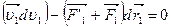

m₂ ,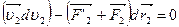

m_n .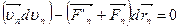

Сложив эти уравнения, получим

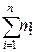
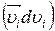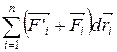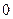– = . (3.15)

Первый член левой части равенства (3.15)

= ,

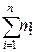
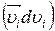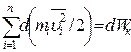где dW_к – есть приращение кинетической энергии системы. Второй член 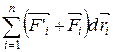равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т.е. равен элементарному приращению потенциальной энергии dW_p системы.

Правая часть равенства (3.15) определяет работу внешних неконсервативных сил, действующих на систему. Таким образом, имеем

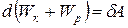. (3.16)

При переходе системы из состояния 1 в какое-либо состояние 2

,

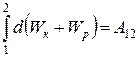т.е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то из (3.15) следует, что

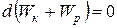, откуда

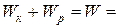const, (3.17)

т.е. полная механическая энергия системы сохраняется постоянной. Выражение (3.17) представляет собой закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т.е. не изменяется со временем.

Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние), называются консервативными системами. Закон сохранения механической энергии можно сформулировать так: в консервативных системах полная механическая энергия сохраняется.

В диссипативных системах механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии.

Из этого следует всеобщий закон сохранения энергии, сформулированный М.В. Ломоносовым: энергия ни откуда не возникает и никуда не исчезает – она переходит из одного вида в другой: из механической в тепловую, электрическую, световую; из тепловой в механическую, электрическую, световую и т.д., или передается от одного тела к другому, но общее ее количество остается постоянным.