Кинетическая и потенциальная энергии

Кинетическая энергия W_к механической системы – это энергия механического движения этой системы.

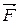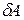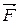Сила , действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа силы на пути, который тело прошло за время возрастания скорости от 0 до 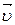, идет на увеличение кинетической энергии dW_к тела, т. е. .

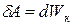Тело массой m, движущееся со скоростью 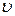, обладает кинетической энергией

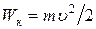. (3.6)

Из формулы (3.6) видно, что кинетическая энергия зависит только от массы и скорости тела, т.е. кинетическая энергия системы есть функция состояния ее движения.

Потенциальная энергия 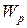– механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

Если в силовом поле работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений, то такие поля называются потенциальными, а силы, действующие в них, – консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной;ее примером является сила трения.

Тело, находясь в потенциальном поле сил, обладает потенциальной энергией 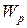. Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:

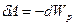. (3.7)

Работа 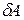выражается как скалярное произведение силы 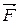на перемещение 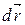и выражение (3.7) можно записать в виде

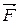
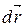
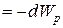. (3.8)

Для консервативных сил

, , ,

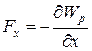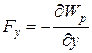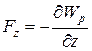или в векторном виде

,

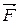
где

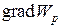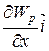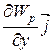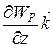= + + (3.9)

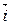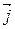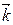( , , – единичные векторы координатных осей). Вектор, определяемый выражением (3.9), называется градиентом скаляра .

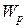Для него наряду с обозначением 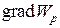применяется также обозначение 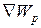. 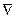(«набла») означает символический вектор, называемый оператором Гамильтона или набла-оператором:

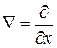
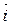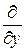
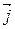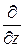
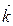+ + . (3.10)

Конкретный вид функции 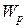зависит от характера силового поля. Например, потенциальная энергия тела массой m, поднятого на высоту h над поверхностью Земли, равна

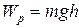, (3.11)

где высота h отсчитывается от нулевого уровня, для которого 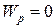. Выражение (3.11) вытекает непосредственно из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты h на поверхность Земли.

Потенциальная энергия упругодеформированного тела (пружины) равна

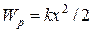. (3.12)

Потенциальная энергия системы, подобно кинетической энергии, является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.

Полная механическая энергия системы – энергия механического движения и взаимодействия:

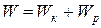, (3.13)

т.е. равна сумме кинетической и потенциальной энергий.