Ускорение.
Движение точки характеризуется также ускорением—быстротой изменения скорости
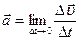 ;
; 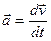
т.е. вектор 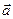 равен производной
равен производной 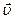 по времени. Направление вектора
по времени. Направление вектора 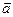 совпадает с направлением приращения скорости
совпадает с направлением приращения скорости 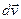 за
за 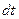 т.к.
т.к. 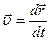 , то ускорение точки равно второй производной по времени от радиус-вектора:
, то ускорение точки равно второй производной по времени от радиус-вектора:
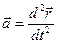 ;
; 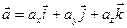 ;
; 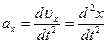 ;
;
где 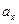 —проекция.
—проекция.
Если траектории точки плоская кривая, то можно выбрать два перпендикулярных направления: касательная к траектории (орт 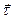 ) и нормали к ней
) и нормали к ней 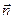 . Тогда
. Тогда 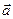 раскладывается по составляющим
раскладывается по составляющим 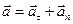 .
.
Т.к. вектор скорости направлен по касательной к траектории в сторону её движения, то
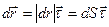 ;
;
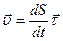 ;
;
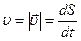 ;
; 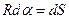
тогда 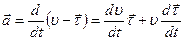 ;
; 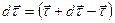 —приращение орта касательной к траектории, соответствующее элементарному пути
—приращение орта касательной к траектории, соответствующее элементарному пути 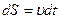 за
за 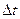 .
.
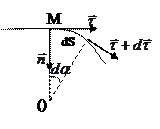 Ввиду малости
Ввиду малости 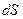 его можно считать совпадающим с дугой окружности радиуса
его можно считать совпадающим с дугой окружности радиуса 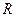 с центром в т.0 с центральным углом
с центром в т.0 с центральным углом 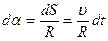 .
.
| |
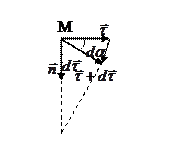 Соответственно, единичный вектор
Соответственно, единичный вектор 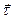 повор. на
повор. на 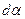 . Из равнобедренного треугольника
. Из равнобедренного треугольника 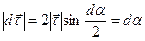 , ввиду малости
, ввиду малости 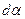 ; по направлению
; по направлению 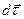 совпадает с
совпадает с 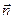 (при
(при 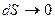
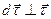 )
)
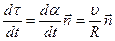 ;
;
и ускорение точки
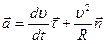 ;
;
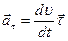 — касательное(тангенциальное) ускорение характеризует быстроту изменения модуля скорости. При ускоренном движении
— касательное(тангенциальное) ускорение характеризует быстроту изменения модуля скорости. При ускоренном движении 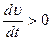 и
и 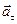 совпадает с
совпадает с 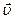 , при замедленном
, при замедленном 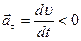 и
и 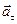 не совпадает с
не совпадает с 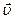 .
.
Нормальное ускорение 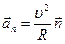 характеризует быстроту изменения направления вектора скорости. Направлено к центру кривизны траектории;
характеризует быстроту изменения направления вектора скорости. Направлено к центру кривизны траектории; 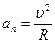 ; поэтому его называют центростремительным. При прямолинейном движении
; поэтому его называют центростремительным. При прямолинейном движении 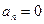 .
.
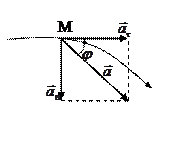 Модуль ускорения
Модуль ускорения
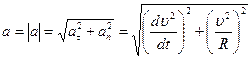 ;
;
При ускоренном движении 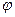 — острый, при замедленном—тупой (
— острый, при замедленном—тупой ( 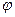 угол между
угол между 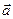 и
и 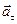 ). Если движение по окружности равномерное
). Если движение по окружности равномерное 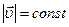 то
то 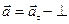 касательной.
касательной.
2.Динамика поступательного движения
2.1. Простейшим видом механического движения твердого тела является поступательное движение. при котором прямая, соединяющая любые две точки тела перемещается вместе с телом, оставаясь || своему первоначальному направлению (шарик на пружине относительно Земли, поршень в цилиндре стационарного двигателя, лифт, резец токарного станка и др.). Траектории всех точек ела известны. Радиус-вектор все точек тела за время 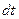 изменяется на одну и туже величину
изменяется на одну и туже величину 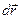 , скорости всех точек и ускорения одинаковы:
, скорости всех точек и ускорения одинаковы:
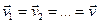 ;
; 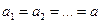
т.е. для описания можно взять одну точку, если 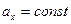 то
то
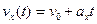
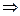
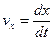
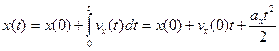
Дата добавления: 2015-06-17; просмотров: 1049;
