ЗАКОН ОМА

Между основными электрическими параметрами цепи, такими, как ток, сопротивление, эдс, напряжение, существует строго определенная связь (рис.13). Эта связь устанавливается законом Ома.

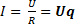(2-12)

т.е. сила тока на участке электрической цепи при постоянной проводимости пропорциональна напряжению.

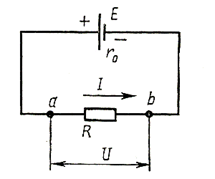
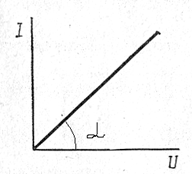
Рис.13 Рис. 14

Зависимость тока от напряжения называют вольтамперной характеристикой (ВАХ) (рис.14). Как следует из выражения(1-12), ВАХ участка цепи при его постоянной проводимости есть линейная функция, т.е. прямая линия, проходящая через начало координат. Причем, ctgα = R= U/I. Ранее приведенную формулу можно представить и так

U = IR, (2-13)

причем, величину равную произведению тока на сопротивление участка цепи, называют падением напряжения на этом участке.

При установлении связи между параметрами, относящимися ко всей цепи, необходимо учитывать сопротивление всей цепи, а также эдс источника, т.е. закон Ома для всей цепи

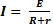,(2-14)

где R - сопротивление внешнего участка цепи, r-сопротивление внутреннего участка цепи. Произведение I r=ΔU называют падением напряжения на внутреннем участке цепи.

5. ЗАКОНЫ КИРХГОФА

Первый закон Кирхгофа - алгебраическая сумма токов, в узловой точке (а или б) (рис.15а) цепи равна нулю,

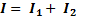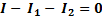или (2-15)

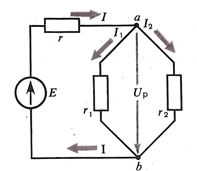
а б

Рис.15

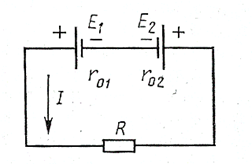
Второй закон – алгебраическая сумма всех действующих эдс в любом контуре электрической цепи равна алгебраической сумме падений напряжений на резисторах, входящих в контур. Для замкнутого контура (рис.15б) второй закон Кирхгофа запишется в виде

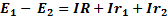(2-16)

Таким образом, закон Ома для всей цепи можно считать частным случаем второго закона Кирхгофа.

Знаки в алгебраической сумме для эдс и падений напряжений следует производить в соответствии со следующими правилами:

1) если направление эдс совпадает с условно выбранным направлением обхода по контуру, то эдс берут со знаком плюс и наоборот;

2) если направление тока на участке цепи совпадает с направлением выбранного обхода контура, то падение напряжения на этом участке берется со знаком плюс и наоборот.