Обратная связь в усилительных устройствах

Современные усилительные элементы обладают значительным разбросом параметров от образца к образцу, температурной нестабильностью и существенной нелинейностью.

Обеспечение высоких технических характеристик усилительных устройств при использовании таких элементов приводит к необходимости применения специальных мер по стабилизации и линеаризации. Этого можно добиться введением в усилитель специальных элементов, зависимость параметров которых от температуры или характер их нелинейности таковы, что позволяют в определенной мере скомпенсировать температурный уход параметров усилительных элементов или их собственную нелинейность. Однако такой метод требует индивидуальной настройки каждого образца усилителя высококвалифицированным специалистом, что нетехнологично, дорого и практически неприемлемо при массовом производстве.

Значительно более эффективным и универсальным методом стабилизации и линеаризации является метод обратной связи.

Идея этого метода заключается в том, что управляющее напряжение усилителя формируется как результат сравнения мгновенного значения входного сигнала с соизмеримой с ним по уровню частью выходного сигнала таким образом, чтобы соответствующим воздействием на усилитель свести к минимуму их отличия. Тем самым происходит автоматическая компенсация всех факторов, приводящих к отличию мгновенных значений входного и выходного сигналов: нелинейных и частотных искажений, собственных шумов, нестабильности параметров усилителя и т. д.

Обобщенная линеаризованная модель усилителя с обратной связью представлена на рис. 5.8, где

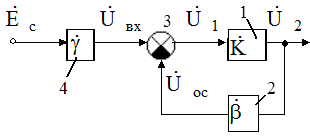Рис. 5.8. Линеаризованная модель усилителя с обратной связью

1 - исходный усилитель с комплексным коэффициентом передачи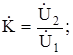

2 - цепь обратной связи с коэффициентом передачи ;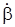

3 - сравнивающее (вычитающее) устройство;

4 - цепь связи источника сигнала с исходным усилителем с коэффициентом передачи .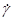

Характерной особенностью усилителя с обратной связью является наличие цепи обратной связи 2, через которую выходной сигнал усилителя подводится во входную (управляющую) цепь, где он вычитается из входного сигнала. Благодаря этому, управляющее напряжение исходного усилителя 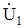несет информацию об отличии выходного напряжения 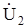от ЭДС входного сигнала :

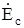(5.1)

где 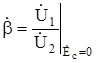- коэффициент передачи выходного напряжения к управляющим зажимам (коэффициент обратной связи);

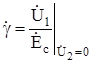- коэффициент передачи ЭДС-сигнала к управляющим зажимам (коэффициент прямой связи).

Сравнение сигналов прямой и обратной связи на рис. 5.8 отражено введением идеального вычитающего устройства 3. Реально вычитание осуществляется либо подачей сравниваемых напряжений одинаковой полярности на противоположные зажимы цепи управления, либо подачей на один и тот же зажим сравниваемых напряжений в разной полярности. Введем понятие комплексного коэффициента усиления ЭДС-сигнала с обратной связью

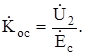(5.2)

Из рассмотрения рис. 5.8 следует очевидное соотношение

. (5.3)

При неограниченном увеличении произведения коэффициента усиления исходного усилителя

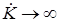
для получения заданного значения выходного напряжения с обратной связью требуется согласно (5.3) управляющее напряжение

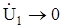
откуда согласно (5.1) следует, что

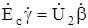
и предельное значение комплексного коэффициента усиления с обратной связью принимае вид

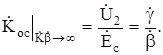(5.4)

Соотношение (5.4) отражает важнейшее свойство обратной связи: в предельном случае усиление усилителя с обратной связью не зависит от параметров исходного усилителя иполностью определяется параметрами цепей прямой и обратной связи.

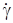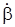Стабильность и линейность пассивных элементов, определяющих значения и , могут быть сделаны значительно более высокими, чем у усилительных элементов, определяющих значение 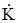. В результате стабильность и линейность усилителя с обратной связью также сказываются более высокими, чем у исходного усилителя.

Ниже будет показано, что стабилизирующие свойства обратной связи проявляются и при конечных значениях произведения 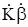, что и объясняет чрезвычайно широкое использование обратной связи при проектировании усилительных устройств.

Определим коэффициент усиления с обратной связью при конечном значении произведения 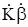по очевидному алгоритму (см. рис. 5.8)

,

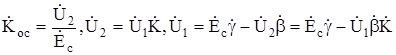откуда 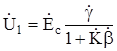(5.5)

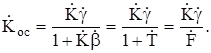и (5.6)

Здесь 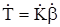- петлевое усиление (усиление по замкнутому кольцу обратной связи); 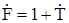- глубина обратной связи.

В предельном случае (при 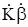®¥) управляющее напряжение при вычитании сигналов прямой и обратной связи стремилось к нулю. В общем случае, то есть при конечном петлевом усилении и векторном вычитании сигналов, признаком стабилизирующей обратной связи является уменьшение амплитуды управляющего напряжения при введении обратной связи, которая определяется из (5.5) по очевидному соотношению

.. .

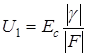Поэтому, если ïFï>1, то обратная связь приводит к уменьшению управляющего напряжения. Обратная связь такого типа называется отрицательной (ООС). При ïFï<1 связь называется положительной (ПОС). Положительная обратная связь оказывает дестабилизирующее действие и поэтому в чистом виде в усилителях практически не применяется.

В силу неравномерности АЧХ исходного усилителя и цепи обратной связи ïFï может быть больше единицы в одном диапазоне частот и меньше единицы - в другом. Другими словами, вид обратной связи (ООС или ПОС) можно установить лишь для определенного диапазона частот.

Поэтому, когда указывается конкретный тип обратной связи, то имеется в виду ее характер лишь в рабочей области частот усилителя.

Представляя (5.6) в показательной форме

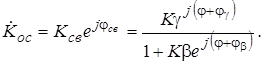
Полагая, что при j®0 cosj » 1, sinj » j из (5.7) и (5.8) можно получить упрощенные соотношения (для идеального g и b):

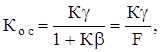(5.7)

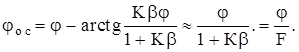(5.8)

Эффект от введения обратной связи можно оценить по изменению значения конкретного параметра усилителя до (b=0) и после ее введения. Тогда из (5.7) и (5.8) следует, что коэффициент усиления и фазовый сдвиг усилителя с обратной связью в F раз меньше, чем у исходного усилителя.

Однако, если уменьшение фазового сдвига является полезным эффектом, то снижение усиления, конечно же, является негативным эффектом от введения ООС, своеобразной “платой” за стабилизацию.

Дифференцируя обе части (5.7) легко получить выражение, подтверждающее стабилизирующие свойства ООС (g = const, b = const):

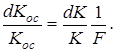(5.9)

Из (5.9) следует, что влияние нестабильности исходного усилителя на нестабильность усилителя с ООС уменьшается в F раз.

При глубокой обратной связи, когда Кb®¥ стабильность усилителя с ООС полностью определяется стабильностью цепей прямой и обратной связи, то есть

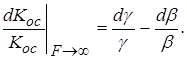
Отсюда следует вывод о необходимости тщательного подбора элементов этих цепей, поскольку именно они определяют потенциальную точность и линейность усилителя с ООС. Из (5.7) легко получить предельное соотношение, аналогичное ранее полученному (5.4), для коэффициента усиления при Кb®¥ (F®¥)

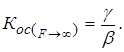(5.10)

Рис. 5.9. Изменение сигналов в системе с ООС при вариации параметров усилителя

Важно подчеркнуть физическую суть стабилизирующего действия ООС. На рис. 5.9 а,б показано распределение напряжений в характерных точках структурной схемы - для упрощения принято g=1 - для двух существенно различных значений усиления исходного усилителя К=90 и К=990.

Как следует из рис. 5.9, изменение усиления исходного усилителя в 11 раз (с 90 до 990), усиление входного сигнала (коэффициент усиления с обратной связью) изменилось в 1.1 раза (с 9 до 9.9). Хорошо видно, что стабилизация усиления входного сигнала достигается за счет изменения в нужную сторону управляющего напряжения.

Количественная оценка влияния ООС на величину всех видов искажений, вносимых усилителем, является достаточно сложной задачей.

Так, например, для оценки изменения уровня шумов при введении ООС необходимо контролировать модуль и фазу петлевого усиления в полосе частот от 0 до ¥, в которой сосредоточена энергия шумов. Определение же уровня нелинейных искажений на основе используемой выше линеаризованной модели усилителя вообще невозможно.

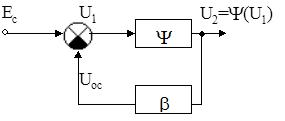Рис. 5.10. Нелинейная модель усилителя с ООС

Линеаризующее действие ООС удобнее проиллюстрировать графически путем построения статической характеристики усилителя с ООС по структурной схеме (рис. 5.10).

Здесь исходный усилитель представлен нелинейной статической характеристикой

U₂=y(U₁),

а управляющее напряжение есть линейная комбинация входного сигнала и сигнала обратной связи

U₁=Е_сg - U₂b,

графически представляемая прямой линией с углом наклона, определяемым значением b. При Е_с=0 эта прямая проходит через начало координат статической характеристики. Изменение значения Е_с приведет к параллельному перемещению этой прямой. Точка пересечения этой прямой со статической характеристикой дает графическое решение уравнения статической характеристики усилителя с обратной связью U₂=y_ос(Е_с).

На рис. 5.11 хорошо видна более высокая линейность статической характеристики усилителя с обратной связью. На основе квазилинейной трактовки показано, что содержание высших гармоник при одинаковом уровне первой гармоники выходного напряжения уменьшается за счет введения ООС в F раз.

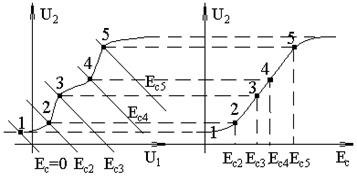Рис. 5.11. Эффект линеаризации характеристики вход-выход при ООС

Для определения влияния ООС на шумовые помехи можно использовать соотношение, полученное на основе структурной схемы рис. 5.12, где источники шумов (e_w1 и e_w2) введены для общности в разные точки исходного усилителя с общим усилением К=К₁К₂.

Легко определить значение шумового напряжения на выходе усилителя с обратной связью U_2ш^ос, вызванное введенными источниками шумов 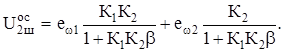Очевидно, что при отсутствии обратной связи (b=0)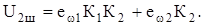

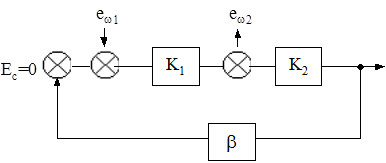Рис. 5.12. Схема для определения влияния шумов при ООС

Откуда следует, что шумовое напряжение на выходе усилителя при введении ООС уменьшается в F раз. Однако, поскольку и усиление полезного сигнала при ООС уменьшается в F раз, отношение сигнал/шум, характеризующее чувствительность усилителя, при ООС не изменяется. Подчеркнем, что эти выводы справедливы лишь для тех спектральных составляющих шумов, для которых фазовый сдвиг петлевого усиления мал. Воспринимая неравномерность АЧХ исходного усилителя как нестабильность усиления последнего, можно считать по аналогии с (5.9), что относительная неравномерность АЧХ усилителя с ООС в F раз меньше, чем у исходного усилителя. Это утверждение также справедливо для ограниченного диапазона частот, где малы фазовые сдвиги петлевого усиления.

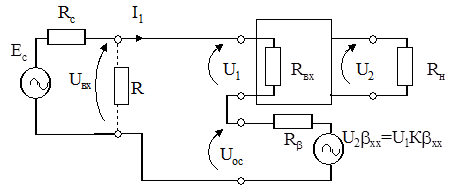Рис. 5.13. Расчетная схема усилителя с последовательной ООС

Влияние обратной связи навходное сопротивление усилителя определяется способом подачи сигнала обратной связи на управляющие зажимы усилителя. Если напряжения сигнала обратной связи и управляющего сигнала включены последовательно друг с другом, то такая связь называется последовательной (рис. 5.13). Здесь цепь обратной связи представляется в виде ЭДС обратной связи U₂b_xx, где 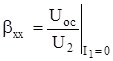, и выходного сопротивления цепи обратной связи R_b. Приведенные ниже соотношения справедливы для малых фазовых сдвигов в петле обратной связи. Входное сопротивление усилителя при ООС (когда мгновенные значения управляющего напряжения U₁ и ЭДС обратной связи имеют одинаковую полярность) по определению равно

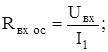
ток во входном контуре равен

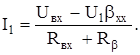
Подставляя сюда значения U₂=U₁K, U₁=I₁R_вх, получим

,

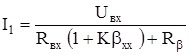откуда

R_{вх ос}=R_вх (1+Kb_хх)+R_b . (5.11)

Входное сопротивление усилителя с последовательной ООС больше, чем у исходного усилителя в F раз.

Физически увеличение входного сопротивления достигается уменьшением входного тока

за счет резкого уменьшения управляющего напряжения при введении ООС.

Если же к входным зажимам усилителя с обратной связью подключено сопротивление, потенциал на зажимах которого не меняется при введении обратной связи (сопротивление R на рис. 5.13), то влияние его на входное сопротивление не зависит от наличия или отсутствия обратной связи.

Так, например, при наличии R даже при бесконечной глубине ООС входное сопротивление не может быть больше, чем R:

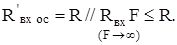
По определению коэффициенты обратной и прямой связи равны:

.

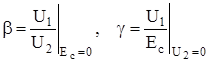Согласно рис. 5.13

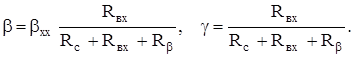(5.12)

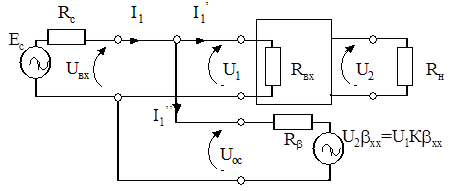Рис. 5.14. расчетная схема усилителя с параллельной обратной связью

Из (5.12) следует, что при последовательной ООС значение b, а следовательно, и глубина обратной связи зависят от значения внутреннего сопротивления источника сигнала R_c. При R_c=¥ (или обрыве входной цепи) последовательная обратная связь исчезает. Это обстоятельство необходимо учитывать при определении параметров усилителя с последовательной ООС. Если сигнал обратной связи подается параллельно управляющим зажимам, то такая связь называется параллельной (рис. 5.14).

Здесь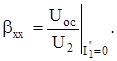

По определению

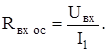
Ток во входной цепи равен сумме тока через управляющие зажимы I₁^’ и тока в цепи обратной связи I₁^’’:

I₁= I₁^’+ I₁^’’.

Для того, чтобы связь была отрицательной, необходимо, чтобы мгновенное значение управляющего напряжения и ЭДС обратной связи были в противофазе, что отражено введением знака «минус» при ЭДС обратной связи. Определим значения токов I₁^’ и I₁^’’:

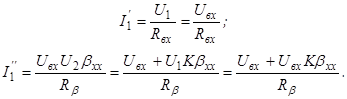
В результате несложных преобразований можно получить

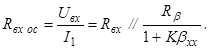(5.13)

Входное сопротивление усилителя с параллельной ООС меньше, чем у исходного усилителя. Очевидно, что при глубокой ООС, когда (1+Кb_хх)®¥, входное сопротивление при параллельной ООС стремится к нулю.

Физически уменьшение входного сопротивления происходит из-за большой величины тока в цепи обратной связи, определяемого высокой разностью потенциалов, приложенных к R_b .

Воспользовавшись уже известным определением

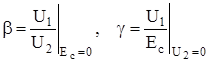
получим значение коэффициента обратной и прямой связи при параллельной ООС

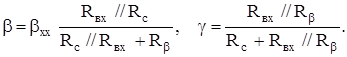(5.14)

Из (5.14) следует, что параллельная ООС исчезает при R_с=0.

На величину выходного сопротивления усилителя влияет способ съема сигнала обратной связи в выходной цепи.

Если напряжение обратной связи пропорционально выходному напряжению, то есть исчезает при закорачивании выходных зажимов, то это обратная связь по напряжению (рис. 5.15).

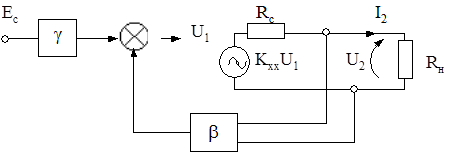Рис. 5.15. Расчетная схема усилителя с ООС по напряжению

По определению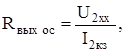

U_2xx=K_xxU_1xx=K_xx(gE_c-U_2xxb),

откуда после преобразования получим

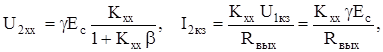
в результате имеем

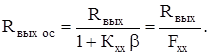(5.15)

Из (5.15) следует, что выходное сопротивление усилителя с ООС по напряжению меньше, чем у исходного усилителя в F_xx раз.

Это происходит за счет того, что при холостом ходе обратная связь достигает максимального, а выходное напряжение - минимального значения. В режиме же короткого замыкания обратная связь исчезает, что приводит к увеличению выходного тока.

Если напряжение обратной связи пропорционально выходному току, то есть исчезает при разрыве выходной цепи, то это обратная связь по току (рис. 5.16).

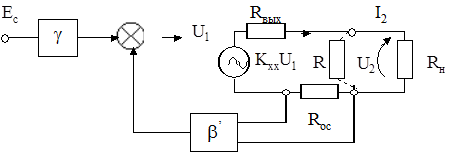Рис. 5.16. Расчетная схема усилителя с ООС по току

Здесь обязательным элементом цепи обратной связи является сопротивление R_ос, выполняющее роль преобразователя выходного тока в напряжение обратной связи. Цепь обратной связи с коэффициентом передачи b¢ отражает передачу напряжения, снимаемого с R_ос к управляющим зажимам

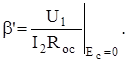
Определим выходное сопротивление при обратной связи по току

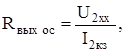
U_2xx=K_xxU_1xx=K_xxgE_c,

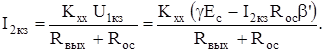
После преобразований получаем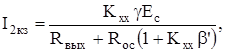

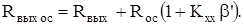(5.16)

Из (5.16) следует, что выходное сопротивление усилителя с ООС по току больше, чем у исходного усилителя.

Однако во многих случаях в усилителе имеется некоторая внутренняя нагрузка R, подключенная к выходным зажимам. При ее наличии отключение внешней нагрузки R_н не приводит к образованию чистого режима холостого хода. В результате выходное сопротивление становится равным

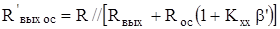
и в любом случае не может быть больше R.

Это обстоятельство обязательно необходимо учитывать при расчете параметров усилителя с ООС по току. Поскольку по определению

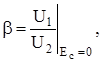
а введенное ранее значение 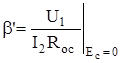выражено через выходной ток, то, с учетом очевидного равенства (см. рис. 5.16) 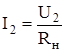, получаем 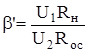откуда .

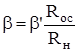Устойчивость усилителей с обратной связью

Подводя итог полученным в предыдущих разделах результатам, можно отметить, что в случае небольших фазовых сдвигов в петле отрицательная обратная связь обладает эффективным стабилизирующим и линеаризующим свойством, приводит к существенному уменьшению всех видов искажений, позволяет в необходимую сторону изменять значения входного и выходного сопротивления. Практически все полезные эффекты ООС оказываются пропорциональными глубине обратной связи F=1+Kb.

Поскольку в случае пассивной цепи обратной связи, которая в основном используется при построении стабильных усилительных устройств b£ 1, то увеличение глубины ООС возможно лишь за счет увеличения усиления исходного усилителя К, что достигается введением большого числа последовательно включенных усилительных каскадов.

Кроме значительного усложнения схемы, большое число каскадов приводит к увеличению фазового сдвига в петле обратной связи, что помимо снижения эффективности ООС может привести при определенных условиях к такому нежелательному явлению, как паразитная генерация.

Паразитная генерация - это появление на выходе усилителя сигнала, параметры которого не зависят от входного сигнала. То есть сигнал паразитной генерации может возникнуть и при отсутствии входного сигнала. Физически явление паразитной генерации возникает за счет передачи энергии с выхода усилителя через цепь обратной связи к его управляющим зажимам, то есть характерно именно для систем с обратной связью. Обычно напряжение паразитной генерации значительно больше уровня собственных шумов, что практически исключает нормальное функционирование усилительного устройства. При наличии паразитной генерации усилитель называется неустойчивым.

Обеспечение устойчивости является в большинстве случаев наиболее сложной проблемой, решаемой в процессе проектирования усилителей с глубокой ООС.

Поскольку паразитная генерация определяется внутренними процессами, происходящими в усилителе, то об устойчивости судят по виду решения линеаризованного дифференциального уравнения с нулевой правой частью (то есть при отсутствии внешнего возмущения) - характеристического уравнения, которое определяется знаменателем передаточной функции К_ос(р) или комплексного коэффициента передачи К_ос(jw). Для усилителя с ООС

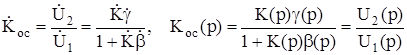
и характеристическое уравнение усилителя с ООС, таким образом, имеет вид

[1+K(p)·b (p)]=[1+T(p))]=0.

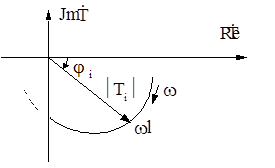Рис. 5.17. Годограф петлевого усиления

Решение такого уравнения ищется в виде

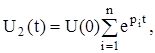
где U(0) - начальное условие, p_i - корни характеристического уравнения.

Корни могут быть чисто вещественными (р_i=± d_i) или комплексно сопряженными (р_i=±d _i ± jw ).

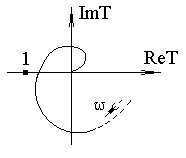Рис. 5.18. Годограф устойчивой системы

Очевидно, что если характеристическое уравнение имеет хотя бы один корень (простой или комплексно сопряженную пару) с положительной вещественной частью

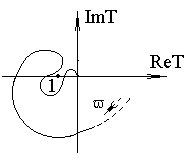Рис. 5.19. Годограф системы, устойчивой по Найквисту

d > 0,

то решение характеристического уравнения будет иметь одно слагаемое с нарастающим во времени коэффициентом

U(0)e^dit,

что и свидетельствует о неустойчивости усилителя. Таким образом, основным аналитическим признаком неустойчивости усилителя является наличие хотя бы одного корня характеристического уравнения с положительной вещественной частью.

Существуют различные признаки, позволяющие определить вид корней без решения характеристического уравнения. Такие признаки называются критериями устойчивости. Разработано большое число критериев.

Применительно к усилителям наибольшее распространение получил частотный критерий (критерий Найквиста), который позволяет судить об устойчивости по виду годографа АФЧХ петлевого усиления Т(jw).

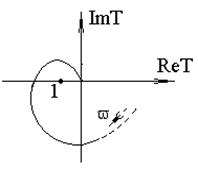Рис. 5.20. Годограф неустойчивой системы

Годограф - это геометрическое место точек, описываемое концом вектора Т в комплексной плоскости при изменении частоты от 0 до ¥. Каждой частоте внутри этого диапазона соответствует вектор, длина которого равна модулю, а угол поворота - фазе петлевого усиления (рис. 5.17).

Согласно частотному критерию, приводимому здесь без доказательств, усилитель будет устойчив, если годограф петлевого усиления T(jw) не охватывает точку с координатами -1, j0.

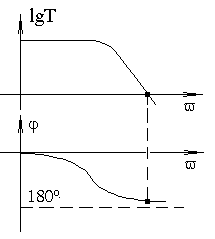Рис. 5.21. ЛАЧХ и ФЧХ устойчивой системы

На рис. 5.18, 5.19 показаны годографы устойчивых усилителей, а на рис. 5.20 - неустойчивого. Для практически наиболее часто применяемых усилителей с годографом, имеющим вид, изображенный на рис. 5.18 (с одним переходом фазы через 180^°), частотный критерий означает, что на частоте, где фаза петлевого усиления достигает 180^°, модуль петлевого усиления должен быть меньше единицы.

На рис. 5.21 и 5.22 приведены ЛАЧХ (АЧХ в логарифмическом масштабе) и ФЧХ соответственно для устойчивого и неустойчивого усилителей.

При рассмотрении ЛАЧХ нужно иметь в виду, что lg(Т=1)=0. Основным достоинством частотного критерия является возможность определения устойчивости по экспериментально снятым ЛАЧХ и ФЧХ для разомкнутой петли обратной связи.

Рис. 5.22. ЛАЧХ и ФЧХ неустойчивой системы

Современные усилители, особенно в микросхемном исполнении, обладают столь сложной структурой, что получить сколько-нибудь точное аналитическое описание ее практически не удается; именно в этих условиях частотный метод определения устойчивости приобретает важное значение.

Сигнал на выходе неустойчивого усилителя может принимать большие значения, при которых усилитель оказывается в нелинейном режиме, когда усилительные элементы выходного каскада оказываются неуправляемыми и через них может протекать настолько большой ток, что элемент выйдет из строя. Частотный же критерий позволяет определить устойчивость усилителя при разомкнутой петле обратной связи, когда система устойчива, что также подчеркивает его достоинство.

Коррекция частотных характеристик для обеспечения
устойчивости усилителя

Очевидно, что простой констатацией факта неустойчивости проектирование усилителя с ООС не может закончиться.

Устойчивость достигается коррекцией исходной частотной характеристики. Как будет показано далее, коррекция сопровождается значительным сужением исходной полосы рабочих частот. В специальной литературе определен оптимальный вид скорректированной ЛАЧХ, при которой достигается минимально возможное сужение исходной полосы частот. Однако для реализации оптимальной коррекции требуются сложные RLC-цепи с большим числом элементов. Поэтому на практике, особенно в случае усилителей в микросхемном исполнении, применяются простейшие корректирующие цепи RC-типа.

Простейшая коррекция достигается искусственным увеличением постоянной времени одного или двух каскадов путем, например, подключения к его выходным зажимам конденсатора определенной емкости. Увеличение постоянной времени приводит к уменьшению частоты среза и, как следствие, к более раннему спаду коэффициента усиления данного каскада и петлевого усиления в целом.

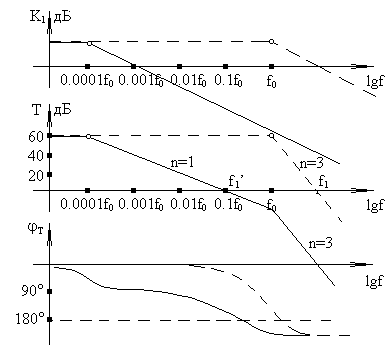Рис. 5.23. Исходные (пунктир) и скорректированные ЛАЧХ

Корректирующая емкость подбирается с таким расчетом, чтобы на частоте, где фаза достигает 180°, петлевое усиление успело снизиться до значения меньше единицы. На рис. 5.23 приведен пример такой коррекции.

Пунктиром изображены исходные ЛАЧХ одного каскада (К₁), петлевого усиления Т и ФЧХ петлевого усиления. Как видно, исходный усилитель является неустойчивым, поскольку на частоте f₁, где Т=1, фаза больше 180°.

Сплошными линиями изображены ЛАЧХ каскада К₁ после его коррекции, а также ЛАЧХ и ФЧХ петлевого усиления с учетом коррекции К₁. Усилитель стал устойчивым, поскольку на новой частоте единичного петлевого усиления f₁^’ фаза стала меньше 180°. Наклон ЛАЧХ в 6дБ/окт. обозначен на рис. 5.23 n=1, в 18 дБ/окт. - n=3.

Хорошо видно, что устойчивость путем простейшей коррекции достигнута за счет значительного сужения рабочей полосы частот.