Меры движения точки и механической системы

К мерам движения относят следующие характеристики их инертности и движения: количество движения (импульс) точки и системы, кинетический момент (момент количества движения) точки и системы относительно точки и оси, кинетическую энергию точки и системы.

2.3.1. Количество движения точки и механической системы

Количеством движением точки называют векторную величину, равную произведению массы точки на ее скорость

. (2.15)

Количеством движением механической системы называют сумму количеств движений всех ее точек

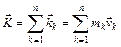. (2.16)

Эту величину можно выразить и через скорость центра масс (2.4)

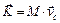. (2.17)

Размерность количества движения – кг·м/с.

2.3.2. Кинетический момент точки и механической системы

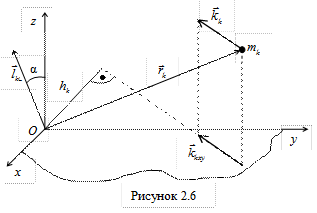
Кинетическим моментом или моментом количества движения материальной точки относительно некоторого центра О (рис. 2.6) называют векторную величину 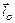, равную векторному произведению радиус-вектора точки , проведенного к ней из центра О, на вектор количества движения 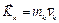этой точки

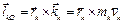. (2.18)

Модуль кинетического момента точки

. (2.19)

Кинетическим моментом материальной точки относительно оси называют проекцию на эту ось, например, Oz, кинетического момента относительно любой точки на этой же оси

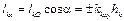. (2.20)

Значение кинетического момента положительное, если вращение перпендикуляра 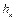вектором 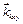наблюдается с положительного направления, например, оси Oz, против хода часовой стрелки; отрицательное – если наоборот. Значение, равное нулю, будет иметь место, когда вектор лежит в одной плоскости с соответствующей осью.

Кинетическим моментом механической системы относительно точки или оси называют сумму кинетических моментов всех точек системы относительно точки

(2.21)

или оси, например, оси Ох

. (2.22)

Кинетический момент тела вращения относительно его неподвижной оси,например, оси Oz, равен произведению момента инерции тела относительно этой оси на его угловую скорость

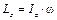. (2.23)

2.3.3. Кинетическая энергия точки и механической системы

Кинетической энергией материальной точки называют скалярную величину, равную половине произведения массы точки на квадрат ее скорости

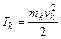. (2.24)

Кинетической энергией механической системы материальных точек называют сумму кинетических энергий всех точек этой системы

. (2.25)

Она равна нулю, если все точки системы в какой-то момент времени неподвижны.

Запишем выражения для кинетической энергии тела, совершающего

– поступательное движение

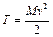, (2.26)

где М – масса тела, v – его скорость;

– вращательное движение

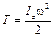, (2.27)

где 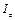– момент инерции тела относительно оси вращения, ω – его угловая скорость;

– плоскопараллельное движение

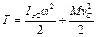, (2.28)

где 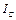– момент инерции тела относительно оси, проходящей через центр масс и перпендикулярной плоскости движения тела; ω – его угловая скорость; М – его масса; – скорость центра масс.

Размерность кинетической энергии – Джоуль, 1 Дж = 1 Н∙м.