Структура математической модели химического реактора. Математические модели высоких уровней иерархии включают в себя, как правило, несколько уравнений, как конечных

Математические модели высоких уровней иерархии включают в себя, как правило, несколько уравнений, как конечных, не содержащих операторов дифференцирования, так и дифференциальных, обыкновенных и в частных производных. Поэтому в общем случае математическая модель реактора – это достаточно сложная система уравнений, и количественные расчеты на основании этой модели целесообразно проводить, используя электронные вычислительные машины. Правильно разработанная модель химического реактора или химико-технологического процесса позволяет разработать и систему управления реактором или процессом в целом с использованием ЭВМ.

В то же время при описании химического процесса на нижних уровнях иерархической структуры часто возможно применение сравнительно простых математических методов. При этом достаточно отчетливо может просматриваться физическая сущность изучаемых явлений.

Протекающий в реакторе химический процесс представляет собой единство химической реакции и процессов переноса (тепло-, массопереноса и переноса импульса). Уравнения, входящие в математическую модель, должны учесть все эти явления. Однако, если для описания каждого из них использовать свои уравнения, математическая модель получится многомерной, что даже на низких уровнях иерархии затруднит нахождение решений такой системы уравнений, т. е. по сути дела осложнит технологический расчет реактора.

Поэтому при разработке математической модели стоит задача понизить размерность модели – по возможности объединить сущность отдельных элементов химического процесса в одном–двух уравнениях. Для уверенности в правильности выбора уравнений целесообразно в качестве исходных посылок использовать какие-либо фундаментальные законы, например законы сохранения. Поэтому правильно было бы составлять математическую модель химического процесса и химического реактора, отталкиваясь от законов сохранения массы и энергии.

Математическим выражением законов сохранения являются балансовые уравнения, прежде всего уравнения материального и энергетического балансов. В уравнении материального баланса можно учесть все изменения, которые происходят с веществом во времени и пространстве в результате химической реакции и диффузионных явлений (массопереноса) или при движении элементов потока в реакторе (при переносе импульса). Аналогично уравнение энергетического (теплового) баланса может учесть все энергетические изменения в реакторе, имеющие место как в ходе химической реакции, так и в результате процессов переноса.

Таким образом, сочетание только лишь двух уравнений – материального и теплового балансов может обеспечить получение достаточно полной математической модели химического процесса.

Так как химический процесс в реакторе протекает во времени и в пространстве, то для составления балансовых уравнений нужно предварительно выбрать некоторые элементарный объем ∆V и элементарный промежуток времени ∆τ.

Будем считать, что элементарным является такой объем, выделенный внутри реактора, в пределах которого можно пренебречь неравномерностью распределения концентраций и температуры. Элементарный объем неподвижен относительно аппарата и не передвигается вместе с реакционным потоком. В общем случае элементарный объем ∆V бесконечно мал во всех измерениях, но в некоторых частных случаях (например, для аппарата идеального смешения) его можно считать равным всему объему реактора.

Элементарным промежутком времени ∆τ является такой, в течение которого можно пренебречь изменениями концентрации и температуры внутри элементарного объема ∆V. Элементарный промежуток времени бесконечно мал для нестационарных режимов работы реактора и может быть выбран любым для стационарных режимов, например равным 1 ч или 1 мин.

Рассмотрим общую структуру балансовых уравнений.

Уравнения материального баланса (одно или несколько) составляют по тому или иному компоненту – участнику реакции (реагенту или продукту), отражая в уравнении все изменения, происходящие с этим компонентом. Если реакция сложная, математическое описание, как правило, включает в себя несколько уравнений материального баланса по нескольким веществам, каждое из которых участвует, по меньшей мере, в одной из простых реакций, составляющих сложную.

Уравнение материального баланса по веществу J учитывает все виды поступления, и расходования этого компонента в пределах элементарного объема ∆V течение промежутка времени ∆τ:

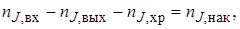
где n_J,вх– количество вещества J, внесенное в элементарный объем ∆V за время ∆τ с потоком участников реакции; п_J,вых – количество вещества J, вынесенное из объема ∆V за время ∆τ с потоком участников реакции;
n_J,хр – количество вещества J, израсходованное на химическую реакцию (или образовавшееся в результате ее протекания) в объеме ∆V за время ∆τ; n_J,нак – накопление вещества J в объеме ∆V за время ∆τ (изменение количества вещества J, одновременно содержащегося в объеме ∆V).

Аналогично составляют и уравнение теплового баланса. Для элементарного промежутка времени ∆τ рассматривают все тепловые потоки, которые входят, выходят или образуются внутри элементарного объема ∆V. Их алгебраическая сумма равна накоплению (изменению количества) теплоты в объеме ∆V за промежуток времени ∆τ:

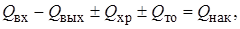
где Q_вx– теплосодержание веществ, входящих в объем ∆V завремя ∆τ; Q_вых – теплосодержание веществ, выходящих из объема ∆V за время ∆τ; Q_хр – теплота, выделившаяся или поглотившаяся в результате протекания химической реакции в объеме ∆V за время ∆τ; Q_то– теплота, израсходованная на теплообмен объема ∆V с окружающей средой за время ∆τ; Q_нак – накопление теплоты за время ∆τ в объеме ∆V.

При моделировании химических реакторов с использованием системного (иерархического) подхода можно идти двумя путями. Первый путь – от простого к сложному. Сначала целесообразно рассмотреть заведомо более простые (идеализированные) случаи протекания химических процессов в химических реакторах, а затем постепенно, снимая упрощающие ограничения, перейти к более общей модели.

Второй путь – обратный, от сложного – к более простому. Сначала, не вводя никаких упрощающих допущений, разработать математическую модель, пусть даже и сложную с точки зрения ее решения. Затем для определенных групп химических реакторов и режимов их работы ввести упрощающие допущения, справедливые только для этой группы реакторов, и получить более простые уравнения или системы уравнений, которые могут быть использованы в пределах действия принятых допущений.

Второй путь, по всей видимости, является, более общим. Используя его, выведем уравнение материального баланса, пригодное для описания любого реактора и любого режима его работы.