Определение физических и деформационных характеристик грунта.
По данным частных определений какой-либо характеристики физического состояния устанавливают ей нормативное значение Xn:
 , (3.71)
, (3.71)
где Xi - частное значение характеристики;
n - число определений характеристики (объём выборки).
Далее проверяют, не содержится ли среди частных определений Xi какие либо данные с грубым отклонением от общей совокупности результатов. Исключению из общей выборки подлежат максимальные и минимальные значения Xi, для которых выполняется условие
 , (3.72)
, (3.72)
где ν - статистический критерий, принимаемый по таблице 3.1.;
S - среднее квадратичное отклонение, вычисляемое по формуле:
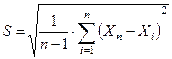 . (3.73)
. (3.73)
Таблица 3.1
Значения критерия n
| Число определений n | n | Число определений n | n | Число определений n | n |
| 2.07 | 2.80 | 3.03 | |||
| 2.18 | 2.82 | 3.04 | |||
| 2.27 | 2.84 | 3.05 | |||
| 2.35 | 2.86 | 3.06 | |||
| 2.41 | 2.88 | 3.07 | |||
| 2.47 | 2.90 | 3.08 | |||
| 2.52 | 2.91 | 3.09 | |||
| 2.56 | 2.93 | 3.10 | |||
| 2.60 | 2.94 | 3.11 | |||
| 2.64 | 2.96 | 3.12 | |||
| 2.67 | 2.97 | 3.13 | |||
| 2.70 | 2.98 | 3.14 | |||
| 2.73 | 3.00 | 3.14 | |||
| 2.75 | 3.01 | 3.15 | |||
| 2.78 | 3.02 | 3.16 |
Если отскоки имеются, то эти значения исключаются из выборки, вновь определяется среднее арифметическое и вновь делается проверка на наличие отскоков. После такой чистки должно быть 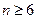 .
.
Принятое таким образом нормативное значение характеристики из-за естественной неоднородности грунта и ограниченного количества определений всегда на какую-то неопределённую величину отклоняется от истинного искомого значения (математического ожидания). Следовательно, нормативное значение содержит некоторую погрешность. Чтобы снизить её влияние, в расчётах используются не нормативные, а расчётные характеристики свойств грунтов.
Расчётная характеристика Х определяется по формуле
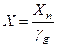 , (3.74)
, (3.74)
где γg - коэффициент надёжности по грунту.
Для всех физических характеристик, кроме плотности и удельного веса грунта, СНиП 2.02.01-83* допускает принимать 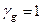 . Расчётное значение плотности и удельного веса грунта находят с учётом показателя точности оценки её среднего значения аналогично прочностным и деформационным характеристикам грунта.
. Расчётное значение плотности и удельного веса грунта находят с учётом показателя точности оценки её среднего значения аналогично прочностным и деформационным характеристикам грунта.
Деформационные характеристики грунтов вычисляются по формулам (3.71) и (3.74). При этом определение модуля деформации грунта в лабораторных условиях должно проводиться не менее чем по шести образцам. В полевых условиях при испытаниях штампом ограничиваются тремя опытами (или даже двумя, если их результаты отличаются от среднего не более чем на 25%).
3.6.2. Определение нормативных и расчётных значений прочностных характеристик грунта.
Обработка результатов испытаний грунтов на срез с целью определения нормативных значений сцепления сn и угла внутреннего трения jn производится путём вычисления методом наименьших квадратов прямолинейной зависимости (рис.3.10, 3.13) для всей совокупности опытных величин t в инженерно-геологическом элементе:
Нормативные значения сn и tg jn вычисляются по формулам:
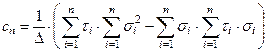 , (3.75)
, (3.75)
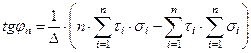 , (3.76)
, (3.76)
где n - число экспериментов по определению предельного сопротивления сдвигу τi при данных σi;
Δ - общий знаменатель этих выражений:
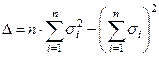 . (3.77)
. (3.77)
Расчётные значения прочностных характеристик с, φ и Rc (где Rc – временное сопротивление на сжатие образцов скальной породы в водонасыщенном состоянии), плотности и удельного веса грунта определяют по формуле (3.74), где коэффициент надёжности по грунту вычисляют из выражения
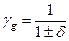 , (3.78)
, (3.78)
где δ - доверительный интервал, характеризующий область вокруг среднего значения, в пределах которого с заданной вероятностью α находится “истинное” (генеральное) среднее значение. Знак перед показателем δ выбирают так, чтобы обеспечить большую надёжность расчёта.
Показатель точности оценки среднего значения характеристики грунта δ вычисляется по формулам:
для с и tg j 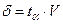 (3.79)
(3.79)
для Rc и g 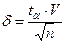 (3.80)
(3.80)
где ta - коэффициент Стьюдента, принимаемый по табл. 3.2 в зависимости от заданной доверительной вероятности a и числа определений n:
Значения коэффициентов Стьюдента ta таблица 3.2
| Число определений (n-1) для Rc и g | Коэффициент ta при односторонней доверительной вероятности a, равной | ||||
| (n-2) для с и j | 0.85 | 0.90 | .0.95 | 0.98 | 0.99 |
| 1.34 | 1.89 | 2.92 | 4.87 | 6.96 | |
| 1.25 | 1.64 | 2.35 | 3.45 | 4.54 | |
| 1.19 | 1.53 | 2.13 | 3.02 | 3.75 | |
| 1.16 | 1.48 | 2.01 | 2.74 | 3.36 | |
| 1.13 | 1.44 | 1.94 | 2.63 | 3.14 | |
| 1.12 | 1.41 | 1.90 | 2.54 | 3.00 | |
| 1.11 | 1.40 | 1.86 | 2.49 | 2.90 | |
| 1.10 | 1.38 | 1.83 | 2.44 | 2.82 | |
| 1.10 | 1.37 | 1.81 | 2.40 | 2.76 | |
| 1.09 | 1.36 | 1.80 | 2.36 | 2.72 | |
| 1.08 | 1.36 | 1.78 | 2.33 | 2.68 | |
| 1.08 | 1.35 | 1.77 | 2.30 | 2.65 | |
| 1.08 | 1.34 | 1.76 | 2.28 | 2.62 | |
| 1.07 | 1.34 | 1.75 | 2.27 | 2.60 | |
| 1.07 | 1.34 | 1.75 | 2.26 | 2.58 | |
| 1.07 | 1.33 | 1.74 | 2.25 | 2.57 | |
| 1.07 | 1.33 | 1.73 | 2.24 | 2.55 | |
| 1.07 | 1.33 | 1.73 | 2.23 | 2.54 | |
| 1.06 | 1.32 | 1.72 | 2.22 | 2.53 | |
| 1.06 | 1.32 | 1.71 | 2.19 | 2.49 | |
| 1.05 | 1.31 | 1.70 | 2.17 | 2.46 | |
| 1.05 | 1.30 | 1.68 | 2.14 | 2.42 | |
| 1.05 | 1.30 | 1.67 | 2.12 | 2.39 |
V - коэффициент вариации характеристики, вычисляемый по формуле:
 (3.81)
(3.81)
где Xn - нормативное значение характеристики;
S - среднее квадратичное отклонение характеристики, вычисляемое:
1. для с и tg j по формулам:
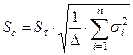 , (3.82)
, (3.82)
 , (3.83)
, (3.83)
где 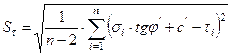 (3.84)
(3.84)
Δ - определяется по формуле (3.77).
2. для Rc и γ: 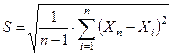 (3.85)
(3.85)
При расчётах по первой группе предельных состояний (по несущей способности) расчётные характеристики определяют при доверительной вероятности 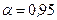 и часто обозначают как tgφI, cI, γI, При расчётах по второй группе предельных состояний (по деформациям) – при
и часто обозначают как tgφI, cI, γI, При расчётах по второй группе предельных состояний (по деформациям) – при 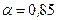 и обозначают tgφII, cII, γII.
и обозначают tgφII, cII, γII.
Дата добавления: 2015-06-17; просмотров: 825;
