Классификация вирусов. Определение 2.31. Для всех геделевских нумераций частичных рекурсивных функций , для всех вирусов v по отношению к :

Определение 2.31. Для всех геделевских нумераций частичных рекурсивных функций 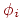, для всех вирусов v по отношению к :

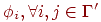· i вредоносна по отношению к v и j

• i = v(j)
• 

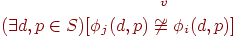
Существует состояние системы, при котором зараженная вирусом v программа j выполняет вредоносную функцию, т.е. результат действия зараженной программы не ограничивается заражением (появлением новых зараженных программ).

• i заразна по отношению к v и j
• i = v(j)
• 

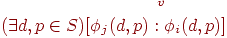
Существует состояние системы, при котором зараженная вирусом v программа j выполняет функцию размножения - в результате ее действия в системе появляются новые зараженные программы.

• i безобидна по отношению к v и j
• i = v(j)
• i не вредоносна по отношению к j
• i не заразна по отношению к j
• i является трояном по отношению к v и j
• i = v(j)
• вредоносна по отношению к j
• i не заразна по отношению к j

Троян способен только к выполнению вредоносных функций и не может размножаться.

• i является переносчиком по отношению к v и j
• i = v(j)
• не вредоносна по отношению к j
• i заразна по отношению к j

Переносчик является антиподом трояна: он только размножается и не содержит вредоносных функций.

• i является вирусом по отношению к v и j
• i = v(j)
• i вредоносна по отношению к j
• i заразна по отношению к j

Вирус - наиболее универсальный тип вредоносных программ, способный как к размножению, так и к выполнению вредоносных действий.

В тех случаях когда существует единственная j такая, что (т.е. когда v инъективна) и i является вредоносной (заразной, безобидной, трояном, переносчиком, вирусом) по отношению к v и j, ссылка на j будет опускаться и i будет называться вредоносной (заразной, безобидной, трояном, переносчиком, вирусом) по отношению к v.

Таким образом, если по отношению к какому-либо вирусу инфицированная программа является безобидной, это значит что она выполняет в точности те же действия, что и исходная неинфицированная программа и никаких других. Если она является трояном, значит она не может заражать другие программы, а может только имитировать их действия или наносить вред. Если программа является переносчиком, значит она не способна наносить вред, но при определенных обстоятельствах может заражать другие программы.

Определение 2.32. Для всех геделевских нумераций частичных рекурсивных функций 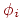, для всех вирусов v по отношению к :

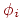• вирус v безобиден одновременно справедливо:
• ( j Γ') [v(j) не является вредоносной по отношению к v и j]
• ( j Γ') [v(j) не является заразной по отношению к v и j]
• вирус v - троянский конь одновременно справедливо:
• ( j Γ') [v(j) является вредоносной по отношению к v и j]
• ( j Γ') [v(j) не является заразной по отношению к v и j]
• вирус v только распространяется одновременно справедливо:
• ( j Γ') [v(j) не является вредоносной по отношению к v и j]
• ( j Γ') [v(j) является заразной по отношению к v и j]
• вирус v вредоносен одновременно справедливо:
• ( j Γ') [v(j) является вредоносной по отношению к v и j]
• ( j Γ') [v(j) является заразной по отношению к v и j]

Следующая теорема отмечает ряд простых свойств, присущих различным типам вирусов.

Теорема 2.11. Для всех геделевских нумераций частичных рекурсивных функций 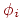, для всех вирусов v по отношению к :

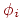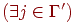1. [v(j) безобидна по отношению к v и j]
2. вирус v безобиден 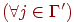[v(j) безобидна по отношению к v и j]
3. если v - троян, то 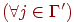[v(j) безобидна по отношению к v и j] или [v(j) является трояном по отношению к v и j]
4. если v способен только распространяться, то 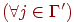[v(j) безобидна по отношению к v и j] или [v(j) является переносчиком по отношению к v и j]

Доказательство. Первое свойство непосредственно следует из первой теоремы о рекурсии (теоремы о неподвижной точке).

Остальные свойства следует непосредственно из определений.