Оценка сложности сигнатурного метода

Далее в своей работе Ф. Лейтольд обращается к проблеме обнаружения не всех возможных вирусов, а некоторого подмножества "известных" вирусов.

Для этого предлагается сигнатурный метод - обнаружение вируса по строке или подстроке его кода. Естественно, таким образом невозможно обнаружить полиморфные вирусы. Но для обнаружения обычных или олигоморфных вирусов такой способ годится: олигоморфные вирусы могут обнаруживаться по строке или подстроке кода расшифровщика.

В случаях, когда обнаружение осуществляется по подстроке вирусного кода (либо даже по полному коду распаковщика для олигоморфных вирусов) возможны ложные срабатывания. Ф. Лейтольд приводит оценку вероятности ложных обнаружений при следующих допущениях:

• Длина сигнатуры - N
• Общая длина анализируемых данных - L >> N
• Количество символов в алфавите - n, и встречаются они в анализируемых данных с равной вероятностью
• Количество известных вирусов M

В этом случае оценка количества ложных обнаружений будет примерно равна:

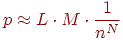
Можно также подсчитать вычислительную сложность алгоритма, выполняющего поиск вирусов по сигнатуре. Для выполнения поиска требуется последовательно сравнить все ячейки анализируемой строки данных с первыми ячейками сигнатур. В общем случае это L·M сравнений. Далее, при обнаружении совпадения потребуется провести сравнение со второй ячейкой сигнатуры. Учитывая вероятность совпадения значения первой ячейки, количество сравнений второй ячейки будет 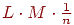. Аналогично, третьей - 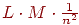и т. д. Общее количество сравнений составит:

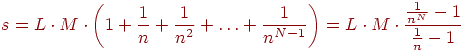
В худшем сценарии, когда все сигнатуры полностью различны, а n и N достаточно велики, количество сравнений составит s = L·M·N.

Следовательно, сигнатурный поиск может быть выполнен за полиномиальное время.

Необходимо понимать, что полученные оценки приблизительны и соответствуют худшему варианту поиска случайной подпоследовательности в случайной последовательности. На практике код программы и код вируса не являются случайными последовательностями и с учетом знания их структуры алгоритм поиска может быть существенно оптимизирован, оценка времени - уменьшена.