Электронно - дырочный переход при постоянном смещении.
Выше было рассмотрено состояние термодинамического равновесия р-п перехода, при котором суммарный ток через него был равен нулю. Состояние термодинамического равновесия может быть нарушено, если к р-п переходу приложить внешнее напряжение.
p-п переход при обратном смещении. Рассмотрим случай, когда к р области кристалла подключен отрицательный полюс внешней батареи, а к n области - положительный (рис.1.6).
 Такое включение называют обратным, считают U<0, и говорят: р-п переход смещен в обратном направлении. При таком смещении перехода дырки и электроны будут оттягиваться от границы раздела, что приведет к расширению области объемного заряда. Все приложенное напряжение практически будет падать на р-п переходе, поскольку эта область кристалла обладает высоким сопротивлением. Поэтому высота потенциального барьера при обратном смещении перехода увеличится и будет равна jк = jк0+ U.
Такое включение называют обратным, считают U<0, и говорят: р-п переход смещен в обратном направлении. При таком смещении перехода дырки и электроны будут оттягиваться от границы раздела, что приведет к расширению области объемного заряда. Все приложенное напряжение практически будет падать на р-п переходе, поскольку эта область кристалла обладает высоким сопротивлением. Поэтому высота потенциального барьера при обратном смещении перехода увеличится и будет равна jк = jк0+ U.
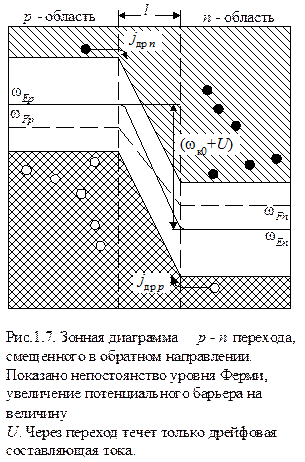 На рис. 1.7 показана зонная диаграмма р-п перехода при обратном смещении. Уровень Ферми на диаграмме уже не изображается горизонтальной прямой: для n области он смещается вниз по отношению к уровню Ферми р области на величину U.
На рис. 1.7 показана зонная диаграмма р-п перехода при обратном смещении. Уровень Ферми на диаграмме уже не изображается горизонтальной прямой: для n области он смещается вниз по отношению к уровню Ферми р области на величину U.
|
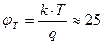 мВ при комнатной температуре), то диффузионная составляющая тока составит приблизительно 2% от своего равновесного значения. При U = 0.5 В потенциальный барьер уже практически непреодолим для основных носителей, и диффузионный ток через переход становится равным нулю.
мВ при комнатной температуре), то диффузионная составляющая тока составит приблизительно 2% от своего равновесного значения. При U = 0.5 В потенциальный барьер уже практически непреодолим для основных носителей, и диффузионный ток через переход становится равным нулю.
Увеличение потенциального барьера не меняет дрейфовую составляющую тока, так как ее величина определяется количеством неосновных носителей, появляющихся на границе области объемного заряда в каждую единицу времени. Это количество для данного полупроводника при данной температуре является постоянным. Поле в переходе будет лишь определять скорость переброса неосновных носителей из одной области в другую, но не число носителей, переходящих его в единицу времени.
Таким образом, в рассматриваемом случае Iдиф - Iдр ¹ 0, так как Iдиф < Iдр, и через переход потечет ток, называемый обратным током Iобр (рис. 1.6 ). При возрастании обратного напряжения приблизительно до 0.1 В обратный ток Iобр = Iдиф - Iдр будет увеличиваться за счет уменьшения диффузионной составляющей. При напряжениях больших 0.1 В можно считать Iдиф = 0, и через переход будет идти только дрейфовая компонента тока, которая не зависит от приложенного напряжения. По этой причине ее часто называют током насыщения перехода и обозначают через Iо. Величина тока Iобудет мала, поскольку она является током неосновных носителей, концентрация которых незначительна.
 p-n переход при прямом смещении. Поменяем полярность батареи и включим ее так, как показано на рис. 1.8. Такое включение называют прямым, считают что U > 0 и в данном случае p-n переход смещен в прямом направлении. В этом случае основные носители-электроны и дырки будут двигаться к границе раздела (рис. 1.8) и частично компенсировать заряд ионизированных атомов акцепторов и доноров. Область объемного заряда уменьшится. По-прежнему почти все внешнее напряжение будет падать на p-n переходе, и высота потенциального барьера будет
p-n переход при прямом смещении. Поменяем полярность батареи и включим ее так, как показано на рис. 1.8. Такое включение называют прямым, считают что U > 0 и в данном случае p-n переход смещен в прямом направлении. В этом случае основные носители-электроны и дырки будут двигаться к границе раздела (рис. 1.8) и частично компенсировать заряд ионизированных атомов акцепторов и доноров. Область объемного заряда уменьшится. По-прежнему почти все внешнее напряжение будет падать на p-n переходе, и высота потенциального барьера будет 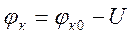 .
.
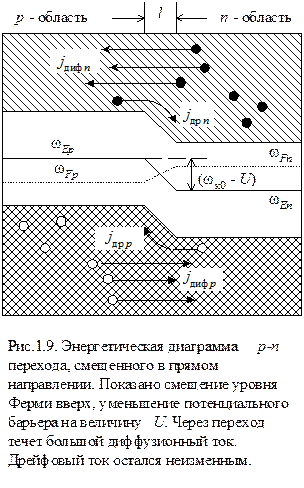 На рис. 1.9 представлена зонная диаграмма p-n перехода, смещенного в прямом направлении. Как и в первом случае, происходит относительное вертикальное смещение уровней Ферми но в противоположном направлении (сравни с рис. 1.7). Из рис. 1.9 видно, что с уменьшением высоты потенциального барьера возрастает число основных носителей по обе стороны от перехода, обладающих достаточной энергией, чтобы преодолеть барьер.
На рис. 1.9 представлена зонная диаграмма p-n перехода, смещенного в прямом направлении. Как и в первом случае, происходит относительное вертикальное смещение уровней Ферми но в противоположном направлении (сравни с рис. 1.7). Из рис. 1.9 видно, что с уменьшением высоты потенциального барьера возрастает число основных носителей по обе стороны от перехода, обладающих достаточной энергией, чтобы преодолеть барьер.
Диффузионная составляющая тока через переход, увеличится по сравнению с равновесным значением. Дрейфовая компонента тока остается неизменной. Поэтому Iдиф - Iдр ¹ 0, так как Iдиф > Iдр. Через переход потечет прямой Iпр (рис.1.9 ) равный разности диффузионного и дрейфового токов. C увеличением прямого напряжения диффузионный и, следовательно, прямой ток будет возрастать и достигать весьма больших значений.
При изменении полярности напряжения на p-n переходе отношение прямого тока к обратному может составлять сотни тысяч и миллионы раз. Это позволяет говорить о направлении пропускания (прямое напряжение на переходе) и
направлении запирания (обратное напряжение).
Ширина p-n перехода при постоянном смещении. Как уже отмечалось, ширина p-n переход изменяется при подключении к нему внешнего напряжения.
Ширину p-n перехода в неравновесном состоянии можно определить, подставив в выражение (1.7 ) вместо jк0 значение jк = jк0 - U. Тогда получим
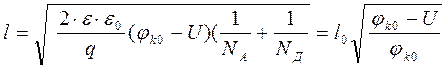 (1.9)
(1.9)
Отсюда видно, что переход сужается при прямом смещении ( U > 0 ) и расширяется при обратном смещении ( U < 0 ).
Граничные концентрации неравновесных неосновных носителей. Включение внешней батареи приводит к важному следствию - изменению концентраций неосновных носителей по обе стороны от p-n перехода.
Под граничной концентрацией носителей понимают их концентрацию на границе собственно p-n перехода с основной p или n областью. Определить зависимость граничных концентраций неосновных носителей от приложенного к p-n переходу постоянного напряжения можно, используя выражения (1.3 ). Из них следует:
 (1.10 )
(1.10 )
где 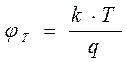 - температурный потенциал полупроводника. Индекс "0" в этих формулах используется для обозначения равновесного значения концентраций.
- температурный потенциал полупроводника. Индекс "0" в этих формулах используется для обозначения равновесного значения концентраций.
В неравновесном состоянии концентрации неосновных носителей pn и np определяются из (1.10 ), если заменить jк0 на jк = jк0 – U :
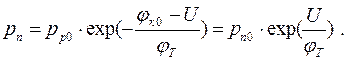 (1.11 а )
(1.11 а )
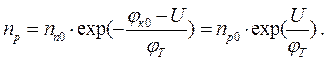 (1.11 б )
(1.11 б )
Выражения (1.11) показывают, что при прямом смещении (U > 0) происходит увеличение концентраций неосновных носителей на границах перехода по сравнению с равновесными значениями. Иначе говоря, в каждой из областей р-п кристалла появляются избыточные, или неравновесные неосновные носители. Процесс введения избыточных носителей получил название инжекции.
При обратном смещении (U < 0) происходит уменьшение граничных концентраций, т.е. pn < pno и np < npo. Такой процесс "отсоса" неосновных носителей называют экстракцией.
Вычитая из pn pno и из np npo, получим величины избыточных граничных концентраций:
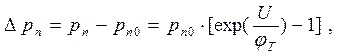 (1.12 а)
(1.12 а)
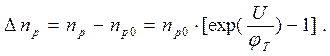 (1.12 б)
(1.12 б)
Поделим (1.12 а) на (1.12 б) и учтем (1.1 ),тогда
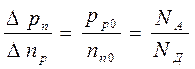 . (1.13 )
. (1.13 )
В симметричных переходах ( NА » NД ) D np » D pn , т.е. инжекция носит
двусторонний характер. В несимметричных — односторонний. Например, при NА >> NД , Dpn >> Dnp , т.е. носители инжектируются из низкоомного полупроводника в высокоомный. В этом случае низкоомную инжектирующую область называют эмиттером, а высокоомную - базой p-n кристалла.
Вольтамперная характеристика перехода. При выводе уравнения вольтамперной характеристики перехода принимаются следующие упрощающие анализ допущения.
1. Переход считается плоскопараллельным, благодаря чему задача становится одномерной.
2. Ширина перехода мала, что позволяет пренебречь процессами генерации и рекомбинации носителей в переходе.
3. Приложенное напряжение падает на области p-n перехода, т.е. электрическое поле вне области перехода отсутствует, следовательно, токи определяются только процессами диффузии.
4. Отсутствуют поверхностные утечки.
5. Распределение примесей однородно.
6. Ширина n и р областей бесконечна.
Для определения токов через электронно-дырочный переход следует решить уравнения непрерывности совместно с уравнениями для плотности токов. В одномерном случае эти уравнения имеют вид:
для дырок n области
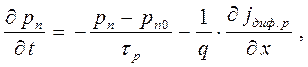 (1.14 а)
(1.14 а)
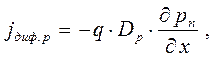 (1.14 б)
(1.14 б)
для электронов p области
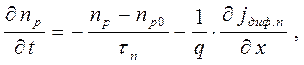 (1.15 а)
(1.15 а)
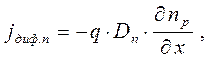 (1.15 б)
(1.15 б)
В этих уравнениях D p,n - коэффициент диффузии, a t p,n - время жизни дырок и электронов соответственно, x - расстояние, отсчитываемое от границы перехода в глубь дырочной или электронной области. Уравнения (1.14 а) и (1.15 а) получили названия уравнений диффузии. Так как мы хотим получить зависимость постоянного тока через р-п переход от приложенного постоянного
напряжения то в уравнения диффузии следует положить 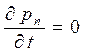 ,
, 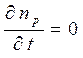 ,
,
Найдем вначале дырочную составляющую тока. Для этого подставим в
(1.14 а) (1.14 б), и, учитывая, что 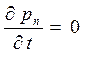 , получим:
, получим:
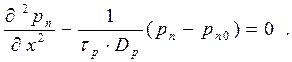 (1.16)
(1.16)
Решение уравнения (1.16 ) запишем в виде:
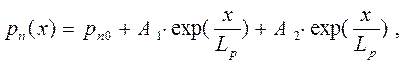
где 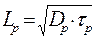 - диффузионная длина дырок, физический смысл которой будет выяснен ниже. Постоянные A1 и A2 определяются из граничных условии:
- диффузионная длина дырок, физический смысл которой будет выяснен ниже. Постоянные A1 и A2 определяются из граничных условии:
при x=0 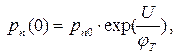 , при x → ∞
, при x → ∞ 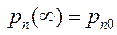 .
.
Тогда окончательное решение принимает вид:
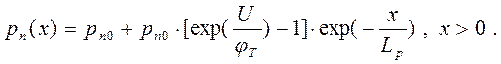 (1.17 )
(1.17 )
Аналогичным образом решается диффузионное уравнение (1.15 а):
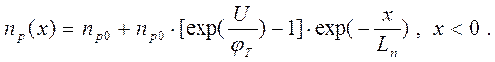 (1.18 )
(1.18 )
где Ln - диффузионная длина электронов, а отрицательная координата х отсчитывается от границы перехода в глубь n области (рис. 1.10 ) концентрации неравновесных неосновных носителей с ростом x уменьшаются за счет рекомбинации с основными носителями и стремятся к равновесным значениям.
На рис.1.10 показано распределение концентрации неравновесных неосновных носителей при прямом смещении р-n перехода.
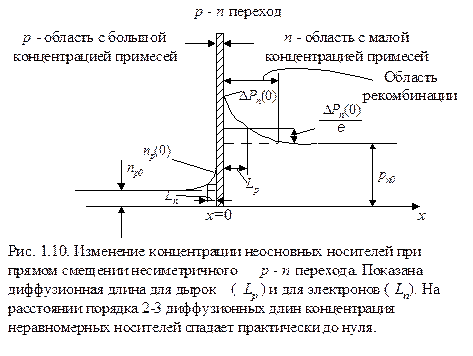 Теперь можно уточнить: диффузионная длина - это такое расстояние, на котором неравновесная концентрация неосновных носителей уменьшается в е раз по сравнению с ее граничным значением, т.е. Dp(0) или Dn(0).
Теперь можно уточнить: диффузионная длина - это такое расстояние, на котором неравновесная концентрация неосновных носителей уменьшается в е раз по сравнению с ее граничным значением, т.е. Dp(0) или Dn(0).
Неравновесное распределение дырок (1.17) и электронов (1.18) обусловливает диффузионные токи Iдиф p и Iдиф n , плотности которых могут быть найдены подстановкой (1.17 ) и (1.18 ) в (1.14 б) и (1.15 б) соответственно. В результате получается:
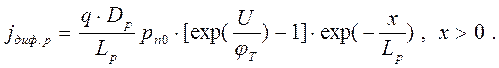 (1.19)
(1.19)
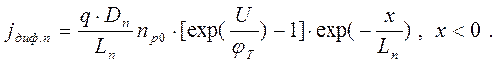 (1.20)
(1.20)
Хотя jдиф p и jдиф n зависят от х, общий ток постоянен в любом cечении р-n полупроводника. Вблизи границ р-n перехода (x » 0) этот ток будет практически диффузионным, и поэтому он может быть найден как сумма jдиф p и jдиф n при х = 0 т. е.
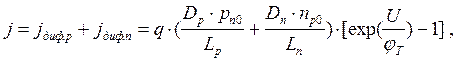
Соответственно ток через р-n переход площадью S равен
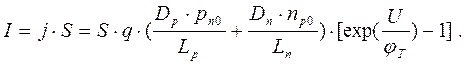
Эту формулу запишем в виде 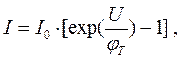 (1.21)
(1.21)
где 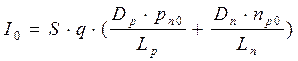 (1.22)
(1.22)
Формула (1.21 ) описывает статическую вольтамперную характеристику p-n перехода, график которой показан на рис. 1.11.
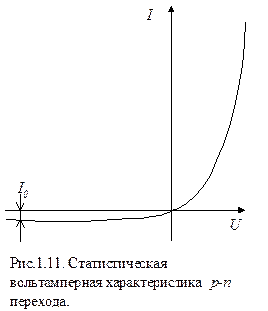 Особенностью характеристики является очень крутая (экспоненциальная) прямая ветвь и пологая обратная, т.е. электронно-дырочный переход обладает резко выраженной односторонней проводимостью. В связи с большой крутизной прямой ветви удобнее задавать в качестве независимой переменный ток, а напряжение считать его функцией:
Особенностью характеристики является очень крутая (экспоненциальная) прямая ветвь и пологая обратная, т.е. электронно-дырочный переход обладает резко выраженной односторонней проводимостью. В связи с большой крутизной прямой ветви удобнее задавать в качестве независимой переменный ток, а напряжение считать его функцией: 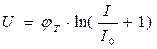 . (1.23 )
. (1.23 )
Выражение (1.23 ) получается путем логарифмирования (1.21 ).
Рассмотрим выражение для тока I0, входящего "масштабным" множителем в уравнение вольтамперной характеристики. С учетом (1.1 ) и того, что 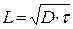 , оно принимает вид:
, оно принимает вид:
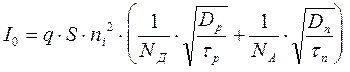 .
.
Поскольку 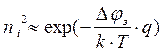 , где Djз - ширина запрещенной зоны,
, где Djз - ширина запрещенной зоны,
то, во-первых, ток насыщения I0 перехода будет увеличиваться по экспоненте с ростом температуры. По этой причине его часто называют тепловым. Во-вторых, ток I0 будет тем меньше, чем больше Djз . Так, у кремния Djз = 1.12 В, а у германия Djз = 0.66 В. Поэтому ток I0 кремниевого p-n перехода оказывается на несколько порядков меньше германиевого.
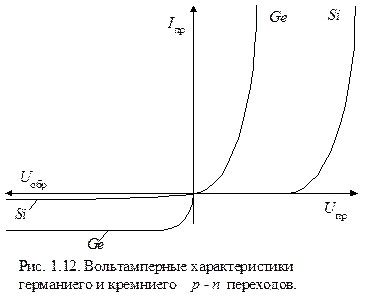 На (рис. 1.12) дано качественное сравнение вольтамперных характеристик германиевого и кремниевого р-n переходов. Видно, что прямая ветвь вольтамперной характеристики кремниевого перехода как бы сдвинута вправо по оси напряжений (на 0.3-0.4В) относительно характеристики германиевого p-n перехода. Этот сдвиг обусловлен отмеченным выше различием токов насыщения. По этой же причине различен и ход обратных ветвей.
На (рис. 1.12) дано качественное сравнение вольтамперных характеристик германиевого и кремниевого р-n переходов. Видно, что прямая ветвь вольтамперной характеристики кремниевого перехода как бы сдвинута вправо по оси напряжений (на 0.3-0.4В) относительно характеристики германиевого p-n перехода. Этот сдвиг обусловлен отмеченным выше различием токов насыщения. По этой же причине различен и ход обратных ветвей.
Прохождение тока через p-n переход . Основываясь на полученных выше результатах, поясним механизм протекания тока через переход.
Механизм протекания обратного тока через переход относительно прост. В результате действия обратного напряжения граничные концентрации неосновных носителей уменьшается по сравнению с равновесными значениями. Возникает градиент концентрации неосновных носителей, за счет которого они будут диффундировать в сторону области объемного заряда. Достигнув области объемного заряда, носители подхватываются полем и переносятся через переход в область, где они становятся уже основными носителями. Так как pn << pp и np << nn , то появление в той или иной области полупроводника небольшого дополнительного количества основных носителей заряда практически не изменяет его равновесного состояния.
Более сложная картина получается при протекании прямого тока. При положительном внешнем напряжении на р-п переходе будет иметь место инжекция дырок и электронов соответственно в р и п область. Для простоты будем рассматривать процессы в области п полупроводника так как в области р процессы будут протекать аналогичным образом.
Дырки, инжектированные в п область создают градиент концентрации неосновных носителей в следствии чего возникает диффузионный поток дырок. Инжекция дырок вначале нарушает электрическую нейтральность п области. Для ее восстановления от внешнего источника в п область входят электроны в количестве, равном количеству инжектированных дырок, т.е. в п области появляются неравновесные основные носители. Процесс компенсации протекает очень быстро, приблизительно за с. Электроны, поступающие из внешней цепи, двигаются в сторону электронно-дырочного перехода и рекомбинируют там с дырками, поддерживая тем самым их стационарное распределение. На место прорекомбинировавших электронов приходят все новые и новые и, таким образом, создается ток основных носителей-электронов, двигающихся справа налево. По мере приближения к переходу этот ток будет уменьшаться до нуля за счет рекомбинации электронов с дырками (область рекомбинации показана на рис. l.10), и вблизи p-n перехода будет идти лишь диффузионный ток дырок слева направо.
На расстоянии, большем (3-4)Lp от перехода, диффузионный ток становится равным нулю, и весь ток здесь создается током основных носителей. Суммарный же ток остается постоянным в любом сечении.
Характеристические сопротивления перехода . Электрические свойства
р-n перехода характеризуются дифференциальным сопротивлением 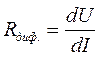 . Дифференцируя (1.23.), получим
. Дифференцируя (1.23.), получим
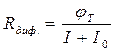 (1.24)
(1.24)
При комнатной температуре jт » 25 мВ. Поэтому часто пользуются форму-
лой 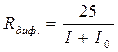 , где ток выражен в миллиамперах, а Rдиф. - в омах.
, где ток выражен в миллиамперах, а Rдиф. - в омах.
При работе р-п перехода на постоянном токе его свойства характеризуют
сопротивлением постоянному току 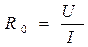 . С учетом (1.21) и (1.23 )
. С учетом (1.21) и (1.23 )
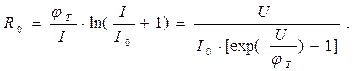 (1.25)
(1.25)
В силу нелинейности вольтамперной характеристики р-п перехода R диф. и
R 0 различны: в области прямых токов R 0 всегда больше Rдиф. , а в области обратных - R 0 всегда меньше R диф. .
Дата добавления: 2015-06-12; просмотров: 2613;
