Электронно-дырочный переход в условиях равновесия.

Понятие p-n перехода. Электронно-дырочным переходом называется переходный слой, разделяющий электронную и дырочную области полупроводника, обеднённый носителями заряда. Электронно-дырочный, или просто р-n переход является основным элементом многих полупроводниковых приборов, в том числе и полупроводниковых диодов.

Образование p-n перехода. Токи через переход. Предположим, что имеются полупроводники типа р и типа n. 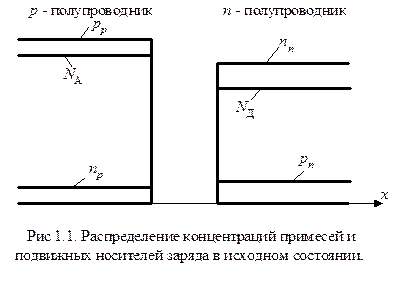На рис. 1.1. схематически показано распределение концентраций акцепторов N_А, доноров N_Д и подвижных носителей заряда р и n в этих полупроводниках. Для простоты представим, что р и n полупроводники приведены в соприкосновение так, чтобы образовалась плоская граница раздела без нарушения струк­туры кристаллической решетки (на практике получение таких идеальных контактов осуществляется специальным технологическим путем). Что же произойдет в этом случае на полученном путем соприкосновения полупроводиков р-n переходе?

Так как концентрации одноименных подвижных носителей заряда (электронов и дырок) по обе стороны от границы раздела существенно отличаются, в таком контакте будет наблюдаться диффузионный ток электронов из n в p область и диффузионный ток дырок из р в n область. Ушедшие из n области электроны оставляют после себя положительно ионизированные атомы доноров, а атомы акцепторов, захватившие перешедшие электроны, становятся ионизированными отрицательно. Вбли­зи границы раздела электронного и дырочного полупроводников возникают области неподвижных положительного (в n полупроводнике) и отрица­тельного (в р ­- полупроводнике) объемных не скомпенсированных заря­дов, и обе области заряжаются одна относительно другой. За предела­ми области объемного заряда полупроводник остается электрически нейтральным. Электрически нейтральным, конечно, будет и p-n полупроводник в целом. Поэтому объемные заряды слева и справа от границы раздела должны быть одинаковыми. 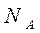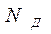При этом, если концентрации примесей и не равны, то и протяженность объемных зарядов будет различной.

Так, при 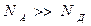область положительного заряда будет гораздо шире, чем область отрицательного заряда. Область образовавшихся объемных зарядов и есть собственно область p-n перехода. Ее протяженность обычно составляет десятые доли микрона.

Нескомпенсированные объемные заряды приводят к возникновению на границе раздела контактной разности потенциалов и электрического по­ля, направление которого препятствует дальнейшей диффузии зарядов. Однако, некоторые электроны и дырки, обладающие достаточновысокой энергией, оказываются все же в состоянии преодолеть действие сил электрического поля, и через границу раздела будут продолжать идти диффузионные токи.

Поскольку ток в разомкнутой цепи равен нулю, то диффузионные токи должны быть уравновешены. Уравновешивающими токами являются два встречных потока неосновных носителей (дрейфовые токи), переходящие границу раздела под действием электрического поля перехода.

Таким образом, в равновесном состоянии через границу раздела будут протекать четыре составляющие тока:

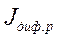– диффузионная составляющая дырочного тока;

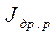– дрейфовая составляющая дырочного тока, равная по величине диффузионной и направленная противоположно;

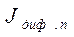– диффузионная составляющая электронного тока;

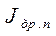– дрейфовая составляющая электронного тока, равная по величине диффузионной и направленная противоположно.

В сумме все четыре составляющие равны нулю:

.

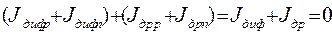Следовательно, p-n переход находится в состоянии термодинамического равновесия.

Наличие электрического поля в p-n переходе приводит к тому, что область объемного заряда оказывается обедненной носителями тока: поле выталкивает из области электроны и дырки. Поэтому концентрация подвижных носителей заряда в p-n переходе резко уменьшается. 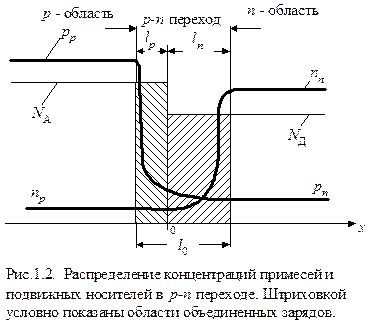Пониженная концентрация подвижных носителей обусловливает высокое сопротивление p-n перехода. В некотором сечении области объемного заряда (рис.1.2) концентрация электронов и дырок оказываются, равными. На основании условия:

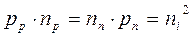(1.1)

в этом сечении концентрации электронов и дырок принимают значение, равное n_i – концентрации электронов в чистом беспримесном полупроводнике.

Зонная диаграммаp-n перехода. На рис. 1.3 изображены зонные диаграммы изолированных p и n полупроводников. Уровень Ферми у них расположен различно относительно границ запрещенной зоны.

Возникающая при контакте р и n полупроводников контактная разность потенциалов j_к приводит к взаимному смещению энергетичес­ких уровней в вертикальном направлении. Эти смещения таковы, что уровни Ферми двух областей теперь совпадают и изображаются на диаграмме перехода в виде одной горизонтальной линии. Физически это означает, что при образовании контакта между р и n областями происходит диффузионное перераспределение частиц до тех пор, пока средняя энергия заряженных частиц в обеих частях кристалла при тепловом равновесии не будет одинакова. Выравнивание уровней Ферми p и n областей ана­логично выравниванию уровней жидкости в сообщающихся сосудах и объясняется стремлением к минимуму потенциальной энергии любой системы. В области контакта происходит искривление энергетических уровней. Зонная диаграмма p-n перехода показана на рис. 1.4. С увеличением концентрации примесей N_Аи N_Дуровень Ферми будет смещаться к потолку валентной зоны в p области и к дну зоны проводимости в n области. Поэтому в предельном случае контактная разность потенциалов получается равной ширине запрещенной зоны. Использовать контактную разность потенциалов как источник э.д.с. не удается: при присоединении p-n перехода к внешней, цепи неизбеж­но возникают другие контактные разности потенциалов и общая э.д.с. в цепи оказывается равной нулю до тех пор, пока температура всех частей цепи поддерживается одинаковой.

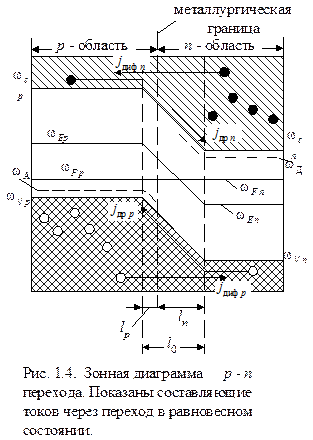На зонной диаграмме (рис. 1.4) показаны четыре составляющие тока через переход. Диффузионная составляющая электронного тока обуслов­лена электронами зоны проводимости n полупроводника, которые зани­мают энергетические уровни, лежащие выше уровня дна зоны проводимос­ти р полупроводника. Движение электронов из зоны проводимости р полупроводника в зону проводимости n полупроводника дает дрейфовую составляющую тока, компенсирующую диффузионную. Аналогично дырки, занимающие энергетические уровни, лежащие ниже уровня потолка валентной зоны n полупроводника, образуют диффузионную составляю­щую дырочного тока. Она уравновешивается дрейфовой составляющей тока дырок, двигающихся в обратном направлении - из валентной зоны n об­ласти в валентную зону р области.

Из рис. 1.4 видно, что в некотором сечении уровень Ферми оказывается расположенным точно посредине запрещенной зоны. Здесь p-п полупроводник обладает свойствами беспримесного (уро­вень Ферми в беспримесном полупроводнике лежит посредине запрещенной зоны) и имеет повышенное по сравнению с остальным объемом сопротив­ление.

Типы р-п переходов. Переходы бывают симметричными и несимметричными, резкими (ступенчатыми) и плавными.

В симметричном p-n переходе концентрации примесей в p и n областях почти одинаковые и имеет место соотношение p_p » n_n. Такие переходы не являются типичными. Гораздо чаще используются несимметричные переходы, в которых,

N_А>> N_Д (p_p >> n_n) или N_Д >> N_А (n_n >> p_p). Различие в концент­рациях примесей составляет до 1001000 раз.

Резким переходом называется такой, в котором толщина области изменения концентрации примесей значительно меньше толщины области объемного заряда. Под плавным переходом понимается переход, в котором толщина области изменения концентрации примесей сравнима с толщиной слоя объемного заряда. На рис. 1.2 дан пример резкого перехода. На практике резкие переходы являются определенным приближением. Однако они хорошо отра­жают свойства многих реальных p-n структур и, кроме того, проще для анализа. Поэтому ниже будут рассматриваться, в основном, резкие (ступенчатые) р-п переходы. Процессы, происходящие в плавных перехо­дах, качественно остаются теми же.

Анализ резкого р-п перехода в равновесном состоянии. Для упрощения анализа предположим, что концентрации подвижных носителей внутри перехода равны нулю, а вне перехода они считаются равновесными. В этом случае электрическое поле будет ограничено областью перехода. Структура та­кого идеализированного несимметричного перехода изображена на рис. 1.5.

Определим контактную разность потенциалов j_к0. Из рис. 1.4 следует, что

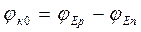, (1.2)

где j_E – электростатический потенциал полупроводника (потенциал соответствующий средине запрещенной зоны). Концентрации электронов n_n и дырок p_p определяются через потенциалы Ферми j_Fn и j_Fp и электростатический потенциал

, ,

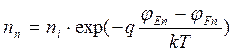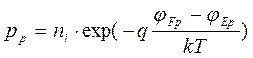где k- постоянная Больцмана, T- абсолютная температура, q- заряд электрона. Из этих выражений путем логарифмирования оп­ределим j_Ep и j_En и, учитывая, что j_Fp=j_Fn на основании (1.2 ) получим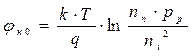

или с учётом (1.1)

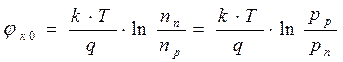(1.3 )

Из выражения (1.3) следует вывод, что j_к0 определяется пере­падом концентраций одноименных носителей заряда.

Типичной высотой потенциального барьера для германиевого пере­хода является j_к0 » 0.4В, а для кремниевого j_к0 » 0.7В. Последнее обусловлено более широкой запрещенной зоной кремния.

Поле в р-п переходе определяется на основании уравнения Пуассона:

,

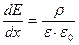где r - объемная плотность заряда, e₀- диэлектрическая проницаемость вакуума, e - относительная диэлектрическая проницаемость.

Плотности заряда в p и n областях резкого перехода соответственно равны (рис. 1.5 б).

где l _p - протяженность области объемного заряда в p полупроводнике, а l _n - в

n полупроводнике. После подстановки значения r в уравнение Пуассона и интегрирования в соответствующих пределах получаем:

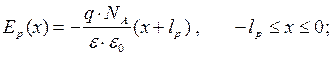(1.4 а)

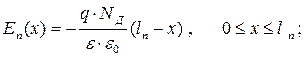(1.4 б)

E = 0 при других x . (1.4 в)

График распределения поля в переходе показан на рис. 1.5 в. Закон изменения потенциала j(x) в переходе определяется интегрированием выражений (1.4) при граничных, условиях:

j _p (x) = j _{E p} , x £ - l _p; j _n (x) = j _{E n} , x ³ l _n.

Тогда:

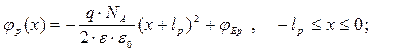(1.5a)

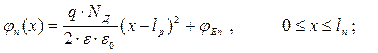(1.5б)

График изменения потенциала показан на рис. 1.5г. Приравнивая E_p(0) и E_n(0) найдем: 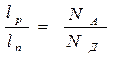. (1.6 )

Из (1.6 ) следует, что в симметричном переходе l_p = l_n , а в несим­метричном

– l_p ¹ l_n . Так, при N_А>> N_Д , l_p << l_n т.е. р-n переход будет сосредоточен в основном в n области или в более высокоомной части кристалла.

Из равенства j_p(0) = j_n(0) с учетом (1.2 ), (1.6 ) и того, что l_p + l_n = l₀ получим:

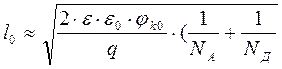(1.7)

В случае несимметричного перехода при N_А>> N_Д ,

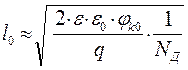
(1.8)