Поглощение света 2 страница

Окончательно получаем 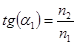 , где
, где  — угол Брюстера, для которого
— угол Брюстера, для которого 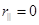 .
.
Коэффициенты отражения и пропускания света по энергии.
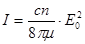 — интенсивность света.
— интенсивность света.
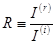 — энергетический коэффициент отражения
— энергетический коэффициент отражения
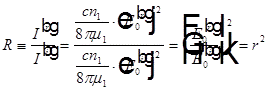
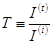 — энергетический коэффициент пропускания
— энергетический коэффициент пропускания
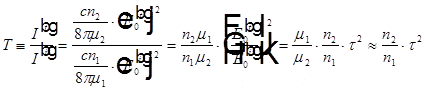
Окончательно получаем:
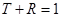
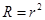
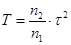
Потеря полуволны при отражении от оптически более плотной среды (  ).
).
Рассмотрим нормальное падение света на границу раздела двух сред, тогда 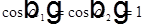 =>
=>  при условии отражения от оптически более плотной среды
при условии отражения от оптически более плотной среды  .
.
Отраженная волна имеет отрицательную амплитуду, но 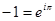 , следовательно, можно сказать, что отраженная волна сдвинута по фазе на
, следовательно, можно сказать, что отраженная волна сдвинута по фазе на  .
.
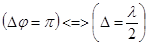 — сдвиг фазы на
— сдвиг фазы на  эквивалентен изменению длины пути на
эквивалентен изменению длины пути на  , что эквивалентно потери полуволны.
, что эквивалентно потери полуволны.
Рассмотрев графики зависимостей  от
от 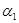 и
и 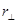 от
от 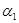 , можно сделать вывод, о противофазности отраженной и падающей волн при отражении света от оптически более плотной среды при любом угле падения и любой поляризации света.
, можно сделать вывод, о противофазности отраженной и падающей волн при отражении света от оптически более плотной среды при любом угле падения и любой поляризации света.
Отражение радиоволн от поверхности проводника.
Излучение диполя и диполя-изображения.
При скользящем падении излучения на зеркальную поверхность в случае, когда плоскость поляризации совпадает с плоскостью падения, радиоволны отражаются в фазе с падающей волной, а световые волны — в противофазе.
Отражение света при скользящем падении. Зеркало рентгеновского телескопа.
При скользящем падении света  =>
=>  =>
=>
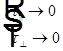 =>
=> 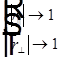 =>
=>  для любой поляризации при скользящем падении света.
для любой поляризации при скользящем падении света.
Полное внутреннее отражение и неоднородная волна.
Закон Снеллиуса 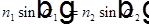 не имеет решения относительно
не имеет решения относительно  при условии
при условии 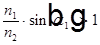 . Это и есть полное внутреннее отражение. Волна под границей раздела сред все же есть, так как иначе не удовлетворить граничным условиям для полей E и B.
. Это и есть полное внутреннее отражение. Волна под границей раздела сред все же есть, так как иначе не удовлетворить граничным условиям для полей E и B.
Пространственная частота трех волн на границе раздела сред должна быть одинаковой, иначе не удовлетворить граничным условиям сразу во всех точках границы. Пусть ось z перпендикулярна границе и световая волна падает в плоскости x,z. Тогда  . Но из
. Но из 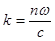 следует
следует 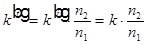 , откуда
, откуда 
Рассмотрим комплексное выражение для плоской волны под границей раздела сред и подставим в него полученные выражения для  и
и 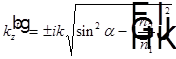 .
.
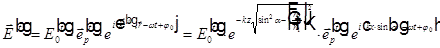 ,
,
Здесь
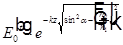 — амплитуда неоднородной плоской волны. Знак в показателе экспоненты выбран так, чтобы амплитуда убывала при удалении от границы раздела сред.
— амплитуда неоднородной плоской волны. Знак в показателе экспоненты выбран так, чтобы амплитуда убывала при удалении от границы раздела сред.
Экспериментальное наблюдение неоднородной плоской волны.
Люминесценция — любое нетепловое свечение,
хемилюминесценция — свечение в результате химической реакции,
электролюминесценция — свечение под действием электротока,
фотолюминесценция — свечение после освещения внешним источником света, иногда на другой частоте,
флюоресценция — кратковременная фотолюминесценция,
фосфоресценция — долговременная фотолюминесценция.
Фазовый сдвиг при полном внутреннем отражении.
При полном внутреннем отражении нет вещественного решения уравнения Снеллиуса 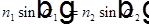
относительно угла преломления  , но комплексное решение есть:
, но комплексное решение есть:

Это значение косинуса угла преломления можно подставить в формулы Френеля и получить комплексные выражения для амплитудных коэффициентов отражения двух поляризаций света:
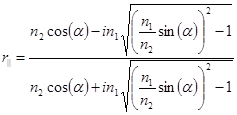 ,
,
 .
.
Заметим, что при полном внутреннем отражении отражается вся энергия: 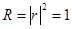 .
.
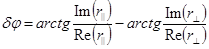 — сдвиг фаз между двумя линейными поляризациями отраженных волн.
— сдвиг фаз между двумя линейными поляризациями отраженных волн.
Параллелепипед Френеля.
За два полных внутренних отражения можно набрать сдвиг фаз  , что позволяет получить циркулярно поляризованный свет из света линейной поляризации.
, что позволяет получить циркулярно поляризованный свет из света линейной поляризации.
Полное внутреннее отражение в 450-ой стеклянной призме. Условие отражения без потерь.
Для полного внутреннего отражения без потерь поверхность должна быть чистой.
Уголковый отражатель. Измерение расстояния от Земли до Луны.
Уголковый отражатель — три взаимно перпендикулярные зеркальные плоскости, образующие внутренность угла куба.
Уголковый отражатель забросили на Луну. Измеряют время распространения светового импульса туда и обратно.
Оптический контакт. Светоделительный куб.
Если расстояние между двумя кусками одного и того же материала заметно меньше  , то эта граница не отражает свет. Это и есть оптический контакт.
, то эта граница не отражает свет. Это и есть оптический контакт.
В светоделительном кубе расстояние между двумя стеклянными призмами подбирают так, чтобы половина света отражалась от границы двух призм и половина проходила сквозь границу.
Тема 5. Кристаллооптика.
Факультативно. Механизм замедления света в среде.
Свет, проходя через среду, раскачивает электрические диполи атомов. Излучение диполей складывается с проходящей мимо световой волной, в результате сложения получается волна с измененной фазой. Изменение фазы относительно волны в вакууме означает другую фазовую скорость света в среде. В анизотропной среде для разных направлений вектора 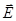 различается величина наведенного электрического диполя и изменение фазы световой волны. В результате оказывается, что скорость света в кристалле зависит не от направления луча, а от направления вектора
различается величина наведенного электрического диполя и изменение фазы световой волны. В результате оказывается, что скорость света в кристалле зависит не от направления луча, а от направления вектора 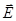 в световой волне.
в световой волне.
Факультативно. Главные диэлектрические оси кристалла.
По определению вектора электрической индукции  , где
, где 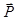 — поляризация среды или объемная плотность дипольного момента. Если дипольные моменты пропорциональны полю
— поляризация среды или объемная плотность дипольного момента. Если дипольные моменты пропорциональны полю 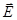 , то и вектор
, то и вектор  пропорционален
пропорционален 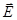 . Для анизотропной среды коэффициент пропорциональности является симметричной матрицей
. Для анизотропной среды коэффициент пропорциональности является симметричной матрицей 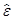 .
.
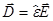 или
или 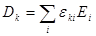 , где
, где 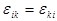 — условие симметричности матрицы
— условие симметричности матрицы 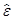 .
.
Поворотом системы координат симметричную матрицу всегда можно привести к диагональному виду: 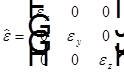 .
.
Оси, в которых матрица 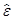 — диагональная называются главными диэлектрическими осями кристалла. Не путать с осями кристалла, о которых речь пойдет ниже.
— диагональная называются главными диэлектрическими осями кристалла. Не путать с осями кристалла, о которых речь пойдет ниже.
Факультативно. Аналог волнового уравнения в кристалле.
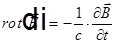 =>
=>
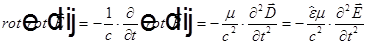 , но
, но
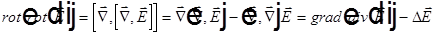 , тогда
, тогда
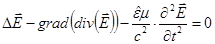
Направления векторов 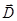 ,
, 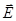 ,
, 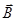 ,
,  ,
, 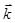 ,
, 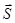 плоской световой волны в кристалле.
плоской световой волны в кристалле.
Для любой плоской волны  получаем
получаем  . Тогда уравнения Максвелла
. Тогда уравнения Максвелла 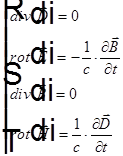 можно записать в виде
можно записать в виде 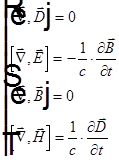 , откуда получаем
, откуда получаем  и, учитывая
и, учитывая 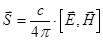 для вектора Пойнтинга, из трех последних равенств системы и равенства для вектора Пойнтинга получаем
для вектора Пойнтинга, из трех последних равенств системы и равенства для вектора Пойнтинга получаем 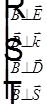 . Кроме того, из
. Кроме того, из 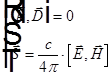 получаем
получаем 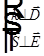 . Следовательно, тройка векторов
. Следовательно, тройка векторов 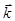 ,
,  ,
, 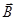 — взаимно ортогональна и тройка векторов
— взаимно ортогональна и тройка векторов 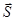 ,
, 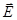 ,
, 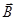 — взаимно ортогональна.
— взаимно ортогональна.
Тогда векторы 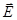 ,
,  ,
, 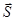 ,
, 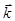 ортогональны вектору
ортогональны вектору 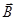 , а угол между векторами
, а угол между векторами 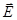 и
и  равен углу между векторами
равен углу между векторами 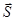 и
и 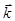 .
.
Лучевая и фазовая скорости световой волны в кристалле.
Обе скорости являются аналогом фазовой скорости света в изотропной среде. Лучевая скорость световой волны в кристалле 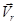 определяется направлением распространения энергии и совпадает с направлением вектора Пойнтинга
определяется направлением распространения энергии и совпадает с направлением вектора Пойнтинга 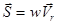 , где
, где 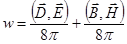 — объемная плотность энергии электромагнитного поля световой волны.
— объемная плотность энергии электромагнитного поля световой волны.
Фазовая скорость световой волны 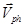 — скорость движения поверхности с постоянным значением фазы.
— скорость движения поверхности с постоянным значением фазы. 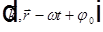 — фаза любой волны. Выберем ось z в направлении вектора
— фаза любой волны. Выберем ось z в направлении вектора 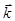 световой волны.
световой волны. 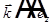 , тогда
, тогда  и уравнение постоянной фазы примет следующий вид
и уравнение постоянной фазы примет следующий вид 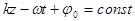 . Продифференцируем это уравнение по времени и получим
. Продифференцируем это уравнение по времени и получим 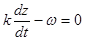 , откуда
, откуда 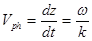 . Окончательно для фазовой скорости
. Окончательно для фазовой скорости
 и
и 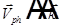 .
.
Рассматривая перемещение поверхности равных фаз можно получить
 , где
, где 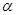 — угол между векторами
— угол между векторами 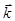 и
и 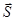 , и он же угол между векторами
, и он же угол между векторами  и
и 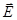 .
.
Факультативно. Величина лучевой и фазовой скорости в простейшем случае.
Простейший случай — это когда направление вектора 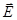 световой волны совпадает с одной из главных диэлектрических осей кристалла (пусть с осью x). В главных диэлектрических осях связь векторов
световой волны совпадает с одной из главных диэлектрических осей кристалла (пусть с осью x). В главных диэлектрических осях связь векторов  и
и 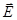 выглядит достаточно просто
выглядит достаточно просто  . Откуда получаем
. Откуда получаем  . Если вектор
. Если вектор 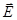 направлен вдоль оси x, то
направлен вдоль оси x, то  , откуда вектор
, откуда вектор  тоже имеет только составляющую
тоже имеет только составляющую  . Следовательно, в рассматриваемом случае векторы
. Следовательно, в рассматриваемом случае векторы  и
и 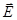 сонаправлены и кристаллическая среда ведет себя аналогично изотропной среды. Величина лучевой скорости в кристалле всегда зависит только от направления вектора
сонаправлены и кристаллическая среда ведет себя аналогично изотропной среды. Величина лучевой скорости в кристалле всегда зависит только от направления вектора 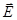 , а не от направления света. Тогда
, а не от направления света. Тогда 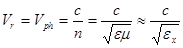 — лучевая и фазовая скорости совпадают по величине и направлению (угол между лучевой и фазовой скоростями равен углу между векторами
— лучевая и фазовая скорости совпадают по величине и направлению (угол между лучевой и фазовой скоростями равен углу между векторами  и
и 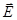 , который равен нулю).
, который равен нулю).
Фазовая пластинка.
Рассмотрим случай, когда свет распространяется вдоль одной из главных диэлектрических осей кристалла. Пусть  . Поскольку
. Поскольку 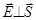 , вектор
, вектор 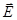 лежит в плоскости x,y. Разложим вектор
лежит в плоскости x,y. Разложим вектор 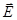 на составляющие вдоль осей x и y. Каждая из двух составляющих будет иметь вектор
на составляющие вдоль осей x и y. Каждая из двух составляющих будет иметь вектор 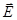 , направленный вдоль главной диэлектрической оси кристалла. Следовательно, каждая из двух составляющих поля будет иметь свою лучевую скорость, совпадающую с фазовой скоростью,
, направленный вдоль главной диэлектрической оси кристалла. Следовательно, каждая из двух составляющих поля будет иметь свою лучевую скорость, совпадающую с фазовой скоростью, 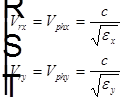 . Для этих двух лучей показатели преломления не равны
. Для этих двух лучей показатели преломления не равны 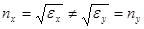 — двулучепреломление.
— двулучепреломление.
Фазовая пластинка — плоско параллельная кристаллическая пластинка, у которой две главные диэлектрические оси с различающимися диэлектрическими проницаемостями лежат в плоскости пластины.
Пластинки  и
и 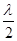 .
.
Фазовая пластинка с оптической разностью хода  для двух линейных поляризаций называется пластинкой
для двух линейных поляризаций называется пластинкой  .
.
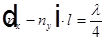
Для пластинки  разность хода —
разность хода —  и соответственно
и соответственно  .
.
Лучевой эллипсоид. Определение поляризации и лучевой скорости лучей по лучевому эллипсоиду (без доказательства).
Направим оси координат вдоль главных диэлектрических осей кристалла. Рассмотрим поверхность так называемого лучевого эллипсоида, уравнение которого 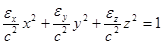 . Главные полуоси эллипсоида имеют длины
. Главные полуоси эллипсоида имеют длины  ,
,  ,
, 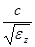 , равные лучевым скоростям, когда вектор
, равные лучевым скоростям, когда вектор 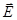 направлен вдоль соответствующих осей.
направлен вдоль соответствующих осей.
Алгоритм нахождения поляризаций двух световых волн для заданного направления луча 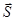 следующий.
следующий.  , поэтому векторы
, поэтому векторы 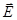 обеих волн лежат в плоскости перпендикулярной лучу. Рассмотрим сечение эллипсоида плоскостью перпендикулярной лучу
обеих волн лежат в плоскости перпендикулярной лучу. Рассмотрим сечение эллипсоида плоскостью перпендикулярной лучу 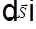 , проходящей через центр эллипсоида. Сечение эллипсоида — эллипс. Оси эллипса — направления вектора
, проходящей через центр эллипсоида. Сечение эллипсоида — эллипс. Оси эллипса — направления вектора 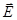 двух лучей. Длина полуосей эллипса — лучевые скорости двух лучей.
двух лучей. Длина полуосей эллипса — лучевые скорости двух лучей.
Оптическая ось кристалла (лучевая ось). Одноосные и двуосные кристаллы.
Нельзя путать оси кристалла с главными диэлектрическими осями кристалла.
Кристаллы называются одноосными, если  . Если
. Если  , то кристалл двуосный.
, то кристалл двуосный.
Направление луча, для которого лучевая скорость любой поляризации света одинакова, называется осью кристалла (оптической осью, лучевой осью).
Если  , то кристалл имеет две оси в плоскости x,z.
, то кристалл имеет две оси в плоскости x,z.
Обыкновенный и необыкновенный лучи.
В одноосном кристалле один луч обыкновенный, другой — необыкновенный. В двуосном кристалле оба луча необыкновенные.
Рассмотрим одноосный кристалл. Рассмотрим центральное сечение лучевого эллипсоида. Всегда одна из полуосей сечения перпендикулярна оси кристалла. Ее длина не зависит от направления плоскости сечения. Лучевая скорость соответствующего луча не зависит от направления луча. Это и есть обыкновенный луч. для луча этой поляризации кристалл изотропен.
Рассмотрим плоскопараллельную пластинку из одноосного кристалла. Пусть на пластинку под углом к нормали падает неполяризованный свет. При вращении пластинки вокруг нормали обыкновенный луч неподвижен, а необыкновенный луч на выходе из пластинки смещается параллельно самому себе.
Факультативно. Построение двойной лучевой поверхности с помощью лучевого эллипсоида.
Нельзя путать лучевую поверхность с рассмотренной ранее поверхностью лучевого эллипсоида.
Выберем в пространстве некоторую точку O, вокруг которой и будем строить лучевые поверхности. Для каждого направления луча отложим из одной и той же точки O два отрезка, равные лучевым скоростям двух лучей для выбранного направления луча. Величины лучевых скоростей двух лучей находятся как длины полуосей сечения лучевого эллипсоида плоскостью перпендикулярной выбранному направлению луча. Вторые концы двух отрезков при изменении направления луча образуют две лучевые поверхности.
Факультативно. Построения Гюйгенса в изотропной и анизотропной среде.
Лучевая скорость направлена в точку касания фронта волны лучевой поверхности.
Фазовая скорость направлена перпендикулярно фронту волны.
Поляризаторы на основе призмы Николя и Волластона.
Призма Николя. Две призмы из исландского шпата, склеены канадским бальзамом. 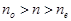 , где n — показатель преломления канадского бальзама. Свет одной из линейных поляризаций испытывает на границе полное внутреннее отражение и выходит из рассмотрения. Свет, проходящий сквозь границу, будет линейно поляризован и слегка ослаблен.
, где n — показатель преломления канадского бальзама. Свет одной из линейных поляризаций испытывает на границе полное внутреннее отражение и выходит из рассмотрения. Свет, проходящий сквозь границу, будет линейно поляризован и слегка ослаблен.
Призма Волластона состоит из двух призм, в которых направления оси кристалла ортогональны. На границе двух призм свет двух линейных поляризаций преломляется отклоняясь в разные стороны.
Тема 6. Геометрическая оптика.
Центрированные оптические системы, оптическая ось, параксиальная оптика.
Центрированная оптическая система — это система, в которой все преломляющие границы сферические, и центры всех сфер лежат на одной прямой.
Эта прямая называется оптической осью системы.
Приближение параксиальной оптики состоит в двух допущениях. Все лучи имеют малый угол с оптической осью. Каждый луч, проходя преломляющую границу, находится на малом расстоянии от оптической оси. Расстояние мало по сравнению с радиусом кривизны преломляющей поверхности.
Преломление света на сферической границе.
Пусть  ,
,  — угол между лучом и оптической осью до и после преломления на границе,
— угол между лучом и оптической осью до и после преломления на границе, 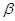 — угол между оптической осью и нормалью к границе в точке преломления луча. Тогда
— угол между оптической осью и нормалью к границе в точке преломления луча. Тогда 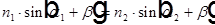 — закон Снеллиуса., где в приближении параксиальной оптики синусы можно опустить. Тогда
— закон Снеллиуса., где в приближении параксиальной оптики синусы можно опустить. Тогда 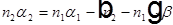 , где
, где 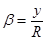 , где
, где 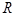 — радиус кривизны границы двух сред. Окончательно получаем
— радиус кривизны границы двух сред. Окончательно получаем
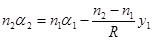
Матричная оптика. Опорная плоскость. Координаты луча.
Матрица трансляции. Матрица преломления на сферической границе.
Оптическая сила сферической границы.
Плоскость перпендикулярную оптической оси назовем опорной плоскостью.
Рассмотрим две опорные плоскости. Каждый луч в первой опорной плоскости будем характеризовать двумя координатами: расстояние 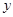 от оптической оси и произведение
от оптической оси и произведение  , где
, где  — показатель преломления в первой опорной плоскости,
— показатель преломления в первой опорной плоскости, 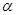 — угол между лучом и оптической осью. Из двух координат луча можно составить вектор
— угол между лучом и оптической осью. Из двух координат луча можно составить вектор 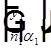 в некотором абстрактном пространстве. Здесь индекс 1 относится к первой опорной плоскости. Координаты луча во второй опорной плоскости, если между плоскостями однородная среда с показателем преломления
в некотором абстрактном пространстве. Здесь индекс 1 относится к первой опорной плоскости. Координаты луча во второй опорной плоскости, если между плоскостями однородная среда с показателем преломления  , можно найти из системы
, можно найти из системы  , где
, где  ,
, 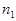 ,
,  — один и тот же показатель преломления среды между опорными плоскостями,
— один и тот же показатель преломления среды между опорными плоскостями, 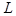 — расстояние между опорными плоскостями.
— расстояние между опорными плоскостями.
Тогда координаты луча во второй опорной плоскости можно выразить через координаты луча в первой опорной плоскости с помощью некоторой матрицы  :
:  , где
, где
 называется матрицей трансляции.
называется матрицей трансляции.
Для преломления на сферической границе  , где второе уравнение было получено в предыдущем вопросе. Тогда
, где второе уравнение было получено в предыдущем вопросе. Тогда
 — матрица преломления на сферической границе, где
— матрица преломления на сферической границе, где
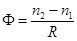 — оптическая сила сферической границы.
— оптическая сила сферической границы.
Заметим, что если рассмотреть три опорные плоскости, то  , так как каждая часть равенства
, так как каждая часть равенства 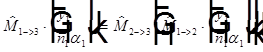 равна вектору
равна вектору 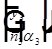 .
.
Дата добавления: 2015-06-12; просмотров: 1233;
