Поглощение света 4 страница
Угловая ширина дифракционного максимума решетки.
 , где N — число штрихов решетки, d — шаг решетки, D — ширина решетки.
, где N — число штрихов решетки, d — шаг решетки, D — ширина решетки.
Спектральное разрешение дифракционной решетки. Критерий Рэлея.
 , где m — порядок интерференции, N — число штрихов решетки.
, где m — порядок интерференции, N — число штрихов решетки.
Побочные максимумы дифракционной решетки.
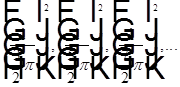 — относительные интенсивности побочных максимумов.
— относительные интенсивности побочных максимумов.
Условие отсутствия четных дифракционных максимумов решетки.
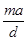 — целое число, это условие отсутствия главного максимума m-ого порядка, где
— целое число, это условие отсутствия главного максимума m-ого порядка, где  — ширина прозрачной части штриха.
— ширина прозрачной части штриха.
Дифракционная решетка с синусоидальным коэффициентом пропускания.
 , где
, где  и
и  .
.
Фазовая дифракционная решетка.

Отражательная дифракционная решетка.
Решетка с профилированным штрихом.
Тема 11. Голография.
Голограмма плоской световой волны.
Голограмма точки при нормальном падении опорной волны.
 =>
=>  =>
=>
При  :
:  ,
,
при 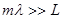 :
: 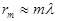 .
.
Голограмма точки при наклонном падении опорной волны.
Плоская голограмма протяженного объекта.
Толстослойная голограмма.
 =>
=> 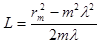 и
и  .
.
Пусть при записи голограммы  =>
=>  .
.
Пусть при воспроизведении голограммы 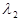 =>
=>
 =>
=>
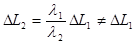 => мнимые изображения от разных слоев голограммы не совпадают при условии
=> мнимые изображения от разных слоев голограммы не совпадают при условии  .
.
Тема 12. Дифракционный предел разрешения.
Дифракционный предел разрешения телескопа и глаза.
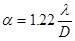 — угловое разрешение телескопа, где D — диаметр объектива телескопа.
— угловое разрешение телескопа, где D — диаметр объектива телескопа.
Понятие о разрешающей способности микроскопа.
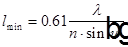 , где (2u) — апертура микроскопа, n — показатель преломления среды между предметом и объективом микроскопа.
, где (2u) — апертура микроскопа, n — показатель преломления среды между предметом и объективом микроскопа.
 — числовая апертура микроскопа.
— числовая апертура микроскопа.
Тема 13. Взаимодействие света с веществом.
Факультативно. Постановка задачи.
1. Реакция среды на поле световой волны, осциллирующие диполи атомов.
2. Обратное воздействие среды на волну, интерференция излучения диполей и проходящей световой волны. Изменение амплитуды в результате интерференции — поглощение света, изменение фазы — показатель преломления отличный от единицы.
Комплексная восприимчивость среды. Ее связь с коэффициентом поглощения и показателем преломления. Закон Бугера.
 , где
, где 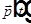 и
и  — комплексные дипольный момент атома и действующая на атом напряженность поля световой волны, α — комплексная поляризуемость атома.
— комплексные дипольный момент атома и действующая на атом напряженность поля световой волны, α — комплексная поляризуемость атома.
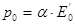 , где
, где  и
и 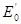 — комплексные амплитуды дипольного момента и напряженности поля.
— комплексные амплитуды дипольного момента и напряженности поля.
 , где
, где 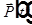 — комплексная поляризация среды,
— комплексная поляризация среды, 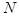 — концентрация атомов.
— концентрация атомов.
 , где
, где  — комплексная восприимчивость среды.
— комплексная восприимчивость среды.
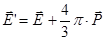 =>
=>  для не очень плотной среды.
для не очень плотной среды.
 , где
, где 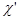 и
и  — вещественная и мнимая части комплексной восприимчивости среды.
— вещественная и мнимая части комплексной восприимчивости среды.
 для взаимодействия света со средой =>
для взаимодействия света со средой => 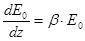 , где
, где  — какой-то коэффициент пропорциональности =>
— какой-то коэффициент пропорциональности => 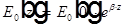
Плоская волна  описывает экспоненциальную зависимость комплексной амплитуды волны при комплексном волновом числе
описывает экспоненциальную зависимость комплексной амплитуды волны при комплексном волновом числе  .
.
Введем обозначения для вещественной и мнимой части комплексного  :
:
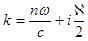
Тогда  . Здесь
. Здесь  — изменяющаяся с z координатой амплитуда поля.
— изменяющаяся с z координатой амплитуда поля.
Тогда интенсивность, как квадрат амплитуды, тоже изменяется по экспоненциальному закону  . Эта зависимость интенсивности света называется законом Бугера. Здесь
. Эта зависимость интенсивности света называется законом Бугера. Здесь  называется коэффициентом поглощения среды.
называется коэффициентом поглощения среды.
Мнимый показатель экспоненты в выражении для поля равен фазе волны 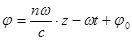 . Уравнение поверхности постоянной фазы
. Уравнение поверхности постоянной фазы 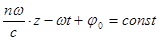 можно продифференцировать по времени и найти фазовую скорость или скорость движения поверхности постоянной фазы
можно продифференцировать по времени и найти фазовую скорость или скорость движения поверхности постоянной фазы 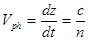 . Следовательно,
. Следовательно,  в выражении для вещественной части
в выражении для вещественной части  является показателем преломления среды по определению показателя преломления
является показателем преломления среды по определению показателя преломления  .
.
В уравнении Гельмгольца  для комплексной амплитуды поля
для комплексной амплитуды поля 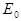 за
за  обозначено
обозначено  , но
, но  . Подставляя
. Подставляя 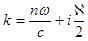 , получаем комплексное уравнение
, получаем комплексное уравнение 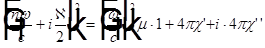 . Откуда находим вещественные
. Откуда находим вещественные  и
и  :
:


Для не слишком плотной среды, когда  , получаем
, получаем
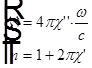
Модель атома Томсона. Комплексная поляризуемость атомов Томсона.
Комплексная восприимчивость среды из атомов Томсона.
 , где
, где  — радиус вектор проведенный из ядра атома к центру тяжести электронной оболочки,
— радиус вектор проведенный из ядра атома к центру тяжести электронной оболочки, 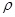 — плотность электронного облака,
— плотность электронного облака,  — полный заряд электронного облака,
— полный заряд электронного облака,  — масса электронного облака,
— масса электронного облака, 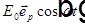 — внешнее световое поле. Умножив на заряд
— внешнее световое поле. Умножив на заряд  , добавив феноменологическое затухание и перейдя к комплексному выражению для поля, получаем дифференциальное уравнение для дипольного момента атома Томсона:
, добавив феноменологическое затухание и перейдя к комплексному выражению для поля, получаем дифференциальное уравнение для дипольного момента атома Томсона:
 , где
, где 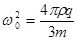 ,
, 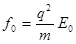 .
.
Стационарное решение этого уравнения имеет вид 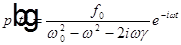 . Сравнивая с
. Сравнивая с  , находим комплексную поляризуемость атома Томсона:
, находим комплексную поляризуемость атома Томсона: 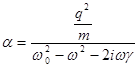 и комплексную восприимчивость среды
и комплексную восприимчивость среды 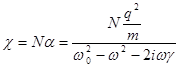 .
.
При малых отстройках  частоты света
частоты света  относительно частоты поглощения
относительно частоты поглощения  получаем для вещественной и мнимой части восприимчивости среды выражения:
получаем для вещественной и мнимой части восприимчивости среды выражения:
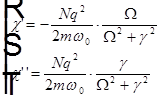 и с учетом
и с учетом 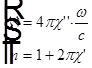 получаем
получаем
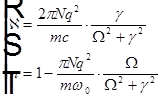 , где
, где  — отстройка частоты светового поля относительно частоты поглощающего перехода,
— отстройка частоты светового поля относительно частоты поглощающего перехода, 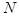 — концентрация атомов.
— концентрация атомов.
Нормальная и аномальная дисперсия света.
Причина неравенства n > 1 в частотной области прозрачности среды.
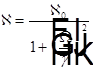 — лоренцевский контур линии поглощения среды,
— лоренцевский контур линии поглощения среды, 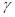 — полуширина на полувысоте линии поглощения.
— полуширина на полувысоте линии поглощения.
 — дисперсионный контур показателя преломления среды.
— дисперсионный контур показателя преломления среды.
 — нормальная дисперсия,
— нормальная дисперсия,
 — аномальная дисперсия.
— аномальная дисперсия.
Факультативно. Интегральное соотношение между вещественной
и мнимой частями амплитудного коэффициента пропускания.
Дисперсионное соотношение Крамерса-Кронига.
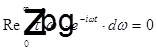 при t < 0, где
при t < 0, где  — амплитудный коэффициент пропускания.
— амплитудный коэффициент пропускания.
 при t < 0.
при t < 0.
 при t < 0.
при t < 0.
 — соотношения Крамерса-Кронига, здесь
— соотношения Крамерса-Кронига, здесь  — главное значение интеграла.
— главное значение интеграла.
Рассеяние света.
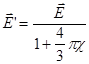 — поле внутри капли тумана.
— поле внутри капли тумана.
 — поляризация капли.
— поляризация капли.
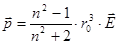 — дипольный момент капли,
— дипольный момент капли,  — радиус капли,
— радиус капли,  — показатель преломления капли.
— показатель преломления капли.
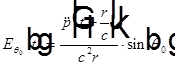 — поле излучения диполя, где
— поле излучения диполя, где  — угол между направлением колебаний диполя и направлением излучения.
— угол между направлением колебаний диполя и направлением излучения.
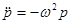

Пусть  — угол рассеяния, тогда для одной поляризации света
— угол рассеяния, тогда для одной поляризации света 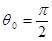 независимо от величины
независимо от величины  , для другой поляризации
, для другой поляризации  . Откуда
. Откуда
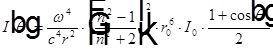 , где
, где  — интенсивность света рассеянного одно каплей тумана,
— интенсивность света рассеянного одно каплей тумана,  — радиус капли,
— радиус капли, 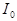 — интенсивность неполяризованного падающего света,
— интенсивность неполяризованного падающего света,  — угол рассеяния.
— угол рассеяния.
Рэлеевское рассеяние света.
 , где
, где  — поляризуемость атомов,
— поляризуемость атомов,  — количество атомов в объеме
— количество атомов в объеме 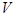 .
.
Волна де Бройля. Уровни энергии атома водорода.
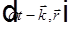 — скаляр по группе Лоренца для любой волны,
— скаляр по группе Лоренца для любой волны, 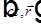 — 4-х вектор, тогда
— 4-х вектор, тогда
 — 4-х вектор.
— 4-х вектор.
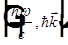 — 4-х вектор для любой волны,
— 4-х вектор для любой волны,
 — 4-х вектор для любой частицы.
— 4-х вектор для любой частицы.
Де Бройль предположил, что каждой частице соответствует волна и эти два 4-х вектора совпадают.
Тогда  , откуда
, откуда  — длина волны де Бройля, где
— длина волны де Бройля, где  — импульс частицы.
— импульс частицы.
 , где
, где 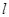 — длина замкнутой траектории,
— длина замкнутой траектории,  — целое число.
— целое число.
Тогда для атома водорода
 =>
=>  =>
=> 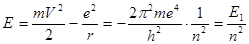 — уровни энергии атома водорода.
— уровни энергии атома водорода.
Частота перехода между уровнями энергии.
Пусть атом находится одновременно на двух уровнях энергии с волновыми функциями состояний  и
и  . Тогда суммарная волновая функция
. Тогда суммарная волновая функция 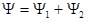 испытывает биения на частоте
испытывает биения на частоте  . Плотность электронного облака в каждой точке испытывает биения с частотой
. Плотность электронного облака в каждой точке испытывает биения с частотой 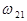 , дипольный момент атома осциллирует с частотой
, дипольный момент атома осциллирует с частотой 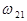 , атом излучает поле с частотой
, атом излучает поле с частотой 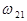 .
.
При излучении света атом теряет порцию энергии 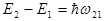 . Отсюда следует, что свет излучается и поглощается порциями
. Отсюда следует, что свет излучается и поглощается порциями  .
.
Факультативно. Разрешенные и запрещенные переходы. Правила отбора.
Поглощение света. Вынужденное излучение света. Спонтанное излучение света.
Факультативно. Понятие о коэффициентах Эйнштейна.
Инверсия заселенностей лазерной среды.
 , где
, где 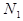 — заселенность уровня 1,
— заселенность уровня 1,  — вероятность обнаружить атом на уровне 1,
— вероятность обнаружить атом на уровне 1, 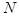 — концентрация атомов.
— концентрация атомов.
По распределению Больцмана 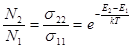 при термодинамическом равновесии при температуре T. В этом случае N2 < N1 при E2 > E1.
при термодинамическом равновесии при температуре T. В этом случае N2 < N1 при E2 > E1.
Если равновесия нет, то возможна ситуация, при которой N2 > N1 — инверсия заселенностей.
Факультативно. Необязательность модели атома Томсона
для лоренцевского контура линии поглощения
и дисперсионного контура показателя преломления.
Пусть  при t > 0.
при t > 0.
Тогда 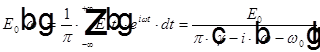 — Фурье-образ поля.
— Фурье-образ поля.
 =>
=>  — лоренцевский контур линии спонтанного излучения. Для сохранения распределения Больцмана в условиях термодинамического равновесия необходимо, чтобы контуры линии поглощения и линии вынужденного излучения были подобны контуру линии спонтанного излучения.
— лоренцевский контур линии спонтанного излучения. Для сохранения распределения Больцмана в условиях термодинамического равновесия необходимо, чтобы контуры линии поглощения и линии вынужденного излучения были подобны контуру линии спонтанного излучения.
Дисперсионный контур показателя преломления следует из соотношения Крамерса-Кронига.
Рентгеновское излучение. Сплошной и линейчатый спектры излучения рентгеновской трубки. K, L, M, N, O, ... - серии рентгеновских спектральных линий.
Дифракция рентгеновских лучей на кристалле. Лауэграммы.
 ,
,
где 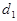 — пространственный период решетки,
— пространственный период решетки,  — целое число,
— целое число, 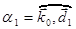 ,
, 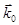 — волновой вектор падающей волны,
— волновой вектор падающей волны, 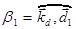 ,
,  — волновой вектор дифрагирующей волны.
— волновой вектор дифрагирующей волны.
Условие Вульфа-Брегга
для дифракции монохроматических рентгеновских лучей на поликристалле.
 , где
, где  — разность хода,
— разность хода,  — межплоскостное расстояние,
— межплоскостное расстояние,  — угол скольжения,
— угол скольжения,  — целое число.
— целое число.
Эффект Комптона.
Эффект Комптона — рассеяние рентгеновского излучения с изменением длины волны рассеянного излучения.
Рассмотрение эффекта проводится в нерелятивистском приближении, так как энергия фотона гораздо меньше энергии покоя электрона: 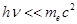 .
.
Для фотона 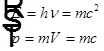 =>
=> 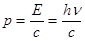 — импульс фотона.
— импульс фотона.
Для рассеяния фотона на свободном электроне напишем закон сохранения энергии и закон сохранения импульса для двух проекций импульса:
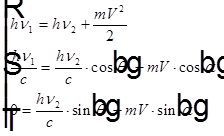
Решаем эту систему относительно неизвестных 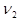 ,
, 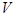 ,
,  . Угол рассеяния фотона
. Угол рассеяния фотона  — параметр задачи.
— параметр задачи.
Исключаем  из второго и третьего уравнений системы и получаем
из второго и третьего уравнений системы и получаем
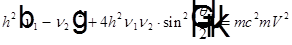
Из первого уравнения системы получаем 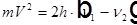 , что можно подставить в предыдущее уравнение и получить:
, что можно подставить в предыдущее уравнение и получить:

Здесь первым слагаемым можно пренебречь, так как  =>
=> 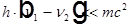 =>
=> 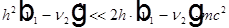 . В результате пренебрежения получаем:
. В результате пренебрежения получаем:
 . Разделим это равенство на
. Разделим это равенство на  и получим окончательное выражение для изменения длины волны рассеянного рентгеновского излучения в зависимости от направления рассеяния
и получим окончательное выражение для изменения длины волны рассеянного рентгеновского излучения в зависимости от направления рассеяния

Световое давление. Корпускулярная и волновая трактовки светового давления.
1). Корпускулярная трактовка.
Для фотона 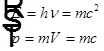 =>
=>  — связь импульса фотона и его энергии.
— связь импульса фотона и его энергии.
Давление по определению 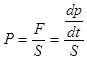 . Следовательно, давление — плотность потока импульса.
. Следовательно, давление — плотность потока импульса.
Интенсивность света 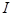 — плотность потока энергии. Следовательно
— плотность потока энергии. Следовательно
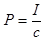 — выражение для давления света через интенсивность света.
— выражение для давления света через интенсивность света.
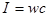 , где
, где  — объемная плотность энергии светового поля, тогда
— объемная плотность энергии светового поля, тогда 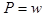 .
.
2). Волновая трактовка.
Давление создается силой Лоренца со стороны магнитного поля световой волны, действующей на заряды электрического тока, вызванного электрическим полем световой волны.
Фотоэффект. Красная граница фотоэффекта. Формула Эйнштейна. Опыты Столетова.
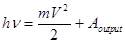 , где
, где  — масса выбиваемого электрона,
— масса выбиваемого электрона, 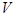 — его скорость,
— его скорость, 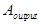 — работа выхода.
— работа выхода.
 — красная граница фотоэффекта.
— красная граница фотоэффекта.
Факультативно. Внутренний фотоэффект. Фотодиод.
Доплеровский контур линии поглощения.
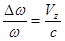 — продольный эффект Доплера, где
— продольный эффект Доплера, где  — проекция скорости молекул на луч или лучевая скорость. Тогда
— проекция скорости молекул на луч или лучевая скорость. Тогда
 , где
, где  — частота света в системе отсчета молекулы,
— частота света в системе отсчета молекулы,  — частота света в лабораторной системе отсчета,
— частота света в лабораторной системе отсчета,  — волновое число.
— волновое число.
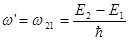 — условие резонансного поглощения света.
— условие резонансного поглощения света.
Следовательно 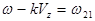 =>
=> 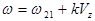 . Чем больше молекул имеет лучевую скорость
. Чем больше молекул имеет лучевую скорость  , тем больше поглощение света на частоте
, тем больше поглощение света на частоте  . Контур линии поглощения повторяет распределение Максвелла по проекции скорости молекул на луч:
. Контур линии поглощения повторяет распределение Максвелла по проекции скорости молекул на луч:
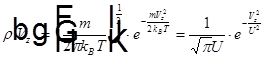 , где
, где 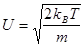 — наиболее вероятная скорость молекул газа.
— наиболее вероятная скорость молекул газа.
Заменяем в этом распределении  на
на  и получаем доплеровский контур линии поглощения:
и получаем доплеровский контур линии поглощения:
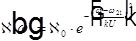
Лазерное охлаждение.
Дата добавления: 2015-06-12; просмотров: 959;
