Частные решения волнового уравнения.

Разделение временной и пространственных переменных решения волнового уравнения

.

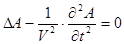Пусть

,

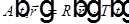подставим в волновое уравнение для A и разделим уравнение на RT, тогда одно слагаемое зависит только от , а другое — только от t. Следовательно, каждое из двух слагаемых равно константе, которую обозначим за .

Тогда для функции координат получим

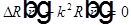— уравнение Гельмгольца, а для функции времени

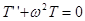— уравнение гармонических колебаний,

где .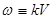

Разделение переменных решения уравнения Гельмгольца в декартовых координатах, пусть

.

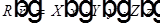Подставим это решение в уравнение Гельмгольца и разделим его на произведение XYZ. При этом слагаемые уравнения окажутся функциями разных переменных и, следовательно, каждое слагаемое — константа:

, , ,

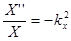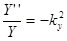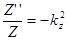где .

Решения для X, Y, Z — гармонические колебания от x, y, z.

Подставляя решения для X, Y, Z в R, а затем решения для R и T в A, получаем — решение в комплексной форме в виде плоских волн

.

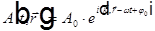Разделение переменных в других системах координат приводит к другим решениям. Среди множества решений в цилиндрической системе координат отметим решение в виде цилиндрической волны

,

Где

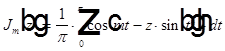— функция Бесселя с целым значком

Среди множества решений в сферической системе координат отметим решение в виде сферической волны

.