Основные сведения

В диапазоне ОВЧ и выше условие квазистационарности не выполняется, и ЭМП проявляет волновой характер [33, 37].

Для расчетов УВЧ и СВЧ многополюсников (рис. 20.1) обычно используют волновые матрицы, связывающие приведенные напряжения падающих и отраженных волн на входах многополюсника.

Под приведенным напряжениемV, характеризующим энергетические соотношения ЭМВ в плечах многополюсника, понимают напряжение U в ЛП, деленное на ее :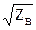

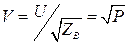[37]

Матрицы сопротивлений (Z-матрица) и проводимости (Y-матрица) выражают связь напряжений и токов многополюсника :

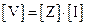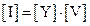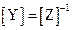; ; , (20.1)

Для четырехполюсников (элементы Z-матрицы определяются при холостом ходе, а Y-матрицы – при коротком замыкании входов) [37]:

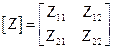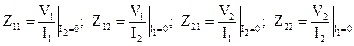; . (20.2)

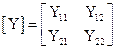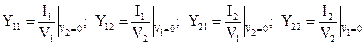; . (20.3)

Достоинством Z- и Y-матрицы является возможность простого представления сосредоточенных нерегулярностей в регулярной ЛП [2].

Волновой характер ЭМП в диапазонах УВЧ и СВЧ затрудняет применение Z- и Y-матриц из-за явления трансформации сопротивлений и проводимостей в ЛП. Эти матрицы могут быть рассчитаны только для определенных сечений ЛП, и при неудачном выборе плоскости отсчета элементы матриц могут принимать бесконечно большие значения.

Поэтому для анализа удобно использовать матрицы с волновыми величинами, которые не изменяют свой модуль в ЛП без потерь [2, 37].

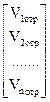
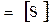
Такими матрицами являются матрица рассеяния (S-матрица) и матрица передачи (T-матрица). Используя элементы волновой матрицы рассеяния (S-параметры), связь между приведенными напряжениями падающих и отраженных волн можно представить в следующем ви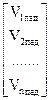де:

, где 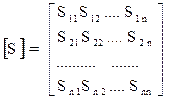. (20.4)

Элементы S-матрицы имеют ясный физический смысл: S_ii является коэффициентом отражения i-го плеча, а S_ki (при i ¹ k) – коэффициентом передачи с i-го входа на k-й выход по приведенному напряжению V.

Если S-матрица устройства известна, то можно считать, что оно описано полностью [2, 33, 37]. Значения элементов матрицы рассеяния могут быть определены экспериментально. Элементы матрицы рассеяния не зависят от того, какие в дальнейшем внешние нагрузки и источники будут подключаться к плечам. S-матрица изменяется только со сменой типа волны или значений параметров элементов.

Во взаимных устройствах с линейными изотропными средами матрица рассеяния симметрична: S_ki = S_ik [37]. Важными являются следующие свойства S-матрицы для пассивных устройств без потерь [37]:

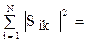
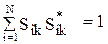; (20.5)

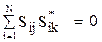. (20.6)

Свойство (20.5) выражает закон сохранения энергии.

S-матрица, удовлетворяющая условиям (20.5) и (20.6), называется унитарной. Число ее независимых элементов составляет N(N+1)/2, а для взаимных устройств: N(N–1)/2.

В технике УВЧ и СВЧ широко распространены четырехполюсники, которым соответствует матрица рассеяния

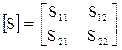. (20.7)

Элементы этой матрицы (S-параметры) принято называть так: S₁₁ и S₂₂ -коэффициент отражения от входа и выхода соответственно; S₂₁ - коэффициент прямой передачи; S₁₂ -коэффициент обратной передачи.

В случае взаимного устройства без потерь у матрицы (20.7) будет только один независимый элемент. Связывая S-параметры (20.7) между собой с помощью (20.5) и (20.6), получим

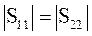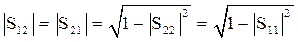; . (20.8)

При каскадном соединении многополюсников итоговая матрица рассеяния не может быть получена простым перемножением матриц БЭ. В этом случае удобно использовать матрицу передачи (T-матрицу), которая не имеет данного недостатка. При расчетах каскадного соединения четырехполюсников с матрицами передачи [T₁][T₂],…,[T_n] результирующая матрица передачи равна произведению их матриц передачи: [T_S]=[T₁]×[T₂]×…×[T_n]. Элементы [S] и [T] матриц связаны так [37]:

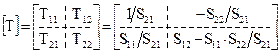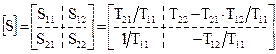; . (20.9)

При объединении S-матриц каскадного соединения четырехполюсников возможен переход от S-матриц к T-матрицам (20.9), а после получения итоговой T-матрицы – обратный переход к матрице рассеяния.

Аналогичная связь S-матрицы с Z- и Y-матрицами определяется так:

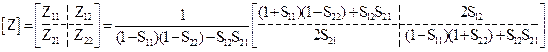; (20.10)

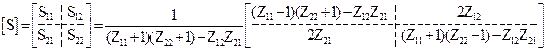. (20.11)

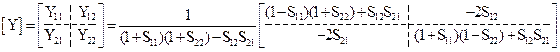; (20.12)

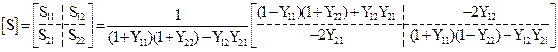. (20.13)

Переход от S-матрицы к T, Z и Y-матрицам и обратно возможен не всегда. Математически условия допустимости преобразований (20.9)- (20.13) можно сформулировать так: знаменатель общего множителя в соответствующей формуле должен иметь ненулевое значение.

Методы анализа многоэлементных устройств СВЧ основаны на расчленении (декомпозиции) сложного объекта на отдельные более простые, S-матрицы которых могут быть рассчитаны сравнительно просто. Затем по определенным алгоритмам (рекомпозиция) находится S-матрица устройства в целом.

ЭМВ в ЛП возбуждают с помощью штырей, петель связи, отверстий связи и т. п. В каждом случае оптимальное место ввода устройства возбуждения строго определено [2, 33].

Нерегулярности в волноводе.Рассмотрим диафрагмы в прямоугольном волноводе (рис. 20.2). Эти диафрагмы вносят в ЭМП реактивность, которую учитывают как сосредоточенную нерегулярность, вклю­ченную параллельно в регулярную ЛП [22].

Тонкая индуктивная диафрагма (рис. 20.3) образована металлическими пластинами, примыкающими к узкой стенке волновода. Так как вблизи стенок локализуется магнитное поле волны H₁₀, диафрагма возмущает преимущественно это поле и ее эквивалентная проводимость имеет индуктивный характер.

Эквивалентная индуктивность диафрагмы вычисляется так:

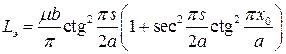. (20.14)

Симметричная (x0 = a/2) индуктивная диафрагма при m = 1 и a » 2b вносит параллельную реактивную проводимость в ЛП

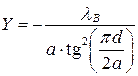. (20.15)

В тонкой емкостной диафрагме (рис. 20.4) металлические пластины примыкают к широкой стенке и возмущают в основном электрическое поле волны H₁₀. Эквивалентная шунтирующая емкость определяется так:

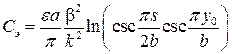. (20.16)

Симметричная емкостная диафрагма (y0 = b/2 при e=1) вносит параллельную реактивную проводимость в ЛП

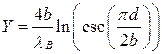. (20.17)

Модуль коэффициента отражения Г, вносимого данными L и C диафрагмами, при нормированных проводимостях определяется так:

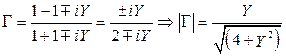. (20.18)

Резонансное окно в прямоугольном волноводе (рис. 20.5) можно рассматривать как наложение двух диафрагм – емкостной и индуктивной. Поэтому эквивалентная схема окна содержит емкостные и индуктивные элементы, включенные в ЛП параллельно. На резонансной частоте ЭМВ проходит через окно без отражений. Резонансные окна используют для разделения вакуумной и невакуумной частей СВЧ-тракта.

Резонансную l окна можно определить из формулы ( 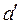и 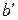– размеры отверстия):

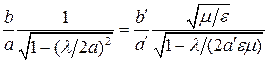. (20.19)

Индуктивный штырь (L_э) в волноводе расположен параллельно узкой стенке (рис. 20.6). ЭМВ возбуждает в штыре ток, а ток – магнитное поле, запасающее энергию.

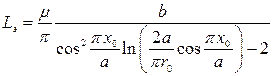. (20.20)

Список рекомендуемой литературы:[2, с. 220–226, 289–292, 324–438; 5, с. 198–210, 274–301; 6, с. 396–410; 9, с. 197–208; 11, с. 267–269, 300–310, 342–350, 379–404; 12, с. 267–276; 13, с. 293–301; 22; 37; 49].

Контрольные вопросы и задания

1. Перечислите основные виды элементов связи (возбуждения) ЛП.

2. Дайте рекомендации по размещению возбуждающего штыря в волноводе.

3. Дайте рекомендации по размещению петли связи для возбуждения линий передачи различных типов.

4. По каким принципам располагают отверстия связи в линиях передачи?

5. Опишите основные разновидности направленных ответвителей.

6. Укажите основные параметры направленных ответвителей.

7. Какие разновидности согласующих устройств вы знаете?

8. Опишите свойства волноводных тройников. Укажите область их возможного применения.

9. Почему в СВЧ устройствах и ЛП удобно использование волновых переменных (S- и Т-матриц), а не матриц сопротивлений и проводимостей?

10. Назовите основные разновидности конструктивных неоднородностей.

11. Назовите принципы управления амплитудой, фазой и поляризацией ЭМВ в линиях передачи. Приведите примеры подобных устройств управления.

12. Какие параметры имеет согласующий переход для двух линий передачи с разными волновыми сопротивлениями?

13. По какому принципу работают фильтры типов волн?

14. По какому принципу располагают возбуждающие элементы для получения нужных типов волн в ЛП и устройствах?

15. Опишите принцип действия и назначения короткозамкнутых поршней.