Основные сведения. Направляющие системы в виде линии передачи Т-волны широко применяются в радиотехнике в диапазоне от низких частот и до СВЧ

Направляющие системы в виде линии передачи Т-волны широко применяются в радиотехнике в диапазоне от низких частот и до СВЧ. Данные ЛП обладают малой дисперсией и малым затуханием в диапазонах ВЧ–УВЧ.

К двухсвязным ЛП Т-волны относятся коаксиальная, двухпроводная и различные виды полосковых линий. Для анализа распространения ЭМВ в таких ЛП применяют обобщенную модель, в которой элементарный отрезок линии заменяется эквивалентом из элементов с сосредоточенными параметрами (рис. 17.1) [2]. Данный подход основан на свойствах Т-волны при отсутствии волн высших типов и дает достаточную точность, если поперечные размеры ЛП << l, а конфигурация проводников такова, что по одному проводнику ток от генератора поступает к нагрузке, а по другому возвращается обратно к генератору.

Элементы схемы (рис. 17.1) имеют такие значения: R₀ –сопротивление проводников линии; G₀ –проводимость диэлектрика линии; L₀ и C₀ – индуктивность и емкость линии, – и называются погонными параметрами линии.

Поперечное сечение коаксиальной линии передачи (КЛ) показано на рис. 17.2 (а – радиус внутреннего проводника; b – внешнего). Внешний проводник КЛ одновременно является экраном, поэтому все ЭМП сосредоточено внутри линии в пространстве между проводниками.

Внутренний проводник имеет меньшую площадь поперечного сечения, чем внешний, и является основным источником потерь КЛ. Кроме того, пробой линии также может произойти около внутреннего проводника, так как напряженность поля в этом месте максимальна. Низшую критическую частоту из мод высших порядков имеет H₁₁ (l_кр=p(a+b)), обычно эта частота находится в СВЧ диапазоне, рабочая частота выбирается намного ниже критической, так как затухание КЛ в СВЧ диапазоне становится значительным [2].

Для повышения гибкости КЛ внутренний проводник не имеет жесткого крепления с диэлектриком, а внешний проводник выполняется в виде оплетки.

Поперечное сечение двухпроводной линии (ДЛ) показано на рис. 17.3 (а – радиус проводника, D – расстояние между осями проводников). Хотя данная линия является открытой, при выполнении условия квазистационарности считается, что все ЭМП ДЛ сконцентрировано вокруг линии внутри окружности радиусом 5D [2]. Однако на ВЧ и выше ДЛ начинает заметно излучать, так как внешние ЭМП, создаваемые противоположно направленными токами в проводах, компенсируются не полностью.

При малых расстояниях между проводниками проявляется эффект близости, который заключается в появлении асимметрии в распределении тока по сечениям проводников, что увеличивает затухание ДЛ.

При D/a > 8 эффектом близости можно пренебречь.

Проводники ДЛ одинаковы, поэтому при аналогичных с КЛ размерах затухание в проводниках линии будет меньше.

Для повышения рабочей частоты проводники ДЛ скручивают (такая ЛП называется также витой парой). Устранить излучение из ДЛ можно с помощью экранирования, но экранированная ДЛ относится к многосвязным ЛП.

При конструировании устройств УВЧ и СВЧ КЛ находят ограниченное применение как соединительные линии и линии задержки. В устройствах указанных диапазонов удобнее применять полосковые и особенно микрополосковые линии, что позволяет существенно уменьшить размеры устройств и создавать интегрированные конструкции.

На рис. 17.4 и 17.5 приведены поперечные сечения симметричной полосковой (СПЛ) и микрополосковой (МПЛ) линий соответственно.

Конструктивные параметры СПЛ:

h – толщина центрального проводника;

w – ширина центрального проводника;

b – расстояние между пластинами;

e – диэлектрическая проницаемость.

Аналогично для МПЛ:

h – толщина центрального проводника;

w – ширина центрального проводника;

b – толщина диэлектрической подложки;

e – диэлектрическая проницаемость по­д­ложки; e¢ – диэлектрическая проницаемость неограниченно простирающейся среды над подложкой и центральным проводником.

МПЛ завоевали популярность при конструировании микроэлектронных УВЧ и СВЧ устройств из-за конструктивной простоты и удобства монтажа элементов. Отсутствие симметрии и распространение ЭМВ в разных средах существенно усложняют анализ и заставляют считаться с частотной дисперсией. Для минимизации дисперсии в изготовляемом устройстве применяют заполнение диэлектриком верхнего над малым проводником пространства, что делает похожей структуру ЭМП в МПЛ на структуру ЭМП в СПЛ.

Более подробные сведения о линиях передачи Т-волны и формулы для расчета их характеристик можно найти в рекомендуемой литературе.

Телеграфные уравнения.В линиях передачи Т-волны возможен переход от векторных величин 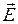и 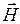к скалярным величинам U (напряжение между проводниками 1 и 2) и I (ток):

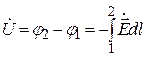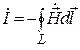; , (17.1)

где L – замкнутый контур, охватывающий проводник с током [2].

Уравнения Максвелла для линий передачи с Т-волной сводятся к известным из теории цепей телеграфным уравнениям:

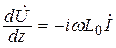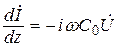; . (17.2)

Волновые уравнения для напряжения и тока.От уравнений (17.2) можно перейти к волновым уравнениям для напряжения и тока:

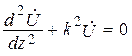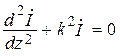; , (17.3)

где волновое число при отсутствии потерь .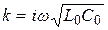

Характеристическое сопротивление ЛП с малыми потерями

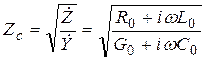. (17.4)

Для учета потерь в диэлектриках и проводниках линии передачи в уравнение (17.2) вводят комплексные сопротивление и проводимость

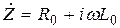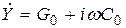; . (17.5)

В этом случае (17.2) запишется в виде

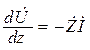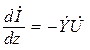; , (17.6)

а волновое число 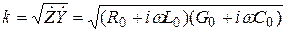[2].

Характеристическое сопротивление линии передачи с учетом потерь (17.5) определяется формулой

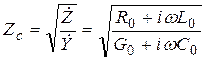. (17.7)

В линии без потерь (R₀ = 0, G₀ = 0)

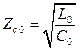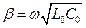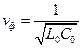; ; . (17.8)

Решением волновых уравнений (17.3) для напряжения и тока являются соответственно прямые и обратные волны напряжения и тока, аналогичные (7.8):

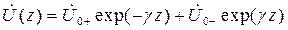; (17.9)

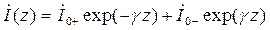. (17.10)

Для линий передачи Т-волны можно связать L₀, С₀ и Z_c0 так :

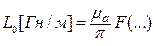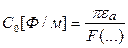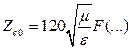, , , (17.11)

где F(…) – функция, связанная с геометрическими размерами линии.

Характеристики КЛ определяются по формулам [2]:

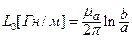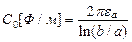; ; (17.12)

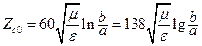; (17.13)

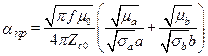; (17.14)

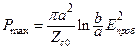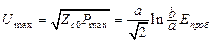; , (17.15)

где E_проб – пробивная напряженность диэлектрика КЛ; U_max – максимально допустимое напряжение в КЛ; P_max – предельно допустимая мощность в КЛ.

Анализ (17.12)–(17.15) позволил найти соотношения конструктивных параметров для достижения оптимальных характеристик [2].

Минимум затуханиядостигается при b/a = 3,6…5,6, Z_c0 = (77…103)/ 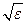,что соответствует стандартному значению Z_c0 = 75 Ом.

Максимум напряжения пробоя КЛ достигается при b/a = 2,72, Zc0 = 60/ 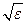, что соответствует стандартному значению Z_c0 = 50 Ом.

Максимум передаваемой мощности достигается при b/a=1,65, Z_c0 = 30/ 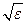, что соответствует Z_c0 = 30 Ом. В данное время КЛ с Z_c0 = 30 Ом применяется достаточно редко.

КЛ с Z_c0 = 75 Ом применяется в приемной технике УКВ диапазона (соединение приемника телевещания или радиовещания с антенной), а с Z_c0 = 50 Ом – в связной технике (передача, прием-передача).

Характеристики ДЛ (m₁ – m диэлектрика, а m₂ – m проводников):

;

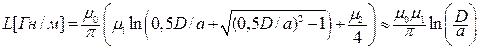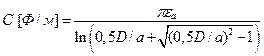
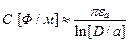. (17.16)

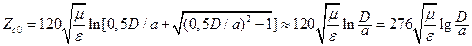. (17.17)

Приближенные формулы можно использовать при значительном расстоянии между проводниками ДЛ (D/a > 6).

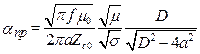; (17.18)

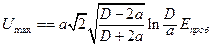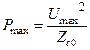; . (17.19)

Точные методы расчета характеристик СПЛ и МПЛ содержат сложные и неявно заданные формулы, аппроксимация которых привела к существованию разнообразных формул разной степени точности. Для оценочных расчетов характеристик СПЛ и МПЛ рекомендуется применять простейшие формулы [2, 22а, 23].

Характеристики СПЛ определяются формулами

при w/(b–h) < 1 ;

при w/(b–h) > 1 ; (17.20)

;

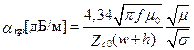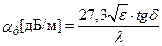. (17.21)

На рис. 17.6 приведен график зависимости Z_cСПЛ от w/b приh/b = 0,01 и e = 1, построенный по формулам (17.20). Сравнение с точными значениями [25] показывает, что погрешность (17.20) в данном случае не превышает ± 5 % [22а].

Характеристики МПЛ определяются формулами

при w/b < 2;

при w/b ³ 2; (17.22)

; ;

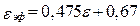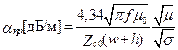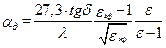. (17.23)

На рис. 17.7 приведены графики зависимости Z_cМПЛ от w/b приh/b = 0,01 и e = 3,8, построенные по формулам (17.22) и точным значениям из [25]. Анализ показывает, что погрешность (17.22) в данном случае не превышает 20 % [23].

Оценка дисперсии в ЛП Т-волны проводится в предположении малости потерь, что позволяет разделить потери в проводнике и потери в диэлектрике. Появление потерь вызывает появление продольных составляющих ЭМВ, но при малых потерях отличие ЭМП от ЭМП Т-волны пренебрежимо мало [2, 50].

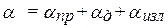, (17.24)

где 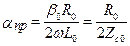; ; 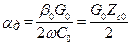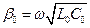, в закрытых ЛП a_изл = 0.

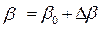, (17.25)

где 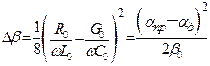– дисперсионная добавка коэффициента фазы.

Кроме изменения a и b, групповой и фазовой скоростей, потери вызывают частотную зависимость характеристического сопротивления

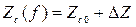, (17.26)

где 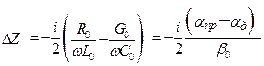– дисперсионная добавка [2].

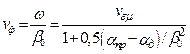. (17.27)

Активная проводимость утечки в изоляции G₀ определяется так [2]:

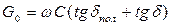. (17.28)

Из (10.15) с помощью формулы (10.12) находим составляющую коэффициента затухания, определяемую потерями в диэлектрике:

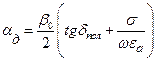. (17.29)

Полученное равенство справедливо для любого типа линий. Для любых технических диэлектриков на ВЧ и выше можно пренебречь вторым слагаемым в скобках по сравнению с первым. Величина 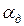растет пропорционально частоте.

Скин-эффект в проводниках приводит к появлению реактивной составляющей, что требует замены R₀ на Z₀ = R₀ +iX₀ . На ВЧ и выше Z₀ (f) определяется так:

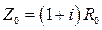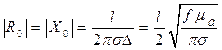, . (17.30)

В линиях с малыми потерями отличие v_ф от v_em и Z_c от Z_c0 мало.

Из (17.25) – (17.27) видно, что при выполнении условия 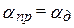дисперсионные искажения отсутствуют, и условие неискаженной передачи через первичные параметры записывается так:

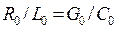. (17.31)

В прошлом, когда сообщения по линиям связи передавались на дальние расстояния на НЧ, особое значение придавали выполнению условия (17.31), для чего искусственно увеличивали индуктивность ЛП. В настоящее время это не требуется, так как потери в диэлектриках ЛП малы.

Условие неискаженной передачи с учетом (17.29) – (17.31) выполняется на некоторой частоте ОВЧ-СВЧ диапазонов, которая зависит от параметров линии. На рис. 17.8 приведены частотные зависимости составляющих затухания.

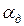~f ; 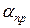постоянно на низких частотах, а на более высоких ~f ^0,5. Следовательно, на НЧ 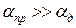, 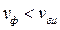и растет с частотой. Потери в проводниках линии вызывают ано­маль­ную дисперсию ЭМВ.

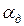растет с частотой быстрее, чем 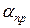, и некоторой частоте f_нп в диапазоне ОВЧ-СВЧ достигается условие неискаженной передачи. 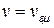; 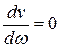, групповая скорость постоянна, и дисперсионных искажений нет.

При f > f_нп 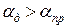, наблюдается нормальная дисперсия. Из-за большой величины b изменение v(f) и других параметров настолько невелико, что дисперсией пренебрегают [2].

Таким образом, дисперсию ЭМВ в линиях передачи Т-волны и комплексный характер Z_c обычно учитывают только на НЧ.

В диапазонах УВЧ и СВЧ при анализе распространения относительно узкополосных сигналов влиянием дисперсии можно пренебречь.

Наибольшую дисперсию имеют МПЛ [23, 48]:

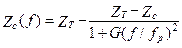, (17.32)

где 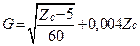, , 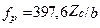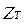– Z_c СПЛ шириной w и высотой 2b.

Однако в любой октаве рассматриваемых диапазонов относительные изменения вторичных параметров МПЛ не превышают 1%.

Список рекомендуемой литературы:[2, с. 229–254; 3, гл. 16, с. 85–86; 5, с. 102–120; 6, с. 203–205, 257–263, 276–281; 7, с. 170–175; 9, с. 239–251, 289–293; 10, с. 239–251, 289–293; 11, с. 219–220, 262–267, 269–275; 12, с. 224–229; 13, с. 279–284, 309–310; 14; 17–28, 48, 50].

Контрольные вопросы и задания

1. Опишите конструкции основных линий передачи Т-волны.

2. Запишите формулы для вычисления волнового сопротивления линий передачи Т-волны основных типов.

3. Опишите распределение ЭМП в пространстве линий передачи Т-волны.

4. Поясните физический смысл понятий тока и напряжения в линиях передачи Т-волны.

5. Дайте сравнительную характеристику параметров коаксиальной и двухпроводной линий.

6. Какие достоинства имеет двухпроводная линия в виде «витой пары»?

7. Назовите основные разновидности полосковых линий.

8. Дайте сравнительную характеристику СПЛ и МПЛ.

9. Какие особенности имеют многосвязные линии?

10. Какое влияние оказывает синфазность или противофазность возбуждения проводников связанных линий?

11. Укажите основные разновидности и область применения многосвязных ЛП.

12. Чем отличается Т-волна от квази-Т-волны?

13. По каким критериям выбирают Z_c коаксиальных линий?

14. Для каких радиотехнических целей используются коаксиальные кабели с характеристическим сопротивлением 50 и 75 Ом?