Диэлектрики с малыми потерями

Если ток проводимости будет мал по сравнению с током смещения, мал будет и угол диэлектрических потерь δ. В этом случае формулы для расчета характеристик волны можно упростить. При уменьшении аргумента косинус стремится к единице, а синус и тангенс – к величине угла, выраженной в радианах. С учетом этого из формул (5.7), (5.9), (5.10) и (5.15) получим:

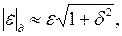
	(5.18)
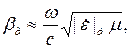
	(5.19)
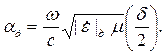
	(5.20)
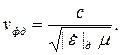
	(5.21)

Здесь и далее нижним индексом «д» отмечена принадлежность параметра диэлектрику с малыми потерями

Формула для волнового сопротивления останется прежней, за исключением обозначения принадлежности модуля комплексной относительной диэлектрической проницаемости к диэлектрику с малыми потерями.

Вычислим относительную погрешность расчета характеристик электромагнитного поля по приближенным формулам. Она описывается следующим соотношением:

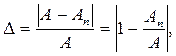
(5.22)

где	А	- величина, рассчитанная по точной формуле;
	А_п	- величина, рассчитанная по приближенной формуле.

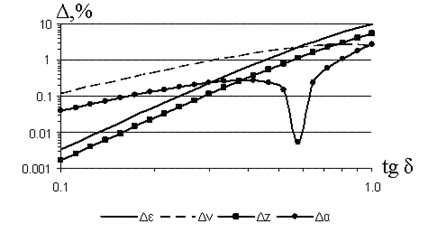
Подставив в эту формулу выражения для соответствующих характеристик электромагнитного поля, легко получить формулы для вычисления относительных погрешностей. Зависимость относительных погрешностей перечисленных характеристик волны от тангенса угла диэлектрических потерь приведены на рис. 5.1 и в таблице 5.1.

Эти данные позволяют оценить возможность применения приближенных формул при заданной погрешности вычисления. Например, если фазовая скорость должна быть рассчитана с погрешностью не более 0,5 %, приближенные формулы нельзя применять при tg δ > 0.19.

Интерес представляет зависимость относительной погрешности коэффициента затухания потому, что она имеет минимум. Это значит, что имеется величина tg δ, при которой погрешность равна нулю.

Рис. 5.1. Графики зависимости относительных погрешностей расчетов по приближенным формулам от tg δ

Таблица 5.1.

Относительная погрешность расчетов по приближенным формулам

tg δ	Δ_ε, %	Δ_v, %	Δ_z, %	Δ_α, %	tg δ	Δ_ε, %	Δ_v, %	Δ_z, %	Δ_α, %
0.10	0.00	0.12	0.00	0.04	0.33	0.35	1.13	0.17	0.26
0.11	0.01	0.15	0.00	0.05	0.37	0.51	1.34	0.26	0.27
0.12	0.01	0.19	0.00	0.06	0.42	0.76	1.57	0.38	0.27
0.14	0.01	0.23	0.01	0.07	0.46	1.11	1.81	0.56	0.23
0.16	0.02	0.29	0.01	0.09	0.52	1.59	2.07	0.81	0.15
0.17	0.03	0.35	0.01	0.11	0.58	2.26	2.31	1.15	0.01
0.19	0.04	0.43	0.02	0.13	0.65	3.17	2.53	1.62	0.23
0.22	0.07	0.53	0.03	0.15	0.72	4.36	2.69	2.25	0.60
0.24	0.10	0.65	0.05	0.18	0.80	5.89	2.78	3.08	1.11
0.27	0.15	0.78	0.08	0.21	0.90	7.81	2.75	4.15	1.81
0.30	0.23	0.94	0.12	0.24	1.00	10.14	2.56	5.49	2.72

Задачу нахождения величины tg δ, при которой погрешность равна нулю, можно решить графически или численно. Численное решение дает Δ_α = 6.99*10^-11% при tg δ = 0.580696. При этом значении тангенса угла электрических потерь погрешности вычисления коэффициента затухания практически не будет. Правда, погрешности расчета остальных параметров волны будут достаточно велики, 1 – 2%.

<16 17 181920 21 22 >

Дата добавления: 2015-06-12; просмотров: 1106;