Проводники

К проводникам относятся среды, в которых токи проводимости много больше токов смещения. В первую очередь это металлы. Для большинства металлов не существует радиочастот, на которых токи смещения хотя бы сравнялись с токами проводимости.

Из формулы для tg δ видно, что при прочих равных условиях, чем ниже частота, тем среда с электропроводностью ближе к идеальному проводнику. На достаточно низких радиочастотах многие, на первый взгляд диэлектрические среды становятся металлоподобными. Так, например, ведет себя сухая почва на частотах в несколько МГц. Это свойство в ряде случаев значительно упрощает решение практических задач.

В хороших проводниках токи смещения пренебрежимо малы. Согласно этому допущению комплексную диэлектрическую проницаемость металлоподобной среды можно считать чисто мнимой:

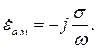
(5.23)

Нижним индексом «м» отмечена принадлежность параметра проводнику.

Найдем комплексное волновое число плоских электромагнитных волн в такой среде. По общему правилу действий с комплексными числами для него можно записать следующее соотношение:

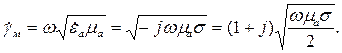
(5.24)

При извлечении корня квадратного из –j использована следующая формула:

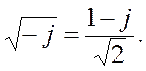
(5.25)

Из формулы (5.24) легко получить выражения для коэффициента фазы, коэффициента затухания и фазовой скорости электромагнитной волны в проводнике:

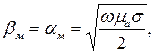
	(5.26)
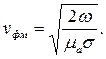
	(5.27)

Отличительной особенностью фазовой скорости электромагнитных волн в проводнике является ее зависимость от частоты. Значит, в проводниках имеет место быть частотная дисперсия фазовой скорости. Кроме того, скорость электромагнитных волн в проводниках невелика.

Фазовая скорость электромагнитных волн в проводнике значительно меньше скорости света в вакууме

Для определения волнового сопротивления металла обратимся к формуле (4.12) и подставим в нее выражение для комплексной абсолютной диэлектрической проницаемости (5.23). Получим:

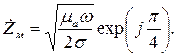
(5.28)

Формула (5.28) весьма показательна: волновое сопротивление металла весьма мало.