Полупроводники
Наиболее общим случаем среды распространения электромагнитных волн являются диэлектрики с потерями или полупроводники. Тангенс угла диэлектрических потерь полупроводников не так мал, чтобы отнести их к диэлектрикам, и не так велик, чтобы отнести к проводникам.
Для анализа распространения электромагнитных волн в диэлектрике с потерями воспользуемся комплексной абсолютной диэлектрической проницаемостью:
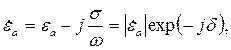
| (5.3) |
| где | 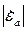
| - модуль комплексной абсолютной диэлектрической проницаемости, Ф/м; |
| δ | - угол диэлектрических потерь, ˚ или рад: |
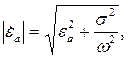
| (5.4) |
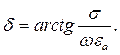
| (5.5) |
Формулу (5.4) целесообразно преобразовать. Дело в том, что в начале расчетов для определения класса, к которому принадлежит среда, надо вычислить tg δ. Если среду удастся отнести к проводникам или диэлектрикам, можно будет воспользоваться упрощенными формулами. Поэтому целесообразно использовать результаты этих расчетов. Вынесем абсолютную диэлектрическую проницаемость из-под корня. Получим:
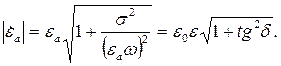
| (5.6) |
По аналогии с действительной относительной диэлектрической проницаемостью вводится комплексная относительная диэлектрическая проницаемость. Она определяется как отношение комплексной абсолютной диэлектрической проницаемости к электрической постоянной. Аргумент комплексной относительной диэлектрической проницаемости останется таким же, как и у абсолютной диэлектрической проницаемости, а модуль описывается формулой:
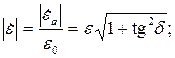
| (5.7) |
Аналогично можно ввести и магнитные потери. Но на практике подавляющее большинство сред, в которых распространяются электромагнитные волны, не имеют магнитных потерь. Значит, их можно не учитывать, и формула для комплексного волнового числа диэлектрика с электрическими потерями примет вид:
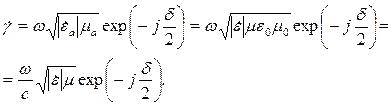
| (5.8) |
Для описания коэффициента фазы и коэффициента затухания надо раскрыть выражение (5.8) по формуле Эйлера. Получим:
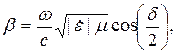
| (5.9) |
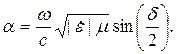
| (5.10) |
Коэффициент фазы – это скорость изменения фазы волны с расстоянием. Он показывает, на сколько радиан изменится фаза волны при прохождении пути в 1 метр. Произведение βz показывает, на сколько радиан изменится фаза волны при прохождении пути z.
Описание затухания волны сложнее. Пусть в точке z1 амплитуда вектора напряженности электрического поля равна Е1. Рассчитаем напряженность поля Е2 в точке z2. Процесс изменения амплитуды вектора напряженности электрического поля на пути между точками z1 и z2 описывается показательной функцией:
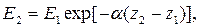
| (5.11) |
| где | E1 | - модуль вектора напряженности электрического поля в начале пути, при z = z1, В/м; |
| E2 | - модуль вектора напряженности электрического поля в конце пути, при z = z2, В/м; | |
| α | - коэффициент затухания, 1/м; |
Уменьшение амплитуды волны называется затуханием и рассчитывается как отношение E1 к E2:
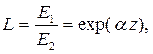
| (5.12) |
| где | L | - затухание; |
| z | - расстояние между точками z1 и z2, м. |
Затухание показывает, во сколько раз уменьшилась амплитуда волны на пути z. Обычно его логарифмируют. Если вычисляется натуральный логарифм, затухание получается в неперах:
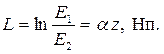
| (5.13) |
Однако чаще для описания затухания используют децибелы. Тогда формула имеет вид:
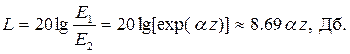
| (5.14) |
Для расчета фазовой скорости надо воспользоваться общей формулой (1.7). После подстановки в нее выражения (5.9) для коэффициента фазы получим:
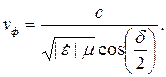
| (5.15) |
Эта формула хорошо отражает физическую суть изменений фазовой скорости электромагнитных волн при изменении параметров среды.
Дата добавления: 2015-06-12; просмотров: 1364;
