Количество тепла, необходимое для превращения единицы массы вещества в жидкость при температуре плавления, называют удельной теплотой плавления L.

Для плавления вещества массой m необходимо затратить количество теплоты равное:

Q = L·m. (5.8)

При охлаждении расплавленного твёрдого тела происходит обратный процесс, называемый кристаллизацией. Образование кристалла также происходит при постоянной температуре, равной температуре плавления. При кристаллизации жидкости выделяется такое же количество теплоты, какое поглощается при плавлении вещества той же массы.

Аморфные тела в противоположность кристаллам не имеют определенной температуры плавления.

5.6. Критическое состояние

На рисунке 5.3 дано семейство изотерм реального газа. Видно, что с повышением температуры горизонтальные участки изотерм сокращаются, стягиваясь в точку при температуре называемой критической. В критической точке исчезает всякое различие между жидкостью и паром. Это состояние называют критическим состоянием вещества. Объём V_кр, давление p_кр, и температура Т_кр, отвечающие критическому состоянию, называются критическими величинами. Для критической изотермы точка К служит точкой перегиба, а касательная в ней параллельна оси V.

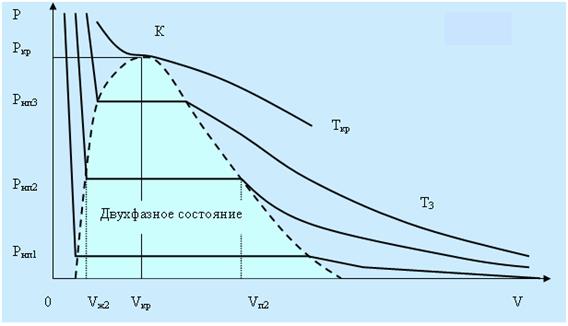
Рис. 5.3.

При температурах выше критической понятие насыщенного пара теряет смысл. Колоколообразная кривая ограничивает область двухфазных состояний. При температурах выше критической вещество при любых давлениях будет однородным и никаким сжатием не может быть осуществлено ожижение вещества. В области левее колоколообразной кривой находится жидкое состояние, а правее пар.

Выбрав процесс перехода так, что бы он не пересекал двухфазную область, можно осуществить переход из жидкого в газообразное состояние без расслаивания на две фазы. При этом вещество всё время будет оставаться однородным.

5.6. Пересыщенный пар и перегретая жидкость. Метастабильное состояние вещества.

На рисунке 5.4 изображены изотермы Ван дер Ваальсовского газа. Характерным для них является то, что при температурах, ниже критической, у кривых имеется S-образный завиток. У реальных изотерм его нет, а на его месте находится прямолинейный горизонтальный участок.

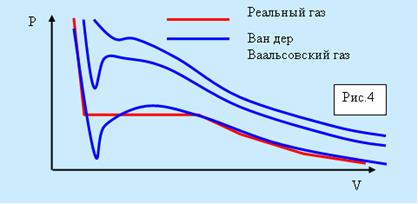
Рис. 5.4. Изотермы для газа Вад-дер-Ваальса.

Из рисунка видно, что уравнение Ван дер Ваальса хорошо описывает газообразное и жидкое состояние. На участке 1-4 рисунка 5.5 вещество ведёт себя совершенно необычно.

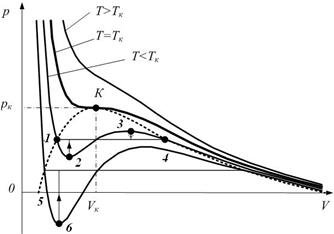
Рис. 5.5. Метастабильные состояния.

Тем не менее, участок 1-2 может быть реализован. Точки на участке 1-2 соответствуют состояниям перегретой жидкости. Точки на участке 4-3 пересыщенному пару.Эти состояния являются неустойчивыми и стрелочки на рисунке показывают направление возможного перехода – при этом происходит расслоение на две фазы. Такие состояния называются метастабильными.При достаточно низких температурах изотерма пересекает ось V_m, переходя в область отрицательных давлений (рис. 5.5, нижняя кривая). Вещество под отрицательным давлением находится в состоянии растяжения. При некоторых условиях такие состояния также реализуются. Участок 5–6 на нижней изотерме растянутой жидкости.

Что бы получить метастабильное состояние необходимо очистить вещество от всевозможных пылинок, микрочастиц и всего, что может стать центром конденсации или центром кипения. Тогда, например, жидкость можно перевести в метастабильное состояние перегретой жидкости. Однако, достаточно бросить в перегретую жидкость песчинку, как произойдёт бурное закипание, температура жидкости станет равной температуре кипения, а избыток тепла будет истрачен на парообразование. На участке 2-3 рис. 5.5. вещество обладало бы противоестественными свойствами, так как при увеличении объёма давление бы повышалось. Поэтому такие состояния не реализуются.

5.8. Уравнение Клапейрона –Клаузиуса

Рассмотрим элементарный цикл Карно в области фазового перехода (рис. 5.7).

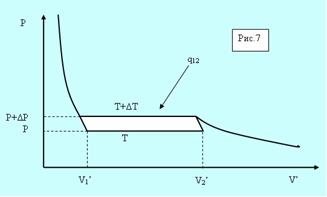
Рис. 5.7. Фазовый переход.

Горизонтальные участки соответствуют изотермам в процессе фазового перехода отличающимся на ΔТ, а вертикальные – адиабатам (они круче изотерм). По определению кпд цикла равно

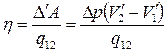. (5.8)

Здесь V’₁ и V’₂ – удельные объёмы фаз, а q₁₂- удельная теплота сообщаемая единице массы системы при расширении.

Но кпд цикла Карно можно также записать через температуры нагревателя и холодильника:

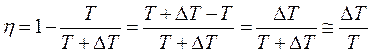. (5.9)

Приравняем (5.8) и (5.9)

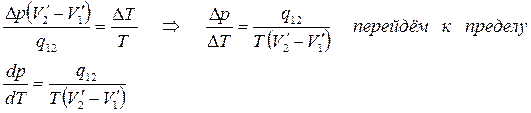(5.10)

Это уравнение называется уравнением Клапейрона – Клаузиуса.

Согласно уравнению (5.10) знак производной зависит от того, каким изменением объёма – возрастанием или уменьшением - сопровождается фазовый переход, происходящий при поглощении тепла. При испарении жидкости или твёрдого тела объём всегда увеличивается, поэтому производная dp/dT >0 для кривой сублимации и испарения. При плавлении объём обычно возрастает, однако, у некоторых веществ, в том числе у воды, объём твёрдой фазы больше объёма жидкой. В этом случае dp/dT <0.

5.9. Диаграмма состояния. Тройная точка.

Возьмём вещество в виде жидкости и находящегося в равновесии с ней пара и, не изменяя объема, начнём отнимать тепло. Понижение температуры будет сопровождаться понижением давления. Это будет продолжаться до тех пор, пока не будет достигнута температура кристаллизации. Обозначим её Т_тр.

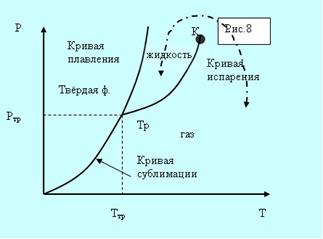
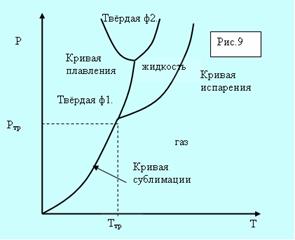
а б

Рис. 5.8. Фазовые диаграммы.

Всё время пока идёт кристаллизация, температура и давление остаются неизменными. Отводимое тепло представляет собой тепло, выделяемое при кристаллизации. Температура Т_тр и давление р_тр– единственные значения, при которых могут одновременно находится в равновесии три фазы вещества: твёрдая, жидкая, газообразная. Соответствующая точка на диаграмме (р,Т) называется тройной точкой.

Кривые плавления, испарения и сублимации разбивают координатную плоскость на три области (рис. 5.8, а). Любая точка в одной из областей соответствует однофазному состоянию вещества. Точки, лежащие на кривых, соответствуют равновесным двухфазным состояниям вещества. Кривая испарения заканчивается критической точкой К. Можно осуществить процесс в обход её, так что переход от газа к жидкости не будет проходить через двухфазное состояние (пунктирная кривая на рис. 5.8, а).

Для вещества с несколькими кристаллическими модификациями может быть несколько тройных точек. Например, для двух модификаций на рисунке 5.8, б присутствуют две тройные точки. Непрерывный переход между жидким и газообразным состоянием возможен потому, что различие между ними носит количественный характер. Непрерывный переход между жидким и кристаллическим состоянием не возможен потому, что характерной чертой является анизотропия – наличие кристаллической решётки. У жидкости анизотропия отсутствует, а переход между анизотропным и не анизотропным состояниями может происходить только скачком. По этой причине кривые сублимации и плавления не могут обрываться критической точкой.