Дисперсия оптической активности.
Существенно большую информацию, чем измерение угла j на одной длине волны несут исследования дисперсии оптической активности, т.е. зависимости j от l.
Рассмотрим простейшую модель, показывающую оптическую активность, а именно, так называемую модель Куна. Она представляет собой среду, заполненную несимметрично расположенными парами осцилляторов, взаимодействующих друг с другом. Тогда плоскость поляризации света, проходящего через такую среду, будет поворачиваться на угол j, причем
 (6.3)
(6.3)
В этой формуле w – круговая частота падающего на молекулу света, w1, w2 – частоты колебаний 1‑го и 2‑го осциллятора ( 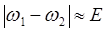 (эн-я вз-я)), f0 – сила невзаимодействующего осциллятора, n – количество осцилляторов в единице объема. В этой формуле не учтено затухание колебаний осцилляторов, поэтому она справедлива в области частот, в которой w ¹ w1, w2, т.е. в области, далекой от области собственных частот осцилляторов. Дисперсия величин j и q в модели Куна представлена на рис. 17.
(эн-я вз-я)), f0 – сила невзаимодействующего осциллятора, n – количество осцилляторов в единице объема. В этой формуле не учтено затухание колебаний осцилляторов, поэтому она справедлива в области частот, в которой w ¹ w1, w2, т.е. в области, далекой от области собственных частот осцилляторов. Дисперсия величин j и q в модели Куна представлена на рис. 17.
Строгая квантовомеханическая теория дает следующее выражение для угла j поворота плоскости поляризации света:
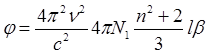 (6.4)
(6.4)
В этой формуле n – частота света, N1 – число молекул в единице объема (1 см3), n – показатель преломления раствора, b – молекулярный параметр, выражающийся через квантовомеханические характеристики молекулы.
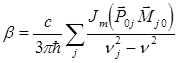 (6.5)
(6.5)
Здесь 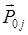 – электрический дипольный момент перехода между состояниями 0 и j (
– электрический дипольный момент перехода между состояниями 0 и j (  ),
),  – магнитный дипольный момент перехода (
– магнитный дипольный момент перехода ( 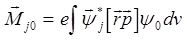 ). Величина в числителе под знаком суммы называется силой вращения Rj.
). Величина в числителе под знаком суммы называется силой вращения Rj.
Чтобы проводить вычисления по этой формуле, необходимо знать полный набор волновых функций и энергетических уровней молекулы. Эта формула похожа на формулу для поляризуемости a, известную из квантовой механики:
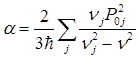 (6.6)
(6.6)
В случае нескольких собственных частот осцилляторов ωi формула для угла поворота плоскости поляризации в терминах длин волн принимает вид (см. 6.3 и 6.5):
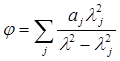 (6.7)
(6.7)
где величины aj выражаются через λj, Rj и физические постоянные. Эта формула описывает различные биологические объекты, вращающие плоскость поляризации света.
Так, дисперсия оптической активности полиаминокислоты в виде статического клубка описывается одночленной формулой:
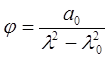 (6.8)
(6.8)
Величина a0=268 нм. Напомним, что формулы (6.5), (6.7) справедливы в области, далекой от собственного поглощения, т.е. в области нормальной дисперсии.
Для π → π* переходов в a‑спирали белка опытные данные по дисперсии оптического вращения в области нормальной дисперсии удовлетворительно описываются формулой вида (6.7), состоящей из двух членов:
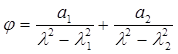 (6.9)
(6.9)
Эту формулу можно преобразовать к новым параметрам
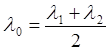 ;
; 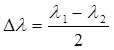
При этом она приобретает следующий вид (с точностью до (????????)):
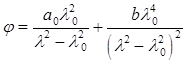 (6.10)
(6.10)
где
 ;
;  (6.11)
(6.11)
Большой интерес для приложений представляет параметр b~Dl разности длин волн взаимодействующих осцилляторов. Эта величина пропорциональна энергии взаимодействия между осцилляторами, т.е. степени a‑спиральности (относительному содержанию a-спиральных участков в молекуле белка). Параметры a0 и b определяются с помощью следующего приема. По известной экспериментальной зависимости φ(λ) строят новую функцию 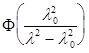 , которая определяется следующим образом:
, которая определяется следующим образом:
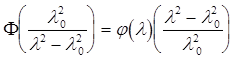
Как видно из формулы (6.10) функция F будет иметь вид:
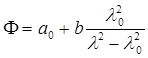 (6.11а)
(6.11а)
 |
Таким образом
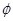 является линейной функцией
является линейной функцией 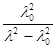 . Если мы сможем достроить функцию
. Если мы сможем достроить функцию  как функцию
как функцию 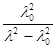 мы легко графически определим величины а0 и b=tg
мы легко графически определим величины а0 и b=tg 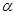 (рис.18).
(рис.18).
Рис. 18
Напомним, что в этом случае величина b пропорциональна содержанию  -спиральных областей белка. Более подробно степень спиральности определяется так. Для белка со спирализованными и неспирализованными участками величина вращения складывается из выражений (6.8) и (6.9):
-спиральных областей белка. Более подробно степень спиральности определяется так. Для белка со спирализованными и неспирализованными участками величина вращения складывается из выражений (6.8) и (6.9):
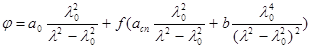 (6.12)
(6.12)
В координатах, показанных на рис.18 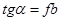 , а отрезок, отсекаемый по вертикальной оси, равен
, а отрезок, отсекаемый по вертикальной оси, равен 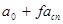 . Величины
. Величины 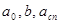 находятся из экспериментальных данных по дисперсии оптической активности денатурированных и нативных
находятся из экспериментальных данных по дисперсии оптической активности денатурированных и нативных 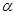 -спиральных аминокислот. Обычно используются следующие величины упомянутых параметров:
-спиральных аминокислот. Обычно используются следующие величины упомянутых параметров: 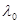 =212 нм,
=212 нм, 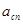 =650,
=650, 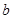 = -630 град. см2 децимоль-1. Если
= -630 град. см2 децимоль-1. Если 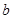
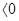 , то так вращает плоскость поляризации правая спираль, если
, то так вращает плоскость поляризации правая спираль, если 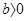 , мы имеем дело с левой
, мы имеем дело с левой 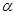 -спиралью.
-спиралью.
Дата добавления: 2015-06-10; просмотров: 912;
