Допуски формы.

В основу формирования и количественной оценки отклонений формы поверхностей положен принцип прилегающих элементов.

Прилегающий элемент, это элемент соприкасающийся с реальной поверхностью и расположенный вне материала детали, так чтобы расстояние от него в наиболее удалённой точке реальной поверхности в пределах нормируемого участка имело бы минимальное значение.

Прилегающим элементом может быть: прямая, плоскость, окружность, цилиндр и т.п. (Рис. 1, 2).

1 - прилегающий элемент;

2 – реальная поверхность;

L - длина нормируемого участка;

Δ - отклонение формы, определяемое от прилегающего элемента по нормали к поверхности.

Т - допуск формы.

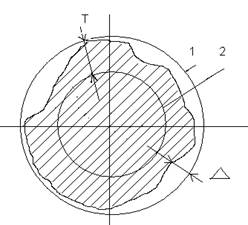
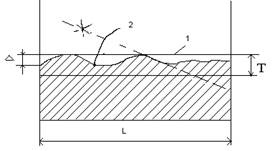
Рис 2. Рис. 1

Поле допуска - область в пространстве, ограниченная двумя эквидистантными поверхностями, отстоящими одна от другой на расстоянии равном допуску Т, который откладывается от прилегающего элемента в тело детали.

Количественное отклонение формы оценивают наибольшим расстоянием 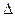от точек реальной поверхности (профиля) до прилегающей поверхности (профиля) по нормали к последней (рис.2). Прилегающими поверхностями служат: рабочие поверхности рабочих плит, интерференционных стекол, лекальных линеек, калибров, контрольных оправок и т.п.

Допуском формы называется наибольшее допускаемое отклонение Δ (рис.2).

Отклонения формы поверхностей.

1. Отклонение от прямолинейности в плоскости – это наибольшее 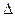от точек реального профиля до прилегающей прямой. (Рис. 3а).

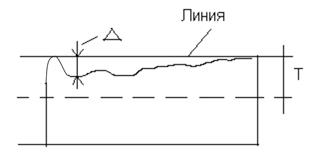
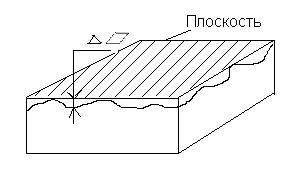
Рис. 3

а) б)

Обозначение на чертеже:

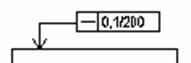
Допуск прямолинейности 0,1мм на базовой длине 200мм

2. Допуск плоскостности 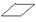- это наибольшее допускаемое расстояние ( ) от точек реальной поверхности до прилегающей плоскости в пределах нормированного участка (Рис. 3б).

Обозначение на чертеже:

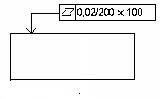
Допуск плоскостности (не более) 0,02мм на базовой поверхности 200 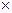100 мм.