Принципы помехоустойчивого кодирования
В теории помехоустойчивого кодирования важным является вопрос об использовании избыточности для корректирования возникающих при передаче ошибок. Здесь удобно рассмотреть блочные коды, в которых всегда имеется возможность выделить отдельные кодовые комбинации. Для равномерных кодов, число возможных комбинаций равно М=2n, где п — значность кода.
В обычном некорректирующем коде без избыточности, например, в коде Бодо, число комбинаций М выбирается равным числу сообщений алфавита источника М0, и все комбинации используются для передачи информации. Корректирующие коды строятся так, чтобы число комбинаций М превышало число комбинаций источника М0. Однако в этом случае лишь М0 комбинаций из общего числа используются для передачи информации. Эти комбинации называются разрешенными, а остальные М — М0 комбинации носят название запрещенных. На приемном конце в декодирующем устройстве известно, какие комбинации являются разрешенными и какие — запрещенными. Поэтому если переданная разрешенная комбинация в результате ошибки преобразуется в некоторую запрещенную комбинацию, то такая ошибка будет обнаружена, а при определенных условиях — исправлена. Естественно, что ошибки, приводящие к образованию другой разрешенной комбинации, не обнаруживаются.
Различие между комбинациями равномерного кода принято характеризовать расстоянием, равным числу символов, которыми отличаются комбинации одна от другой. Расстояние dij между двумя комбинациями Ai и Aj определяется количеством единиц в сумме этих комбинаций по модулю два. Например:
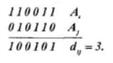
Для любого кода 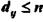 . Минимальное различие между разрешенными комбинациями в данном коде называется кодовым расстоянием
. Минимальное различие между разрешенными комбинациями в данном коде называется кодовым расстоянием 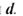
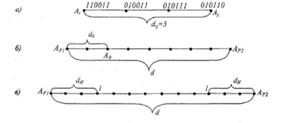
Рис. 11.1. Геометрическое представление разрешенных и запрещенных кодовых комбинаций
Расстояние между комбинациями 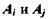 условно обозначено на рис.11.1а, где показаны промежуточные комбинации, отличающиеся друг от друга одним символом. В общем случае некоторая пара разрешенных комбинаций.
условно обозначено на рис.11.1а, где показаны промежуточные комбинации, отличающиеся друг от друга одним символом. В общем случае некоторая пара разрешенных комбинаций.  и
и 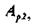 разделенных кодовым расстоянием
разделенных кодовым расстоянием 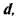 изображается на прямой рис. 11.1б, где точками указаны запрещенные комбинации. Для того чтобы в результате ошибки комбинации
изображается на прямой рис. 11.1б, где точками указаны запрещенные комбинации. Для того чтобы в результате ошибки комбинации  преобразовалась в другую разрешенную комбинацию
преобразовалась в другую разрешенную комбинацию 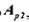 , должно исказиться d символов. При искажении меньшего числа символов комбинация
, должно исказиться d символов. При искажении меньшего числа символов комбинация 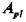 перейдет в запрещенную комбинацию, и ошибка будет обнаружена. Отсюда следует, что ошибка всегда обнаруживается, если ее кратность, т. е. число искаженных символов в кодовой комбинации:
перейдет в запрещенную комбинацию, и ошибка будет обнаружена. Отсюда следует, что ошибка всегда обнаруживается, если ее кратность, т. е. число искаженных символов в кодовой комбинации:
 (11.2)
(11.2)
Если g <d , то некоторые ошибки также обнаруживаются. Однако полной гарантии обнаружения ошибок здесь нет, так как ошибочная комбинация в этом случае может совпасть с какой-либо разрешенной комбинацией. Минимальное кодовое расстояние, при котором обнаруживаются любые одиночные ошибки, d = 2.
Процедура исправления ошибок в процессе декодирования сводится к определению переданной комбинации по известной принятой. Расстояние между переданной разрешенной комбинацией и принятой запрещенной комбинацией d0 равно кратности ошибок g. Если ошибки в символах комбинации происходят независимо относительно друг друга, то вероятность искажения некоторых g -символов в п -значной комбинации будет равна:
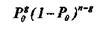 (11.3)
(11.3)
где Р0 — вероятность искажения одного символа. Так как обычно 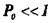 то вероятность многократных ошибок уменьшается с увеличением их кратности, при этом более вероятны меньшие расстояния
то вероятность многократных ошибок уменьшается с увеличением их кратности, при этом более вероятны меньшие расстояния 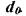 В этих условиях исправление ошибок может производиться по следующему правилу. Если принята запрещенная комбинация, то считается переданной ближайшая разрешенная комбинация Например, пусть образовалась запрещенная комбинация А0 (см. рис. 11.2б), тогда принимается решение, что была принята комбинация А1. Это правило декодирования для указанного распределения ошибок является оптимальным, так как оно обеспечивает исправление максимального количества ошибок. (В общем случае оптимальное правило декодирования зависит от распределения ошибок.)
В этих условиях исправление ошибок может производиться по следующему правилу. Если принята запрещенная комбинация, то считается переданной ближайшая разрешенная комбинация Например, пусть образовалась запрещенная комбинация А0 (см. рис. 11.2б), тогда принимается решение, что была принята комбинация А1. Это правило декодирования для указанного распределения ошибок является оптимальным, так как оно обеспечивает исправление максимального количества ошибок. (В общем случае оптимальное правило декодирования зависит от распределения ошибок.)
Аналогичное правило используется в теории потенциальной помехоустойчивости при оптимальном приеме дискретных сигналов, когда решение сводится к выбору того переданного сигнала, который в наименьшей степени отличается от принятого. Нетрудно определить, что при таком правиле декодирования будут исправлены все ошибки кратности:
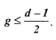 (11.4)
(11.4)
Минимальное значение d , при котором еще возможно исправление любых одиночных ошибок, равно 3.
Возможно также построение таких кодов, в которых часть ошибок исправляется, а часть только обнаруживается. Так, в соответствии с рис. 11.1 в ошибки кратности 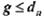 исправляются, а ошибки, кратность которых лежит в пределах
исправляются, а ошибки, кратность которых лежит в пределах 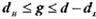 только обнаруживаются. Что касается ошибок, кратность которых сосредоточена в пределах
только обнаруживаются. Что касается ошибок, кратность которых сосредоточена в пределах 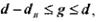 то они обнаруживаются, однако при их исправлении принимается ошибочное решение — считается переданной комбинация
то они обнаруживаются, однако при их исправлении принимается ошибочное решение — считается переданной комбинация 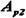 вместо,
вместо, 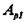 или наоборот. Существуют двоичные системы передачи информации, в которых решающее устройство выдает, кроме обычных символов 0 и 1, еще и так называемый символ стирания
или наоборот. Существуют двоичные системы передачи информации, в которых решающее устройство выдает, кроме обычных символов 0 и 1, еще и так называемый символ стирания 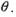 Этот символ соответствует приему сомнительных сигналов, когда затруднительно принять определенное решение в отношении того, какой из символов 0 или 1 был передан. Принятый символ в этом случае стирается. Однако при использовании корректирующего кода возможно восстановление стертых символов. Если в кодовой комбинации число символов
Этот символ соответствует приему сомнительных сигналов, когда затруднительно принять определенное решение в отношении того, какой из символов 0 или 1 был передан. Принятый символ в этом случае стирается. Однако при использовании корректирующего кода возможно восстановление стертых символов. Если в кодовой комбинации число символов 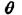 оказалось равным gc, причем
оказалось равным gc, причем
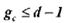 (11.5)
(11.5)
а остальные символы приняты без ошибок, то такая комбинация полностью восстанавливается. Действительно, для восстановления всех символов 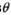 необходимо перебрать всевозможные сочетания из
необходимо перебрать всевозможные сочетания из 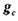 символов типа 0 и 1. Естественно, что все эти сочетания, за исключением одного, будут неверными. Но так как в неправильных сочетаниях кратность ошибок
символов типа 0 и 1. Естественно, что все эти сочетания, за исключением одного, будут неверными. Но так как в неправильных сочетаниях кратность ошибок 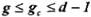 , то согласно неравенству (11.2) такие ошибки обнаруживаются. Другими словами, в этом случае неправильно восстановленные сочетания из
, то согласно неравенству (11.2) такие ошибки обнаруживаются. Другими словами, в этом случае неправильно восстановленные сочетания из 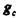 -символов совместно с правильно принятыми символами образуют запрещенные комбинации, и только одно сочетание стертых символов дает разрешенную комбинацию, которую и следует считать как правильно восстановленную.
-символов совместно с правильно принятыми символами образуют запрещенные комбинации, и только одно сочетание стертых символов дает разрешенную комбинацию, которую и следует считать как правильно восстановленную.
Если 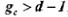 , то при восстановлении окажется несколько разрешенных комбинаций, что не позволит принять однозначное решение.
, то при восстановлении окажется несколько разрешенных комбинаций, что не позволит принять однозначное решение.
Таким образом, при фиксированном кодовом расстоянии максимально возможная кратность корректируемых ошибок достигается в кодах, которые обнаруживают ошибки или восстанавливают стертые символы. Исправление ошибок представляет собой более трудную задачу, практическое решение которой сопряжено с усложнением кодирующих и декодирующих устройств. Поэтому исправляющие коды обычно используются для корректирования ошибок малой кратности.
Корректирующая способность кода возрастает с увеличением d. При фиксированном числе разрешенных комбинаций М0 увеличение d возможно лишь за счет роста количества запрещенных комбинаций:
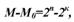 (11.6)
(11.6)
что, в свою очередь, требует избыточного числа символов 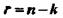 , где к — количество символов в комбинации кода без избыточности. Можно ввести понятие избыточности кода и количественно определить, как:
, где к — количество символов в комбинации кода без избыточности. Можно ввести понятие избыточности кода и количественно определить, как:
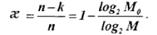 (11.7)
(11.7)
При независимых ошибках вероятность определенного сочетания g ошибочных символов в 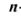 -значной кодовой комбинации выражается формулой (11.3), а количество всевозможных сочетаний ошибочных g-символов в комбинации зависит от ее длины и определяется известной формулой числа сочетаний:
-значной кодовой комбинации выражается формулой (11.3), а количество всевозможных сочетаний ошибочных g-символов в комбинации зависит от ее длины и определяется известной формулой числа сочетаний:
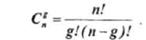
Отсюда полная вероятность ошибки кратности g , учитывающая все сочетания ошибочных символов, равняется:
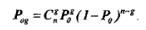 (11.8)
(11.8)
Используя (11.8), можно записать формулы, определяющие вероятность отсутствия ошибок в кодовой комбинации, т. е. вероятность правильного приема:
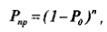
и вероятность правильного корректирования ошибок:
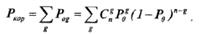
Здесь суммирование производится по всем значениям кратности ошибок g, которые обнаруживаются и исправляются. Таким образом, вероятность некорректируемых ошибок равна:
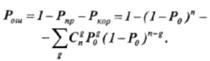 (11.9)
(11.9)
Анализ формулы (11.9) показывает, что при малой величине 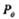 и сравнительно небольших значениях и наиболее вероятны ошибки малой кратности, которые и необходимо корректировать в первую очередь.
и сравнительно небольших значениях и наиболее вероятны ошибки малой кратности, которые и необходимо корректировать в первую очередь.
Вероятность 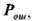 избыточность
избыточность 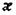 и число символов
и число символов 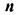 являются основными характеристиками корректирующего кода, определяющими, насколько удается повысить помехоустойчивость передачи дискретной информации и какой ценой это достигается.
являются основными характеристиками корректирующего кода, определяющими, насколько удается повысить помехоустойчивость передачи дискретной информации и какой ценой это достигается.
Общая задача, которая ставится при создании кода, заключается в достижении наименьших значений 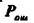 и
и 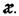
Дата добавления: 2015-04-07; просмотров: 1381;
