Отимальное кодирование.

Возможно ли так закодировать сообщение, чтобы скорость передачи достигала своего максимального значения, равного пропускной способности двоичного канала

Одним из кодов, удовлетворяющих указанному условию, является код Шеннона-Фано.Для ознакомления с принципами его построения рассмотрим в качестве примера источник сообщений, вырабатывающий четыре сообщения 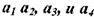с вероятностями: P(a₁),P(a₂),P(a₃),P(a₄).

Все сообщения выписываются в кодовую таблицу (табл. 11.1) в порядке убывания их вероятностей. Затем они разделяются на две группы так, чтобы суммы их вероятностей по возможности были одинаковыми. В данном примере в первую группу входит сообщение а₁ с вероятностью 0,5 и во вторую сообщения с суммарной вероятностью, также равной 0,5.

Таблица 11.1

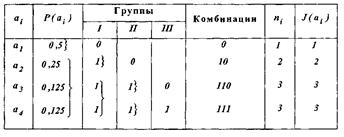
Комбинациям, которые соответствуют сообщениям первой группы, присваивается в качестве первого символа кода — 0, а комбинациям второй группы — 1. Каждая из двух групп опять делится на две группы с применением того же правила присвоения символов 0 и 1. В идеальном случае после первого деления вероятности каждой группы должны быть равны 0,5, после второго деления — 0,25 и т. д. Процесс деления продолжается до тех пор, пока в группах не останется по одному сообщению.

При заданном распределении вероятностей сообщений код получается неравномерным, его комбинации имеют различное число элементов. Причем, как нетрудно заметить, такой способ кодирования обеспечивает выполнение условия оптимальности кода полностью для всех сообщений.

В неравномерных кодах при декодировании возникает трудность в определении границ между комбинациями. Для устранения возможных ошибок обычно применяются специальные разделительные знаки. Так, в коде Морзе между буквами передается разделительный знак в виде паузы длительностью в одно тире. Передача разделительных знаков занимает дополнительное время, что снижает скорость передачи информации.

Важным свойством кода Шеннона-Фано является то, что, несмотря на его неравномерность, здесь не требуются разделительные знаки. Это обусловлено тем, что короткие комбинации не являются началом более длинных. Код является префиксным.

Префиксные коды - это такие коды, в которых ни одна более короткая комбинация не является началом более длинной комбинации, а это позволяет производить однозначное декодирование, даже если последовательность кодов не содержит разделителей между кодами.

Указанное свойство легко проверить на примере любой последовательности:

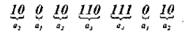
Таким образом, все элементы закодированного сообщения несут полезную информацию, что при выполнении условия оптимальности кода позволяет получить максимальную скорость передачи. Она может быть найдена путем непосредственного вычисления по формуле (11.1):

(11.1)

Для сравнения рассмотрим кодирование тех же четырех сообщений 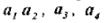с применением обычного равномерного двоичного кода. Количество комбинаций при этом определяется выражением 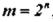, где 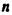- число элементов в комбинации. Так как 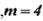, то 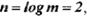а длительность каждой комбинации — 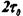. Производя вычисления по аналогии с (11.1), получим:

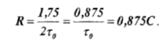
Пропускная способность в этом случае используется только частично.

Основной принцип оптимального кодирования: наиболее вероятным сообщениям должны присваиваться более короткие комбинации, а сообщениям с малой вероятностью — более длинные комбинации.

Одним из способов оптимального кодирования зависимых сообщений является применение так называемых "скользящих" кодов, основная идея которых состоит в том, что присвоение кодовых комбинаций по правилу Шеннона-Фано производится с учетом условных, а не априорных вероятностей сообщений. Число элементов в кодовой комбинации выбирается как 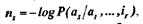т.е. текущему сообщению присваивается та или иная комбинация в зависимости от того, какие сообщения ему предшествовали.

Необходимо подчеркнуть, что при оптимальном способе кодирования в сигналах, передающих сообщения источника, совершенно отсутствует какая-либо избыточность. Устранение избыточности приводит к тому, что процесс декодирования становится весьма чувствительным к воздействию помех. Это особенно сильно проявляется при оптимальном кодировании зависимых сообщений. Например, в "скользящих" кодах одна-единственная ошибка может вызывать неправильное декодирование всех последующих сигналов. Поэтому оптимальные коды применимы только для каналов, в которых влияние помех незначительно.

Принцип построения оптимальных кодов:

1. Каждый элементарный символ должен переносить максимальное количество информации, для этого необходимо, чтобы элементарные символы (0 и 1) в закодированном тексте встречались в среднем одинаково часто. Энтропия в этом случае будет максимальной.

2. Необходимо буквам первичного алфавита, имеющим большую вероятность, присваивать более короткие кодовые слова вторичного алфавита.