Примеры анализа диагностических моделей
Пример 1. ДМ в виде ориентированного графа. Если ОД представлен специальной ДМ в виде ориентированного графа, то решить задачу выбора совокупности оцениваемых диагностических параметров можно следующим образом.
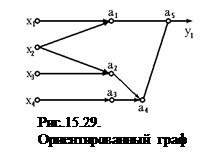
Ранжировать вершины графа (диагностические параметры) по правилу: всем вершинам, имеющим в качестве входов только множества х1,...,хn, присваивается ранг 1; затем любой вершине, имеющей в качестве входов входы из множества х1,...,хn, и выходы вершин с рангом 1, присваивается ранг 2 и т.д.
Для ориентированного графа (рис.15.29) рангами вершин будут: u(а1) = u(а2) = u(а3) = 1; u(а4) = 2; u(а5) = 3.
Пусть для простоты ki = 1, ci = 1, 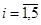 (15.6) и необходимо обеспечить методическую составляющую достоверности Р0
(15.6) и необходимо обеспечить методическую составляющую достоверности Р0 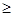 0.9.
0.9.
Рассчитаем р(n) при исключении одного из параметров с рангом 1. Получим р(а5,а4,а3,а2) = 7/8 = 0,88 < Ро.
Следовательно, для ОД исключить из рассмотрения хотя бы один параметр невозможно. Для обеспечения заданной достоверности необходимо оценивать все диагностические параметры
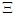 = (а1,а2,а3,а4,а5).
= (а1,а2,а3,а4,а5).
Развитие этого подхода предполагает введение весовых коэффициентов для вершин с учетом стоимости, времени измерения и т.д.
 Пример 2. Информационная ДМ. Решить задачу упорядочения диагностических параметров можно используя информационный критерий вида:
Пример 2. Информационная ДМ. Решить задачу упорядочения диагностических параметров можно используя информационный критерий вида:
Ij = Iбj + Iсj,
где Iбj – составляющая, учитывающая свойства j-го параметра через безотказность элементов; Iсj – составляющая, учитывающая структурные свойства j-го параметра.
Рассмотрим каждую составляющую отдельно.
Первую составляющую можно определить через показатель надежности элементов объекта, состояние которых определяется через j-й параметр
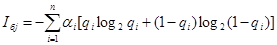 ,
,
где  – коэффициенты значимости (вес) i-го элемента, формирующего j-й параметр,
– коэффициенты значимости (вес) i-го элемента, формирующего j-й параметр,  ; qi –вероятность отказа i-го элемента, формирующего
; qi –вероятность отказа i-го элемента, формирующего
j-й параметр,(qi = 1-рi,где рi – вероятность безотказной работы i-го элемента за рассматриваемый интервал времени); n – число элементов объекта, изменение состояния которых чувствуется j-м параметром.
Это можно пояснить на следующем примере (рис. 15.30).
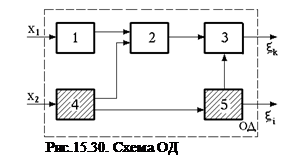 Параметр
Параметр  чувствителен только к изменению состояния 4-го и 5-го элементов при условии подачи на вход ОД нормальных входных сигналов х1 и х2.
чувствителен только к изменению состояния 4-го и 5-го элементов при условии подачи на вход ОД нормальных входных сигналов х1 и х2.
В качестве величины  , характеризующей значимость i-го элемента, можно использовать выражение:
, характеризующей значимость i-го элемента, можно использовать выражение:
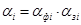 ,
,
где 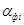 – функциональная значимость i-го элемента;
– функциональная значимость i-го элемента;  – значимость по затратам на изготовление и восстановление состояния i-го элемента.
– значимость по затратам на изготовление и восстановление состояния i-го элемента.
Определить 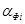 можно, воспользовавшись матрицей связанности вида
можно, воспользовавшись матрицей связанности вида
| s1 | s2 | ... | sn | |
| s1 | 1 | 0 | 1 | |
| s2 | 0 | 1 | 1 | |
| ... | ||||
| sn | 0 | 1 | 1 |
Число строк равно числу столбцов, которое определяется числом СЕ, элементов ОД. Таблица заполняется по правилу: если i-й элемент связан с k-м элементом, то ставится 1, в противном случае – 0.
Ранг Ri определяется как сумма всех единиц в i-й строке. С учетом величины Ri определяется коэффициент функциональной значимости:
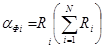 .
.
Дата добавления: 2015-06-10; просмотров: 813;
