Движение носителей тока
Носители тока в твёрдых телах находятся в непрерывном движении. В отсутствие внешнего электрического поля это тепловое хаотическое движение, которое происходит тем более энергично, чем выше температура кристалла. Как известно, закономерности теплового движения являются статистическими. Для носителей тока в полупроводниках при комнатных и более высоких температурах оказывается применимой статистика Максвелла-Больцмана. Из распределения Максвелла следует, что средняя тепловая скорость носителей равна:
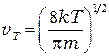 (22)
(22)
При 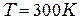 средняя скорость электронов из (22) равна примерно 105 м/с.
средняя скорость электронов из (22) равна примерно 105 м/с.
В металлах из-за очень большой концентрации свободных электронов статистика Максвелла-Больцмана неприменима, и требуется переход к квантовой статистике Ферми. При этом средняя скорость электронов при комнатной температуре оказывается на порядок большей: 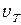 = 106 м/с.
= 106 м/с.
Хаотичность движения обеспечивается столкновениями электронов с решеткой кристалла, происходящими с громадной частотой: 1012 – 1013 раз в секунду. Количественной характеристикой столкновений является среднее время между столкновениями 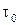 , которое называют также временем релаксации. Таким образом, время релаксации носителей в полупроводниках
, которое называют также временем релаксации. Таким образом, время релаксации носителей в полупроводниках 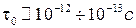 на несколько порядков меньше их времени жизни.
на несколько порядков меньше их времени жизни.
Если к кристаллу приложено электрическое поле, то дополнительно появляется пусть слабое, по сравнению с тепловым, но направленное движение носителей, то есть электрический ток.
Электрическое поле действует на электрон с силой 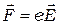 и сообщает ему ускорение
и сообщает ему ускорение  . Дрейфовую скорость электрона можно оценить как произведение ускорения на среднее время между столкновениями
. Дрейфовую скорость электрона можно оценить как произведение ускорения на среднее время между столкновениями 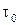 :
:
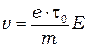 (23)
(23)
Сравнивая (23) и (2), получаем соотношение для подвижности:
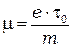 (24)
(24)
Таким образом, подвижность носителей определяется частотой их столкновений с кристаллической решеткой. С увеличением температуры растёт амплитуда тепловых колебаний атомов в узлах кристаллической решетки и увеличивается вероятность столкновений носителей, т.е. уменьшается их подвижность. Расчеты показывают, что приближенно 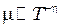 при этом для металлов
при этом для металлов 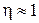 , для полупроводников
, для полупроводников 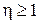 .
.
Значения подвижностей носителей в типичных полупроводниках приведены в табл. 1. Пользуясь этими данными, можно вернуться к вопросу о пределах применимости соотношения (2) и, в конечном счёте, закона Ома. Как следует из (24), подвижность не зависит от внешнего электрического поля до тех пор, пока с увеличением поля не меняется характер столкновений, т.е. пока 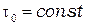 , а следовательно, пока направленное движение не нарушает хаотичности теплового движения, т.е.
, а следовательно, пока направленное движение не нарушает хаотичности теплового движения, т.е. 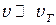 . При комнаткой температуре тепловая скорость в полупроводнике
. При комнаткой температуре тепловая скорость в полупроводнике 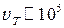 м/с и условию
м/с и условию 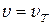 соответствует поле
соответствует поле 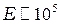 В/м (принято
В/м (принято 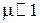 м2/В·с). Таким образом, закон Ома справедлив для полупроводников при условия
м2/В·с). Таким образом, закон Ома справедлив для полупроводников при условия 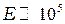 В/м. Для металлов из-за большей тепловой скорости и меньшей подвижности электронов эта область расширяется еще на несколько порядков. В подавляющем большинстве технических устройств электрические поля далеки от предельных, и поэтому закон Ома имеет весьма широкую область применения.
В/м. Для металлов из-за большей тепловой скорости и меньшей подвижности электронов эта область расширяется еще на несколько порядков. В подавляющем большинстве технических устройств электрические поля далеки от предельных, и поэтому закон Ома имеет весьма широкую область применения.
Дата добавления: 2015-06-10; просмотров: 941;
