Построение окружностей в прямоугольной изометрической проекции

На рис. 73 приведены комплексные чертежи окружностей, лежащих в координатных плоскостях: хОу, xOz и yOz.

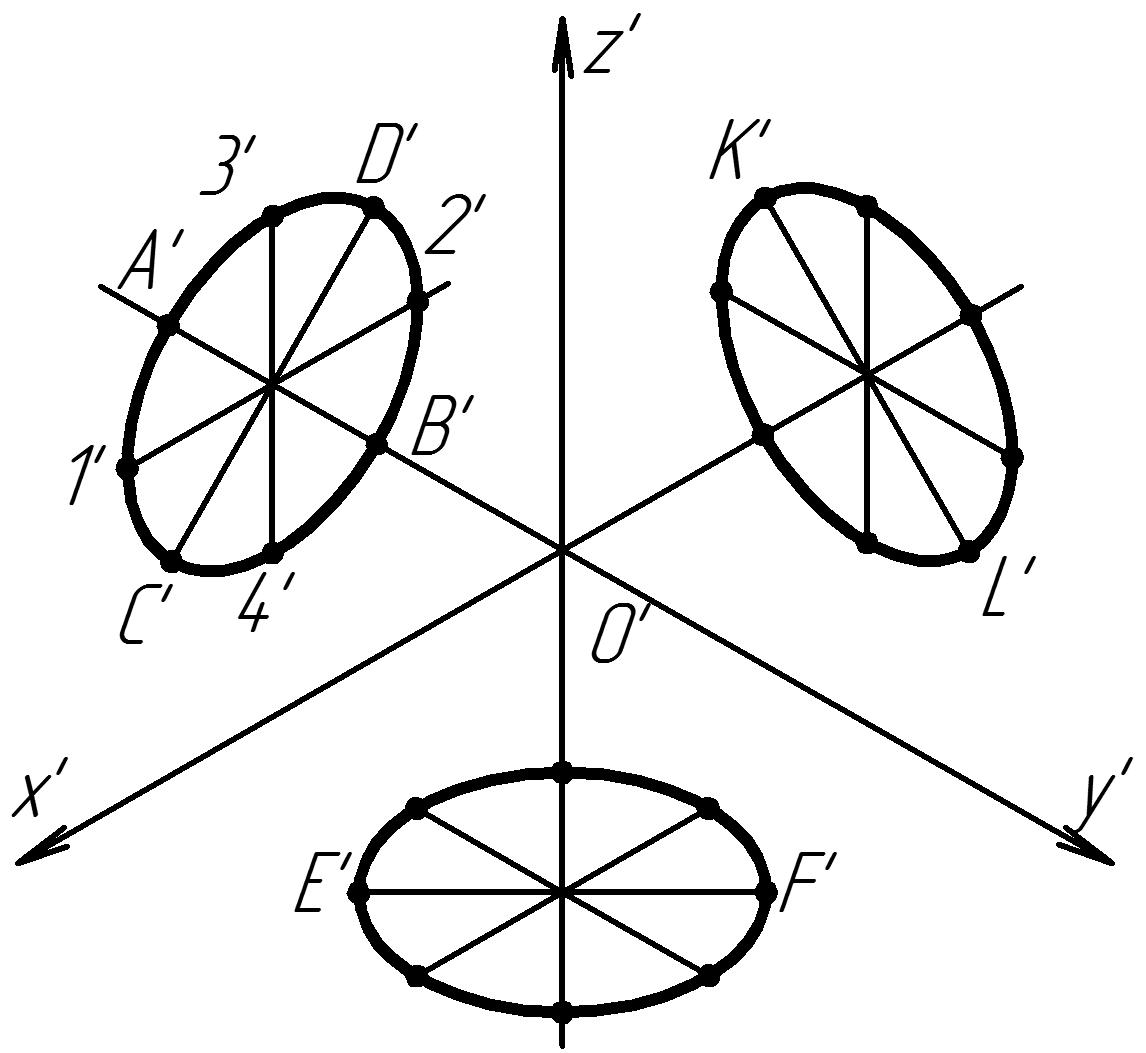
Рис. 73 Построение окружностей в прямоугольной изометрии

Проекция окружности в общем случае есть эллипс. В приведенной прямоугольной изометрической проекции длина большой оси эллипса равна 1,22 диаметра окружности, длина малой оси эллипса равна 0,7 диаметра окружности. Рассмотрим построение изометрической проекции окружности, лежащей в плоскости xOz. Сначала строят проекцию центра окружности по координатам х и z. Через построенную точку проводят линии, параллельные осям х' и z', на которых, откладывая натуральную величину радиуса окружности, находят проекции 1', 2', 3' и 4'.

Проводят направление большой оси эллипса перпендикулярно оси у' и откладывают на нем размер, равный 1,22d (С'D'). Перпендикулярно большой оси эллипса (параллельно оси у') строят, малую ось эллипса (А'В') длиной 0,7d. Найденные точки соединяют плавной кривой. Аналогично производят построение эллипсов, являющихся изометрическими проекциями окружностей, лежащих в плоскостях хОу и yOz. Следует запомнить, что направление большой оси эллипса перпендикулярно аксонометрической оси, не лежащей в плоскости, к которой относится эллипс (С'D'^y', E'F'^z', K'L'^x').

Обычно для упрощения построения аксонометрических проекций эллипсы заменяют очень близкими им по начертанию овалами.

<34 35 363738 39 40 >

Дата добавления: 2015-06-05; просмотров: 2182;