Теорема о циркуляции при наличии магнетиков. Граничные условия для магнетиков.
В вакууме: 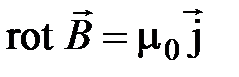 (см. систему уравнений (3.29-3.30)).
(см. систему уравнений (3.29-3.30)).
При наличии магнетиков при 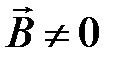 появляется намагниченность
появляется намагниченность 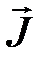 . Механизм появления
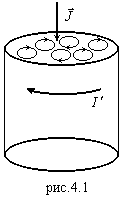
. Механизм появления 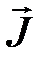 связан с магнитными моментами атомов, создаваемыми движущимися по орбите электронами. Такое движение можно уподобить элементарным замкнутым токам, названным молекулярными. Молекулярные токи могут привести к появлению макроскопических токов намагничивания. Это видно из следующего примера. Рассмотрим цилиндр из однородного магнетика, намагниченного вдоль оси. Ориентация молекулярных токов показана на рис.4.1. Видно, что внутри соседние токи компенсируют друг друга. На поверхности же образуется поверхностный ток намагничивания, циркулирующий по боковой поверхности цилиндра. Ток
связан с магнитными моментами атомов, создаваемыми движущимися по орбите электронами. Такое движение можно уподобить элементарным замкнутым токам, названным молекулярными. Молекулярные токи могут привести к появлению макроскопических токов намагничивания. Это видно из следующего примера. Рассмотрим цилиндр из однородного магнетика, намагниченного вдоль оси. Ориентация молекулярных токов показана на рис.4.1. Видно, что внутри соседние токи компенсируют друг друга. На поверхности же образуется поверхностный ток намагничивания, циркулирующий по боковой поверхности цилиндра. Ток  создает такое же магнитное поле, как и все молекулярные токи.
создает такое же магнитное поле, как и все молекулярные токи.
 Если магнетик неоднородный, то останется не скомпенсированным и ток в объеме, т.е. возникнет и объемный макроскопический ток
Если магнетик неоднородный, то останется не скомпенсированным и ток в объеме, т.е. возникнет и объемный макроскопический ток  .
.
Вычислим циркуляцию вектора намагниченности по замкнутому контуру внутри магнетика. Натянем на контур 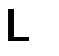 поверхность S (см. рис.4.2). Видно, что внутри молекулярные токи пересекают поверхность дважды в разных направлениях. Такие токи не вносят вклад в циркуляцию
поверхность S (см. рис.4.2). Видно, что внутри молекулярные токи пересекают поверхность дважды в разных направлениях. Такие токи не вносят вклад в циркуляцию 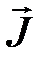 по контуру
по контуру 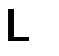 .
.
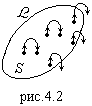 Те токи, которые обвивают контур, пересекают поверхность один раз и создают намагниченность
Те токи, которые обвивают контур, пересекают поверхность один раз и создают намагниченность 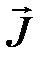 (рис.4.2). Намагниченность
(рис.4.2). Намагниченность 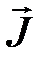 образует с элементом контура
образует с элементом контура 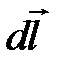 угол
угол 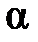 . Поэтому
. Поэтому 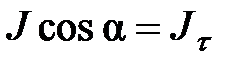 и тогда:
и тогда:
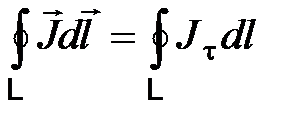 , (4.3)
, (4.3)
 где
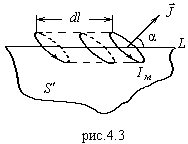
где 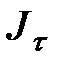 - тангенциальная составляющая вдоль контура интегрирования. Токи, пересекающие поверхность на элементе длины контура
- тангенциальная составляющая вдоль контура интегрирования. Токи, пересекающие поверхность на элементе длины контура 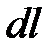 - это токи внутри цилиндра (рис.4.3) объема
- это токи внутри цилиндра (рис.4.3) объема 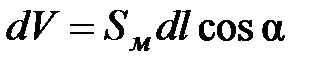 ,
, 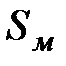 - площадь одного витка, по которому течет ток
- площадь одного витка, по которому течет ток 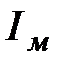 . Ток внутри цилиндра на рис.4.3:
. Ток внутри цилиндра на рис.4.3:
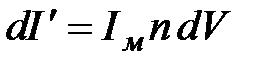 , (4.4)
, (4.4)
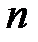 - концентрация токов
- концентрация токов 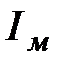 .
.
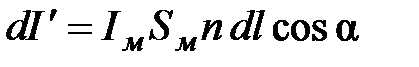 . (4.5)
. (4.5)
Учтем, что магнитный момент витка: 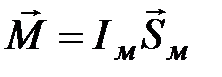 , тогда:
, тогда:
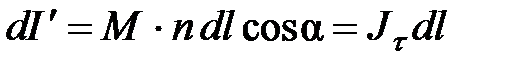 , (4.6)
, (4.6)
где учтено, что 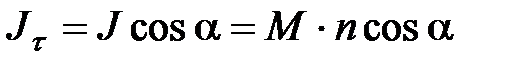 , поэтому при интегрировании (4.6) получим:
, поэтому при интегрировании (4.6) получим:
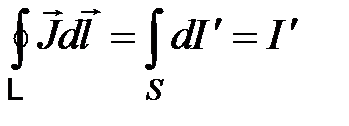 , (4.7)
, (4.7)
где 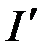 - сумма токов намагничивания (поверхностных для однородного магнетика), пересекающих поверхность, натянутую на контур
- сумма токов намагничивания (поверхностных для однородного магнетика), пересекающих поверхность, натянутую на контур 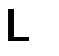 .
.
Для неоднородного магнетика:
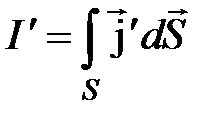 , (4.8)
, (4.8)
где 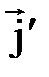 - плотность молекулярного тока. Интегрирование распространяется на всю поверхность S, натянутую на контур
- плотность молекулярного тока. Интегрирование распространяется на всю поверхность S, натянутую на контур 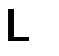 . Записав:
. Записав:
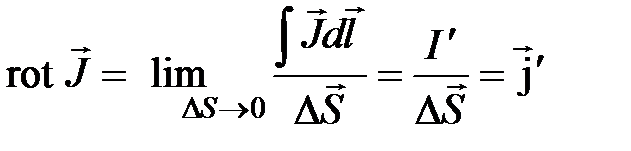 , (4.9)
, (4.9)
получим в дифференциальной форме получим:
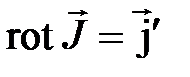 .
.
(4.10)
В магнетиках, помещенных во внешнее поле, возникают токи намагничивания 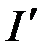 , поэтому уравнение
, поэтому уравнение 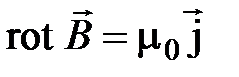 должно учесть не только токи проводимости, но и токи намагничивания.
должно учесть не только токи проводимости, но и токи намагничивания.
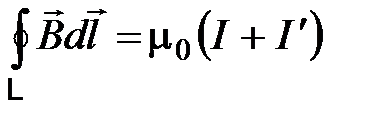 , (4.11)
, (4.11)
где 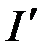 - токи намагничивания, охватываемые контуром
- токи намагничивания, охватываемые контуром  .
.
Так как токи 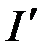 могут быть определены из циркуляции
могут быть определены из циркуляции 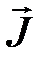 , можно ввести некоторый вспомогательный вектор
, можно ввести некоторый вспомогательный вектор 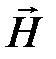 , чтобы отделить влияние
, чтобы отделить влияние 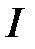 и
и 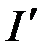 . Лучше всего это сделать в уравнениях в дифференциальной форме.
. Лучше всего это сделать в уравнениях в дифференциальной форме.
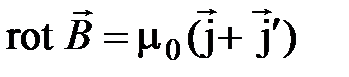 . (4.12)
. (4.12)
С учетом (4.10):
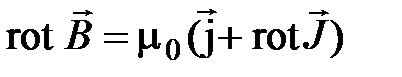 , (4.13)
, (4.13)
откуда:
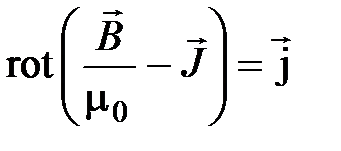 . (4.14)
. (4.14)
Величину в скобках назовем вектором напряженности магнитного поля 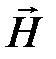 :
:
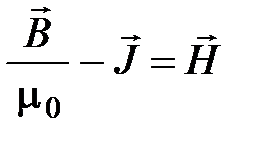 , (4.15)
, (4.15)
или: 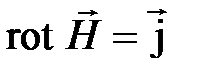 или
или 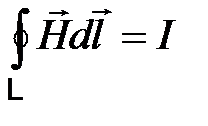 . (4.16)
. (4.16)
Таким образом, вектор магнитной индукции есть сумма двух векторов:
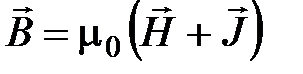 . (4.17)
. (4.17)
Введем величину магнитной проницаемости 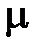 :
:
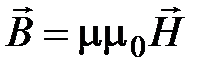 (4.18)
(4.18)
и магнитной восприимчивости 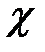 :
:
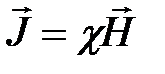 . (4.19)
. (4.19)
Величина магнитной восприимчивости вещества связана с магнитной проницаемостью следующим соотношением, полученным из (4.17):
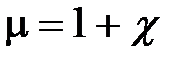 . (4.20)
. (4.20)
В зависимости от знака и величины восприимчивости магнетики разделяются на следующие типы:
1. Диамагнетики: 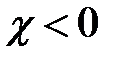 , следовательно
, следовательно  .
.
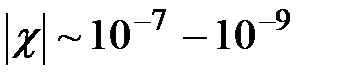 .
.
2. Парамагнетики 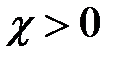 , следовательно
, следовательно  .
.
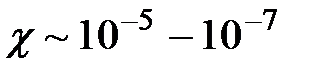 .
.
3. Ферромагнетики. 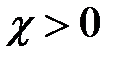 ,
, 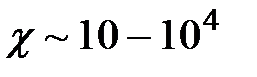 .
.
Из определения вектора 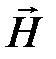 видно, что размерности
видно, что размерности 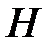 и
и  одинаковы. Размерность
одинаковы. Размерность 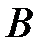 в системе СИ – Тл (Тесла), размерность
в системе СИ – Тл (Тесла), размерность 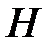 и
и  - А/м (см. (4.16)). Поэтому восприимчивость
- А/м (см. (4.16)). Поэтому восприимчивость 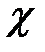 (видно из (4.20))- безразмерная величина.
(видно из (4.20))- безразмерная величина.
Итог:
теорема о циркуляции при наличии магнетиков записывается в виде трех уравнений:
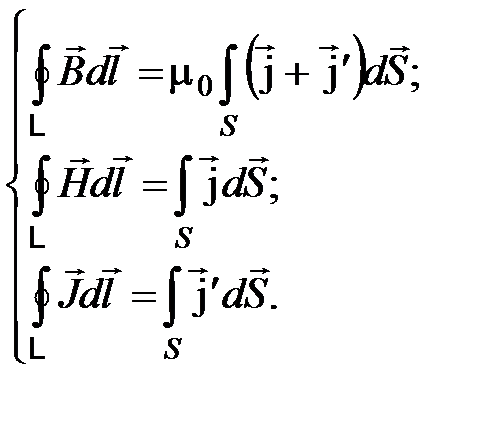 (4.21)
(4.21)
или в дифференциальной форме:
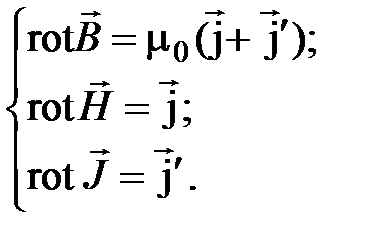 (4.22)
(4.22)
Отсюда получим граничные условия для 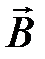 и
и 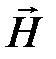 .
.
 Из
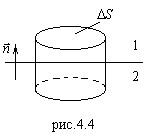
Из 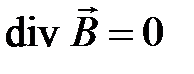 (см.рис.4.4) следует, что:
(см.рис.4.4) следует, что:
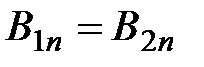 . (4.23)
. (4.23)
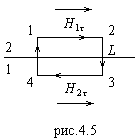
Из второго уравнения (4.21) и рис.4.5 получаем:
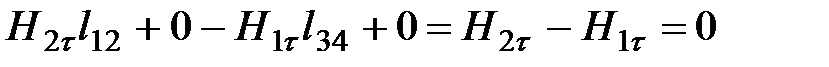 ;
;
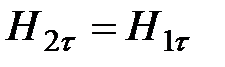 (4.24)
(4.24)
при 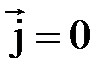 , т.е. в отсутствии токов проводимости.
, т.е. в отсутствии токов проводимости.
Остальные компоненты 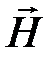 и
и 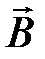 претерпевают скачки, так как
претерпевают скачки, так как 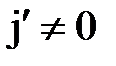 всегда.
всегда.
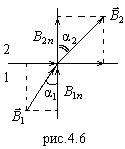 Поэтому на границе раздела векторы
Поэтому на границе раздела векторы 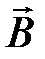 и
и 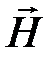 преломляются (см. рис.4.6). Из (4.23) (и (4.24):
преломляются (см. рис.4.6). Из (4.23) (и (4.24):
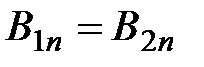 ,
, 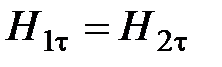 .
.
Но при 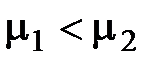
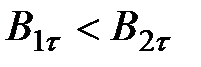 , т.к.:
, т.к.:
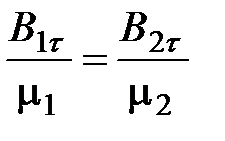 . (4.25)
. (4.25)
Следовательно: 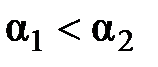 , т.к.:
, т.к.:
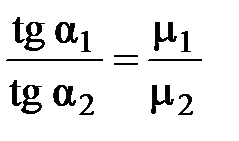 . (4.26)
. (4.26)
Задача.
Найти условия, при которых внутри магнетика отсутствуют токи намагничивания, т.е. 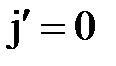 .
.
1. Магнетик должен быть однородным (это уже было показано выше), чтобы 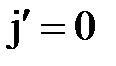 .
.
2. По теореме о циркуляции вектора 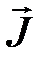 (третье уравнение (4.21)) найдем второе условие для
(третье уравнение (4.21)) найдем второе условие для 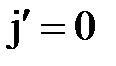 .
.
Выберем контур 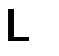 внутри магнетика. Для однородного магнетика
внутри магнетика. Для однородного магнетика 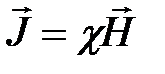 . Тогда последнее выражение (4.21) перепишется в виде:
. Тогда последнее выражение (4.21) перепишется в виде:
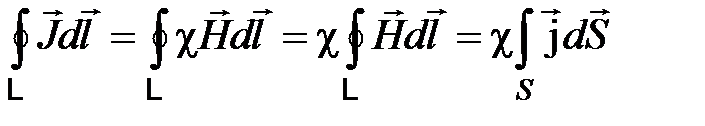 .
.
Отсюда:
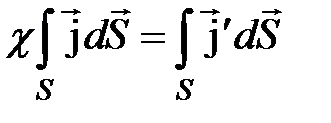 . (4.27)
. (4.27)
При переходе к плотности токов:
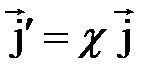 . (4.28)
. (4.28)
Таким образом, векторы 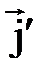 и
и 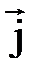 параллельны (
параллельны ( 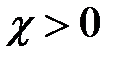 ). Отсюда следует, что
). Отсюда следует, что 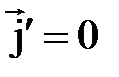 при
при 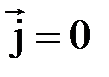 , т.е. в отсутствии токов проводимости.
, т.е. в отсутствии токов проводимости.
Результат целесообразно сравнить с результатом (2.41) задачи о диэлектрике (при 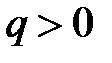 ):
):
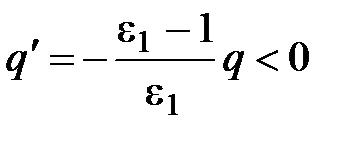 .
.
Дата добавления: 2015-06-01; просмотров: 1551;
