Основные законы магнитного поля.
Для электрического поля в вакууме были выведены две важнейшие теоремы:
-теорема Гаусса  ,
,
-теорема о циркуляции  .
.
Найдем аналогичные соотношения для 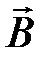 .
.
 Рассмотрим магнитный поток через произвольную замкнутую поверхность. Пусть ток
Рассмотрим магнитный поток через произвольную замкнутую поверхность. Пусть ток  направлен к нам, перпендикулярно плоскости рисунка. Силовые линии – окружности, части которых приведены на рис.3.10. Нарисуем произвольную замкнутую поверхность. Выберем на ней элементарную трубку
направлен к нам, перпендикулярно плоскости рисунка. Силовые линии – окружности, части которых приведены на рис.3.10. Нарисуем произвольную замкнутую поверхность. Выберем на ней элементарную трубку  . Потоки через сечения
. Потоки через сечения  и
и  равны и противоположны по знаку. Общий поток через трубку равен нулю. Всю поверхность можно разбить на такие трубки, то есть:
равны и противоположны по знаку. Общий поток через трубку равен нулю. Всю поверхность можно разбить на такие трубки, то есть:

 . (3.23)
. (3.23)
Это теорема Гаусса для вектора 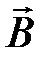 . Из соотношения (3.23) следует, что магнитные заряды отсутствуют. Линии
. Из соотношения (3.23) следует, что магнитные заряды отсутствуют. Линии 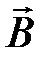 не имеют начала и конца, они либо замкнуты, либо уходят на бесконечность.
не имеют начала и конца, они либо замкнуты, либо уходят на бесконечность.
Сравнение с теоремой Гаусса для электрического поля приводит к возникновению вопроса о магнитных зарядах. В качестве магнитного заряда можно рассматривать  и
и  полюса магнитного диполя. Квантуются ли магнитные заряды, неизвестно. Это незнание следует из невозможности выделения изолированных полюсов: магнитные полюса существуют в природе лишь в виде диполей.
полюса магнитного диполя. Квантуются ли магнитные заряды, неизвестно. Это незнание следует из невозможности выделения изолированных полюсов: магнитные полюса существуют в природе лишь в виде диполей.
В 1931 г. Дирак выдвинул теоретическое предположение в пользу возможности существования квантованного магнитного заряда (монополя), величина которого связана с зарядом электрона как:  . Предполагалось, что существует элементарная частица, подобная электрону, несущая магнитный заряд
. Предполагалось, что существует элементарная частица, подобная электрону, несущая магнитный заряд  . При этом должно выполняться следующее соотношение масс:
. При этом должно выполняться следующее соотношение масс:
 .
.
Экспериментального доказательства существованию монополя до сих пор нет.
 Теперь рассмотрим теорему о циркуляции для
Теперь рассмотрим теорему о циркуляции для 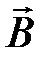 . Будем исходить из выражения (3.16), полученного для индукции магнитного поля тока, текущего по бесконечному прямолинейному проводнику (рис.3.11). Силовые линии – концентрические окружности с центром на линии токов. Величина
. Будем исходить из выражения (3.16), полученного для индукции магнитного поля тока, текущего по бесконечному прямолинейному проводнику (рис.3.11). Силовые линии – концентрические окружности с центром на линии токов. Величина 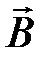 :
:

Вычислим  по произвольному контуру
по произвольному контуру 
 , лежащему в плоскости, содержащей силовые линии
, лежащему в плоскости, содержащей силовые линии 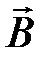 .
.
 ;
;  ;
;

 , (3.24)
, (3.24)
так как  . Если
. Если  не охватывает ток
не охватывает ток  , то, как видно из рис.3.12:
, то, как видно из рис.3.12:
 .
.
Итак:

При большом числе токов в контуре, охватывающем часть из них, в силу принципа суперпозиции 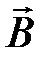 в каждой точке.
в каждой точке.

 . (3.25)
. (3.25)
В общем случае, теорема о циркуляции вектора 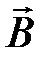 , или закон полного тока, записывается:
, или закон полного тока, записывается:
 , (3.26)
, (3.26)
где  - полный ток (или сумма токов), охватываемый контуром
- полный ток (или сумма токов), охватываемый контуром  . Выведем его в дифференциальной форме. Учтем, что:
. Выведем его в дифференциальной форме. Учтем, что:
 ;
;
 ;
;
 , (3.27)
, (3.27)
или
 . (3.28)
. (3.28)
Это - дифференциальная форма закона полного тока. В такой форме он имеет локальный характер и справедлив в любой точке.
Из закона о циркуляции следует, что магнитное поле не потенциально. Так как силовые линии поля замкнуты, то оно является вихревым.
Следующие четыре уравнения для  совместно носят название уравнений Максвелла для вакуума:
совместно носят название уравнений Максвелла для вакуума:
 ; (3.29)
; (3.29)
 . (3.30)
. (3.30)
Физический смысл этих уравнений таков.
- Уравнения (3.29) описывают тот факт, что силовые линии электрического поля начинаются на положительных зарядах и заканчиваются на отрицательных; силовые линии магнитного поля замкнуты (поле вихревое).
- Уравнения (3.30) показывают, что электростатическое поле потенциально; магнитное поле, создаваемое токами (движущимися зарядами), не потенциальное, вихревое.
Сравним еще раз также формулы для электрического и магнитного диполей и полей на их оси:
 (3.31)
(3.31)
Видно, что магнитные и электрические диполи ведут себя одинаково. Почему? Потому что при  и
и  , то есть вдали от зарядов и токов, уравнения Максвелла одинаковы (правые части
, то есть вдали от зарядов и токов, уравнения Максвелла одинаковы (правые части  и
и  обоих векторов равны нулю). Но физически источники этих полей различны: циркулирующий ток, пара зарядов.
обоих векторов равны нулю). Но физически источники этих полей различны: циркулирующий ток, пара зарядов.
Примеры.
1. По проводу круглого сечения радиуса  течет ток плотности
течет ток плотности  . Найти
. Найти  .
.
Используем теорему о циркуляции вектора 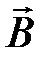 (3.26):
(3.26):
Выберем контур  так, чтобы он проходил по силовой линии магнитного поля (в данной задаче – это окружность). Рассмотрим два случая.
так, чтобы он проходил по силовой линии магнитного поля (в данной задаче – это окружность). Рассмотрим два случая.
1. Радиус контура  . Ток внутри контура
. Ток внутри контура  . Тогда:
. Тогда:
 . (3.32 а)
. (3.32 а)
В векторной форме:
 .
.
2.  Радиус контура
Радиус контура  . Так как ток течет лишь по сечению провода, то
. Так как ток течет лишь по сечению провода, то  .
.

В векторной форме:
 . (3.32 б)
. (3.32 б)
График зависимости  приведен на рис.3.13.
приведен на рис.3.13.
2. Найти индукцию магнитного поля тороида (  и
и  - радиусы).
- радиусы).
Силовые линии – окружности, центр которых в центре тора. Ясно, что там, где нет витков, то есть при  ,
,  . При
. При 
 . (3.33)
. (3.33)
При  :
:  , так как ток пересекает площадь контура дважды в различных направлениях.
, так как ток пересекает площадь контура дважды в различных направлениях.
Дата добавления: 2015-06-01; просмотров: 2068;
