Линеаризация дифференциальных уравнений

Подавляющее большинство реальных элементов имеют нелинейные характеристики и, следовательно, описываются нелинейными дифференциальными уравнениями. Однако, многие нелинейные элементы можно линеаризовать, то есть заменить нелинейные уравнения элемента приближенными линейными. Это позволяет для анализа и синтеза систем управления использовать методы теории линейных систем, которые наиболее просты и хорошо разработаны. В основе линеаризации нелинейных уравнений лежит предположение, что в исследуемом динамическом процессе переменные координаты системы изменяются таким образом, что их отклонения от установившихся значений остаются все время достаточно малыми величинами. Это условие выполняется для замкнутых систем, так как последние работают по принципу ликвидации ошибки.

Геометрическая трактовка линеаризации. Изобразим графически нелинейную зависимость (рис. 2.1)

y(t) = F(x(t)) . (2.1)

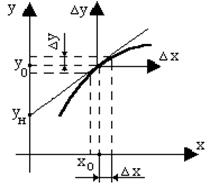
Рис. 2.1. Геометрическая интерпретация линеаризации

Текущие значения координат y и x запишем как

y(t) = y₀ + Dy(t);

x(t) = x₀ + Dx(t);

где y₀, x₀ – установившиеся значения, Dy, Dx – их отклонения от установившихся значений.

В рабочей точке ( x₀, y₀), определяемой установившимися значениями, заменим участок кривой касательной и получим прямую, описываемую линейным уравнением

y = y_н + kx ,

где y_{н -} постоянная величина;

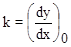- коэффициент, определяемый наклоном касательной к кривой в рабочей точке ( x₀, y₀).

Для исключения из уравнения величины y_н перенесем начало координат в рабочую точку. Тогда получим линейное уравнение, связывающее между собой отклонения переменных величин от своих установившихся значений, вида

Dy(t) = k Dx(t) . (2.2)

Таким образом, линеаризация уравнения геометрически может трактоваться как замена первоначальной кривой на касательную к ней прямую в точке установившегося режима. Очевидно, что эта замена тем точнее, чем меньше величины отклонений координат элемента от своих установившихся значений в исследуемом динамическом процессе.

В общем случае при составлении уравнения динамики элемента системы (рис. 2.2), имеющего входную величину x, выходную - y и внешнее воздействие f, получается динамическое уравнение произвольного нелинейного вида

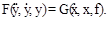(2.3)

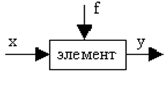
Рис. 2.2. Элемент автоматической системы

Допустим, что установившиеся значения переменных y, x и f являются постоянными величинами y₀, x₀, f₀, характеризующими установившийся режим и определяющими рабочую точку элемента.

Тогда для текущих координат можно записать

y(t) = y₀ + Dy(t);

x(t) = x₀ + Dx(t);

f(t) = f₀ + Df(t);

где Dy, Dx, Df – отклонения y, x, f от своих установившихся значений.

Из (2.3) получается уравнение статики

F(y₀) = G(x₀, f₀) . (2.4)

Для линеаризации уравнения (2.3) последнее раскладывают в ряд Тейлора по степеням отклонений всех координат элемента от своих установившихся значений. Тогда уравнение (2.3) примет вид

+ (члены высшего порядка малости). (2.5)

Вычитая из последнего уравнения (2.5) уравнение статики (2.4) и отбросив все последующие члены разложения как малые высшего порядка, придем к линейному уравнению динамики элемента

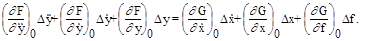(2.6)

Здесь нижний индекс “0” обозначает, что значения частных производных должны быть определены в точке установившегося режима элемента.

Это дифференциальное уравнение, так же как и (2.3), описывает тот же динамический процесс в том же элементе автоматической системы. Сравним (2.3) и (2.6):

уравнение (2.3) - точное, а уравнение (2.6) - приближенное, ибо в процессе его получения были отброшены малые высшего порядка;

уравнение (2.3) записано относительно переменных величин элемента, а уравнение (2.6) - относительно отклонений переменных от своих установившихся значений;

уравнение (2.3) - нелинейное, уравнение (2.6) - линейное относительно отклонений, коэффициенты которого определяются рабочей точкой элемента, то есть его установившимися значениями; при смене рабочей точки эти коэффициенты изменяются.

Таким образом, цель получения линейного дифференциального уравнения взамен прежнего нелинейного достигнута. Уравнение (2.6) называется дифференциальным уравнением элемента в отклонениях.

Ограничение метода. Данным методом могут быть линеаризованы уравнения элементов, статические характеристики которых в окрестности точки установившегося режима гладкие, то есть их производные непрерывны и однозначны. Не могут быть линеаризованы уравнения элементов с негладкими, неоднозначными и имеющими разрывы в окрестности точки установившегося режима статическими характеристиками.

Замечание: в дальнейшем будем использовать только линеаризованные уравнения, записанные относительно отклонений от установившихся значений переменных, однако для сокращения записи знак “D” будем опускать.

Пример. Электромагнитный момент M электродвигателя постоянного тока с независимым возбуждением определяется нелинейным уравнением

M = c Iя Iв,

где c - постоянный коэффициент;

Iя, Iв - токи, протекающие в цепях якоря и возбуждения.

Решение. Линеаризуем выражение для M разложением в ряд Тэйлора и учетом лишь линейных составляющих ряда. В результате получим соотношение для малых приращений

(¶M/¶M)₀ DM = (¶(c Iя Iв)/¶Iя)₀ DIя + (¶(c Iя Iв)/¶Iв)₀ DIв.

Откуда следует

DM = c Iв₀ DIя + c Iя₀ DIв _.

Здесь нижним индексом “0” обозначены установившиеся значения переменных, относительно которых изменяются их приращения.