Позиционные звенья

В звеньях позиционного, или статического типа, линейной зависимостью y = kx связаны выходная и входная величины в установившемся режиме. Коэффициент пропорциональности k между выходной и входной величинами представляет собой коэффициент передачи звена. Позиционные звенья обладают свойством самовыравнивания, то есть способностью самостоятельно переходить в новое установившееся состояние при ограниченном изменении входного воздействия.

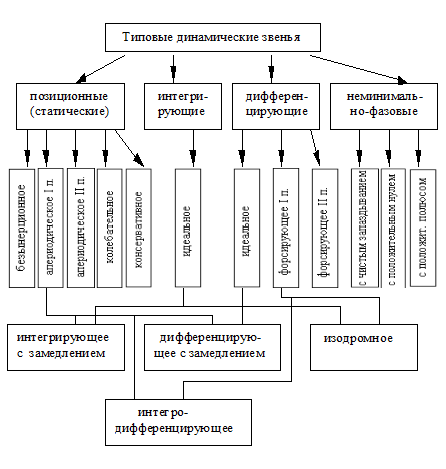Рис. 3.9. Классификация типовых динамических звеньев

Безынерционное (идеальное усилительное) звено.Это звено не только в статике, но и в динамике описывается алгебраическим уравнением

y(t) = kx(t). (3.14)

Передаточная функция:

W(s) = k. (3.15)

Амплитудно-фазовая частотная характеристика:

W(jw) = k, A(w) = k, y(w) = 0. (3.16)

Переходная и импульсная функции:

h(t) = k1(t), w(t) = kd(t). (3.17)

Безынерционное звено является некоторой идеализацией реальных звеньев. В действительности ни одно звено не в состоянии равномерно пропускать все частоты от 0 до ¥.

Примерами таких безынерционных звеньев могут служить жесткая механическая передача, часовой редуктор, электронный усилитель сигналов на низких частотах и др.

Апериодическое (инерционное) звено первого порядка.Уравнение и передаточная функция звена:

(Tp+1) y(t) = x(t), 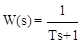, (3.18)

где T - постоянная времени, характеризует степень инерционности звена, т.е. длительность переходного процесса.

Амплитудно-фазовая частотная характеристика:

W(jw) = 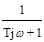, , 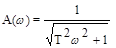y(w) = - arctgTw. (3.19)

Таким образом, апериодическое звено первого порядка является фильтром низких частот.

Переходная и импульсная функции:

h(t) = (1 - 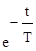), w(t) =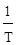 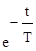. (3.20)

Примерами апериодического звена первого порядка могут служить RC цепочка, нагревательный элемент и др.

Апериодическое (инерционное) звено второго порядка.Дифференциальное уравнение звена имеет вид

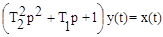, (3.21)

причем предполагается, что 2Т₂£ Т₁.

В этом случае корни характеристического уравнения вещественные и уравнение (3.21) можно переписать в виде:

( T₃p+1)(T₄p+1) y(t) = x(t), (3.22)

где 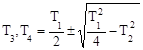- новые постоянные времени.

Передаточная функция звена

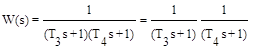. (3.23)

Из выражения (3.23) следует, что апериодическое звеновторого порядка можно рассматривать как комбинацию двух апериодических звеньев первого порядка.

Примерами апериодического звена второго порядка могут служить двойная RC цепочка, электродвигатель постоянного тока и др.

Колебательное звено.Описывается дифференциальным уравнением

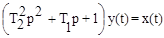, (3.24)

при Т₁<2T₂ корни характеристического уравнения комплексные и уравнение (3.24) переписывают в виде

(T²p²+2xTp+1) y(t) = x(t), (3.25)

где Т - постоянная времени, определяющая угловую частоту свободных колебаний l=1/Т;

x - параметр затухания, лежащий в пределах 0<x<1.

Общепринятая запись передаточной функции колебательного звена имеет вид

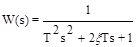. (3.26)

Амплитудно-фазовая частотная характеристика звена:

,

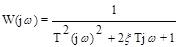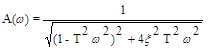, y(w) = - arctg 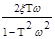. (3.27)

Временные характеристики представляют собой затухающие периодические процессы.

Примерами колебательного звена могут служить электрический колебательный контур, электродвигатель постоянного тока, маятник и др.

Консервативное звено.Консервативное звено является частным случаем колебательного при x=0. Оно представляет собой идеализированный случай, когда можно пренебречь влиянием рассеяния энергии в звене.

Амплитудно-фазовая характеристика совпадает с вещественной осью. При 0<w<1/T характеристика совпадает с положительной полуосью, а при w>1/T - с отрицательной полуосью.

Временные характеристики соответствуют незатухающим колебаниям с угловой частотой 1/T.