Представлення груп. Незвідні представлення.

Представлення груп описує абстрактні групи за допомогою лінійних перетворень векторних просторів, зокрема за допомогою матриць.

Відповідно групові операції подаються за допомогою добутку лінійних перетворень чи добутку матриць

За допомогою представлень проблеми теорії груп зводяться до простіших проблем з лінійної алгебри.

Представлення груп є одним із найважливіших знарядь у дослідженні теорії груп і мають широке застосування угеометрії, фізиці, хімії і кристалографії.

Розділ математики, що вивчає представлення груп, називається теорією представлень груп.

Представлення групи, — гомоморфізм заданої групи в групу невироджених лінійних перетворень векторного простору. Образ цього гомоморфізму є групою, елементами якої є відповідні лінійні перетворення або їх матриці. Тобто, представленням групи 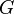, є гомоморфізм груп

,

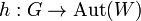де 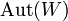позначає групу автоморфізмів векторного простору 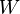. Відповідно 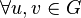маємо:

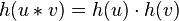
де 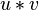— добуток елементів групи, а 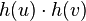— добуток лінійних перетворень, що є образами цих елементів при відображенні h.

Ізоморфність представлень[ред. • ред. код]

Нехай V і W — векторні простори над деяким тілом K. Два представлення

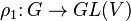і

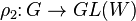
називають ізоморфними, якщо існує ізоморфізм векторних просторів:

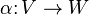
що 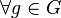виконується рівність:

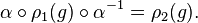
Типи представлень[ред. • ред. код]

Представлення групи в просторі, для якого існує інваріантний підпростір щодо відповідних лінійних перетворень, називається звідним; інакше - незвідним або простим.

Якщо 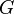— топологічна група, то під представленням 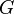звичайно розуміється неперервне лінійне представленнягрупи 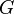у топологічному векторному просторі.

Розділи теорії представлень груп[ред. • ред. код]

Для різних видів груп представлення мають різні властивості і для їх дослідження використовуються різні математичні методи. Тому теорія представлення груп ділиться на кілька окремих розділів. Серед найважливіших зокрема є:

Теорія представлення скінченних груп. Є дуже важливою у вивченні загальних властивостей скінченних груп, також має важливі застосування у геометрії і кристалографії.

Теорія представлення компактних і локально компактних груп. Застосовує багато методів, що використовуються і для скінченних груп. Є важливою частиною гармонічного аналізу.

Теорія представлення груп Лі. Багато важливих приладів груп Лі є компактними, тож для їх дослідження використовуються методи теорії представлення компактних груп. Існують також і специфічні методи для груп Лі. Групи Лі і їх представлення широко використовуються у фізиці і хімії.

Теорія представлення лінійних алгебраїчних груп є значно менш розвинута, ніж попередні, хоча лінійні алгебраїчні групи мають багато властивостей схожих з властивостями груп Лі.

В теорії груп характером представлення групи називають функцію від елементів групи, значення якої для кожного елемента групи рівне сліду відповідної матриці.

Характер подає важливу інформацію про представлення у досить компактній формі і тому можуть бути використані для вивчення її структури. Теорія характерів є важливим інструментом у класифікації