Теорема Ліувілля про збереження фазового об’єму ансамблю механічних систем.

Теорема Ліувілля — ключова теорема гамільтонової механіки і класичної статистичної фізики. Згідно з нею, функція розподілу (густина ймовірності) гамільтонової системи залишається постійною вздовж будь-якої траєкторії уфазовому просторі, тобто, довільна область фазового простору зберігатиме свій об'єм при еволюції гамільтонової системи.

Об'єм області в фазовому просторі визначається, як

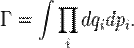
Еволюція системи задається рівняннями гамільтонової механіки. Тоді будь-яка довільно вибрана область вфазовому просторі буде змінюватися й деформуватися з часом, але згідно з теоремою Ліувілля зберігатиме свій об'єм.

Ця теорема має важливе значення для статистичної фізики.

Рівняння Ліувілля[ред. • ред. код]

Рівняння Ліувілля описує часову еволюцію функції розподілу у фазовому просторі. Хоча це рівняння носить ім'я Ліувілля, фактично його вперше опублікував Джозая Віллард Ґіббс у 1902 році[1]. Але оскільки його виведення для неканонічних систем базується на тотожності, виведеній Ліувіллем у 1838 році[2], то це рівняння носить ім'я Ліувілля.

Розглянемо гамільтонову дінамічну систему з канонічними координатами 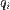та спряженими імпульсами 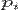, де i = 1, …, n. Тоді функція розподілу 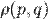визначає ймовірність 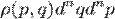того, що система знаходиться у нескінченно малому об'ємі 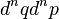фазового простору. Тоді рівняння Ліувілля визначатиме еволюцію функції розподілу 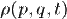у момент часу t:

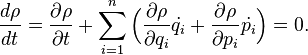
Часові похідні, що позначені крапками, визначаються з рівнянь Гамільтона. Отже, отримане рівняння демонструє збереження густини у фазовому просторі. Теорема Ліувілля стверджує, що:

Функція розподілу залишається постійною вздовж будь-якої траєкторії у фазовому просторі.

Простим доказом теореми слугує той факт, що функція розподілу 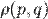задовольняє рівняння неперервності:

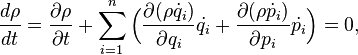
причому член,

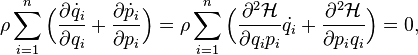
якщо використати рівняння Гамільтона, тотожно дорівнює нулю ( 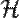— функція Гамільтона).

Наслідком теореми Ліувілля є рівняння для функції густини станів у фазовому просторі.

Незмінність об'єму довільної області в фазовому просторі означає те, що незмінною залишається ймовірність знайти систему в цьому об'ємі

,

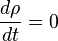де береться так звана повна похідна.

Однак сама область деформується й міняє форму. Якщо ж цікавитися фіксованим об'ємом, то з плином часу одні траєкторії входитимуть у нього, інші — виходитимуть. Баланс цих траєкторій призводить до рівняння Ліувілля

,

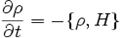де H — функція Гамільтона, а {.,.} позначає дужку Пуассона.