Принцип відносності Галілея.

Принцип відносності — це фундаментальний фізичний принцип, що включає в себе такі постулати:

Існують інерційні системи відліку (СВ) — такі СВ в яких вільний рух (при якому на тіло не діє ніяка сила) відбувається рівномірно і прямолінійно

Всі закони природи однакові в інерційних СВ.

Відрізняють два принципи відносності:

принцип відносності Галілея, в якому робиться припущення, що взаємодія між тілами відбувається миттєво. Цей принцип лежить в основі класичної механіки, з нього також випливає, що час абсолютний — він протікає однаково у будь-якій СВ;

принцип відносності Ейнштейна, в якому робиться припущення, що взаємодія між тілами поширюється з скінченною швидкістю. Цей принцип лежить в основі СТВ,створеної Енштейном. Як наслідок, в цій теорії поняття абсолютного часу немає — одна і та ж подія відбувається(триває) різний час в різних СВ.

2Зміна станів з часом. Повне рівняння Шредінгера.

Існують два принципово різні підходи до формулювання квантової механіки. І - підхід Шредінгера, ІІ - підхід Гайзенберга. У першому варіанті (Ервін Шредінгер) вектори станів змінюються з часом, а оператори - ні. У другому варіанті (Гайзенберг), навпаки, вектори станів є сталими у часі, а уся еволюція у часі перенесена на оператори.

У зображенні Шредінгера: вектори стану є функціями часу. 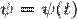Рівняння Шредінгера визначає зміну вектору стану з часом.

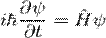
У квантовій механіці фізичним величинам не зіставляють якісь конкретні числові значення. Натомість, робиться припущення про розподіл імовірності величин вимірюваного параметра. Як правило, ці імовірності залежатимуть від виду вектору стану в момент проведення вимірювання.

Візьмемо конкретний приклад. Уявимо собі вільну частинку. Її хвильова функція - плоска хвиля. Ми хочемо визначити координату частинки. Власна функція координати частинки є дельта функцією. ( 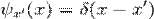) Якщо ми тепер зробимо вимірювання, то отримаємо якесь значення х'. При цьому при виконанні вимірювання ми подіяли на систему. Тепер її вектор стану вже не є плоскою хвилею. А є тією самою власною функцією оператора координати частинки.

Іноді система, що нас цікавить, не знаходиться у власному стані жодної вимірюваної нами фізичної величини. Тим не менше, якщо ми спробуємо провести вимірювання, вектор стану миттєво стане власним станом вимірюваної величини. Цей процес має назву колапсу хвильової функції. Якщо ми знаємо вектор стану в момент перед вимірюванням, то в змозі обчислити імовірність колапсу в кожний з можливих власних станів. Наприклад, вільна частинка в нашому попередньому прикладі до вимірювання буде мати хвильову функцію, яка є плоскою хвилею. Коли ми розпочинаємо вимірювання координати частинки, то неможливо передбачити результат, який ми отримаємо. Після проведення вимірювання, коли ми отримаємо якийсь результат х, хвильова функція колапсує в позицію з власним станом, зосередженим саме в х.

Деякі вектори стану призводять до розподілів імовірності, які є постійними в часі. Багато систем, які вважаються динамічними в класичній механіці, насправді описуються такими «статичними» функціями. Наприклад, електрон в незбудженому атомі в класичній фізиці зображується як частинка, яка рухається по круговій траєкторії навколо ядра атома, тоді як у квантовій механіці він є статичною, сферично-симетричною імовірнісною хмаркою навколо ядра.

Еволюція вектора стану в часі є детерміністською в тому сенсі, що, маючи визначений вектор стану в початковий момент часу, можна зробити точне передбачення того, яким він буде в будь-який інший момент. В процесі вимірювання зміна конфігурації вектора стану є імовірнісною, а не детерміністською. Імовірнісна природа квантової механіки, таким чином, проявляється саме в процесі здійснення вимірювань.