Энергия магнитного поля.

Проводник, по которому протекает электрический ток, всегда окружен магнитным полем, причем магнитное поле появляется и исчезает вместе с появлением и исчезновением тока Магнитное поле, подобно электрическому, является носителем энергии. Естественно предположить, что энергия магнитного тип работе, которая затрачивается током на создание этого поля.

Рассмотрим контур индуктивностью L, по которому течет ток I. С данным контуром скреплен магнитный поток Ф=LI, причем при изменении тока на dI магнитный поток изменяется на dФ=LdI. Однако для изменения магнитного потока на величину dФ необходимо совершить работу dA = I dФ = L I dl. Тогда работа по созданию магнитного потока Ф будет равна

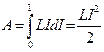
Следовательно, энергия магнитного поля, связанного с контуром,

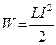(4.9.1)

Исследование свойств переменных магнитных полей, в частности распро­странения электромагнитных волн, явилось доказательством того, что энергия магнитного поля локализована в пространстве. Это соответствует представле­ниям теории поля.

Энергию магнитного поля можно предстаешь как функцию величин, характеризующих это поле в окружающем пространстве Для этого рассмотрим частный случай - однородное магнитное поле внутри соленоида. Подставив в формулу (4.9.1) выражение (4.8.2), получим

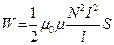
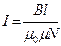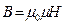Так как и , то

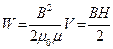(4.9.2)

Магнитное поле соленоида однородно и сосредоточено внутри него, по­этому энергия (4.9.2) заключена в объеме соленоида и распределена с постоян­ной объемной плотностью

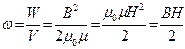(4.9.3)

Выражение (4.9.3) для объемной платности энергии магнитного поля имеет вид, аналогичный формуле для плотности энергии электростатического справедлива и для неоднородных полей. Выражение (4.9.2) справедливо для сред, в которых зависимость В от Н линейная.