Теорема Гаусса для электростатического поля.

Вычисление напряженности поля системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно значительно упростить, используя выведенную немецким ученым К.Гауссом теорему, определяющую поток вектора напряженности электрического поля через произвольную замкнутую поверхность.

В соответствии с формулой поток вектора напряженности сквозь сфе­рическую поверхность радиуса г, охватывающую точечный заряд Q, находя­щийся в ее центре (рнс.1.4.1).

,

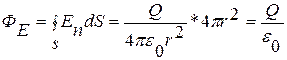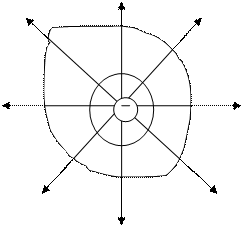Рис.1.4.1 Рис. 1.4.2

Если замкнутая поверхность произвольной формы охватывает заряд (рис.1.4.2), то при пересечении любой выбранной линии напряженности с поверхностью она то входит в нее, то выходит из нее. Нечетное число пересечений при вычислении потока, в конечном счете, сводится к одному пересечению, т.к. поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линий, входящих в поверхность.

Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, т.к. число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее.

Таким образом, для поверхности любой формы, если она замкнута и за­ключает в себя точечный заряд Q, поток вектора 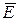будет равен 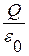т.е.

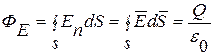(1.4.1)

Знак потока совпадает со знаком заряда Q.

Рассмотрим общий случай произвольной поверхности, окружающей n зарядов. В соответствии с принципом суперпозиции напряженность 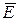поля, создается всеми зарядами, равна сумме напряженности 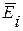, создаваемых зарядом в отдельности: 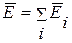. Поэтому

,

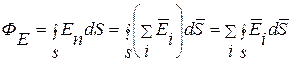Согласно (1.6), каждый из интегралов, стоящий под знаком суммы, равен 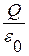. Следовательно,

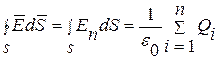. (1.4.2)

Формула(1.4.2) выражает теорему Гауссадля электростатического поля в вакууме; "поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри зарядов, деленной на 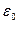.” Эта теорема выведена математически для векторного поля любой природы русским математиком М.В. Остроградсвмм, а затем независимо от него применительно к электростатическому полю - К.Гауссом.