НАГРУЖЕННОЕ РЕЗЕРВИРОВАНИЕ МАШИН В ЭКСПЛУАТАЦИИ

Надёжность машин формируется при проектировании, изготовлении и реализуется в эксплуатации. При невозможности обеспечить надежность параметрическим резервированием, применяют структурное, т.е. вводят дополнительно к основным аналогичные резервные элементы, которые включаются в работу либо одновременно с основными (нагруженное резервирование) и тогда их ресурс расходуется в процессе работы, но система продолжает функционировать после отказа без перерыва, либо резервные элементы после отказа основного устанавливаются вместо него (резервирование замещением) [1]. Нагруженное резервирование обычно используют при обеспечении надежности парка машин, когда необходимо выполнить работу в строго заданное время. Целью работы является повышение надёжности работы машин путем установления влияния технического состояния на эффективность нагруженного резервирования.

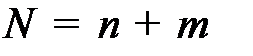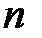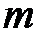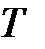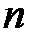В эксплуатации будет работать машин ( основних и резервних). Если средняя наработка на отказ каждой машины – , то основных машин образуют поток отказов со средней наработкой

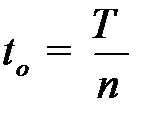. (1)

Можно полагать, что имеется одна условная машина, состоящая из n машин, отказывающая со средней наработкой 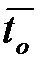и случайной наработкой между отказами 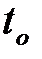. После каждого отказа одной из 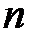машин начинается ее восстановление. Остальные машины продолжают работать [1].

Если время восстановления 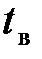меньше 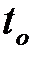, то при следующем отказе какой-либо машины, восстановленная машина (она находилась в нагруженном резерве) уже готова к работе с вероятностью определяемой ее коэффициентом готовности K_г

K_г = T / (T + 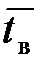), (2)

где 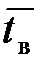– среднее время восстановления отказа одной машины.

Для часто встречающегося случая равенства коэффициентов формы (в) двух распределений случайных величин 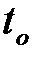и 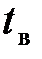, формула вероятности превышения 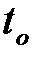над 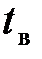имеет вид [1]

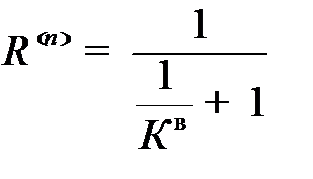, (3)

где К – коэффициент запаса, равный

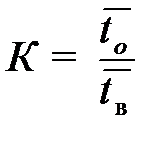. (4)

Выполнив соответствующие преобразования, получаем

R⁽ⁿ⁾ = [t_o^-в /( t_o^-в + t_o^-в) ] ∙ R⁽ⁿ⁾ = (T_o^в / T_o^в + t_o^-в) = (T/n)^в / [(T/n)^в + t_o^-в]. (5)

Вся система (из n и m машин) окажется в отказе, если откажут все резервные машины и одна условная. Вероятность такого события равна

Q^(n,m) = (1 – R⁽ⁿ⁾) ∙ (1 – R⁽¹⁾)^m (6)

Вероятность безотказной работы всей системы резерва равна [1]

R^(n,m) = 1 – (1 – R⁽ⁿ⁾) ∙ (1 – R⁽¹⁾)^m . (7)

Среднее число дополнительных машин равно

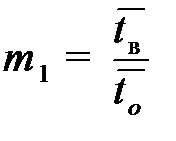, (8)

где 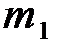округляется до ближайшего большего целого.

Теперь общее среднее число резервних машин равно

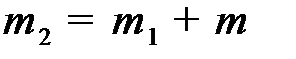. (9)

Для определения общего количества машин, необходимого для обеспечения безотказной работы парка машин с заданной вероятностью,

(например [R^(n,m)] = 0,98, b = 14, n = 10) в зависимости от коэффициента готовности К_г полученные зависимости преобразуем следующим образом.

Зная коэффициент готовности К_г и среднюю наработку на отказ каждой машины 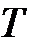, можно определить среднее время возобновления машины после отказа

t_в = [T ∙ (1 – К_г)] / К_г. (10)

После подстановки в формулу (5) зависимости (10) получаем

R⁽ⁿ⁾ = 1 / n^b ∙ [(1 / К_г – 1)^b + 1]. (11)

Далее получаем

R⁽¹⁾ = К_г^b / [1 + (1 – К_г)^b] . (12)

Уравнение 7 записываем в следующем виде

[R^(n,m)] = 1 – (1 – R⁽ⁿ⁾) ∙ (1 – R⁽¹⁾)^m. (13)

откуда

m = [lg {1 – [R^(n,m)]} – lg (1 – R⁽ⁿ⁾)] / lg (1 – R⁽¹⁾). (14)

Далее получаем

m₁ = [n^b ∙ (1 – К_г)^b] / К_г^b. (15)

Общее количество машин в парке по коэффициенту их готовности К_г = 0,9 необходимых, чтобы обеспечивать вероятность безотказной работы [R^(n,m)] = 0,98 складывается

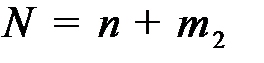, (16)

Аналогично произведен расчёт общего количества машин, необходимых для обеспечения вероятности безотказной работы [R^(n,m)] = 0,9 и 0,98 при коэффициентах их готовности К_г = 0,5; К_г = 0,7; К_г = 0,9; К_г = 1,0 для разных парков.

На основе проведенных расчетов можно сделать вывод, что для нагруженного резервирования целесообразно применять машины с коэффициентом готовности не менее 0,9…0,85. Количество необходимых резервных машин, если их коэффициент готовности меньше указанных значений, становится соизмеримым с общим количеством машин в парке.