ДИНАМИЧЕСКИЕ МОДЕЛИ, ПРИМЕНЯЕМЫЕ ДЛЯ АНАЛИЗА НАГРУЖЕННОСТИ ЗЕМЛЕРОЙНО-ТРАНСПОРТНЫХ МАШИН

Работа землеройно-транспортных машин (ЗТМ) сопровождается действием нагрузок ударного характера, воспринимаемых металлоконструкцией и гидроприводом управления рабочего оборудования. Как правило, такие нагрузки, в зависимости от конкретной ситуации, на 10-80 % превышают уровень нормального рабочего нагружения и приводят либо к ускоренному росту усталостных трещин в деталях, либо к их мгновенному разрушению. Для повышения показателей надежности ЗТМ необходимо проводить динамический анализ режимов их нагружения.

Целью статьи является исследование способов составления динамических моделей ЗТМ, позволяющих рассчитать с помощью аналитических зависимостей предельные динамические нагрузки, действующие на машины и их системы.

Общие принципы динамики строительных и дорожных машин подробно освещены в работах Т.В. Алексеевой, К.А. Артемьева, А.А. Бромберга, И.П. Бородачева, Ю.А. Ветрова, М.И. Гальперина, Н.Г. Домбровского, Ю.Л. Картвелишвили, Л.В. Назарова, А.М. Холодова и других исследователей. Характерно то, что в соответствии с современными представлениями расчет машин производится по максимальным рабочим нагрузкам при наиболее неблагоприятном взаимном расположении узлов машины. При расчете на прочность узлов машины, авторы предлагают учитывать динамическую нагрузку, возникающую во время

неустановившегося движения агрегата при взаимодействии его рабочего органа с внешней средой.

Т.В. Алексеева разработала основные подходы для оценки динамики приводов рабочего оборудования землеройных машин [1]. Основное внимание автор уделил анализу нагруженности гидравлического привода.

Д.П. Волков в работе [2] рассмотрел режимы разгона и стопорения узлов одноковшовых экскаваторов. Разработана методика определения динамической нагруженности землеройных машин. Внешняя нагрузка, воздействующая на рабочее оборудование, представляется автором в функции времени.

Закономерности неустановившегося движения машин и формирования нагрузки, действующей на рабочее оборудование, в процессе копания однородных грунтов и при взаимодействии рабочих органов с жесткими препятствиями большой массы рассмотрены в работе А. М. Холодова [3]. В данной работе автор представляет ЗТМ как одномассную или двухмассную систему, движение которой описано линейными дифференциальными уравнениями второго порядка.

Полученные А. М. Холодовым зависимости связывают максимальную нагрузку с жесткостью препятствия или интенсивностью возрастания сопротивлений при копании, массой машины и скоростью ее движения.

Особенностями данного подхода является следующее:

- не учитывается буксование движителей на этапе нарастания нагрузки на рабочем органе;

- интенсивность возрастания сопротивления на рабочем органе постоянна по пути движения машины;

- движущая сила 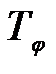является постоянной и определяется как сила тяги по сцеплению движителей;

- коэффициент упругости навесного оборудования является постоянной величиной.

Применительно к бульдозеру и автогрейдеру А. М. Холодов

рассматривает одномассную систему, представленную на рис. 1. Скрепер автор предлагает представлять в виде двухмассной динамической системы.

Действующее на рабочее оборудование горизонтальное усилие 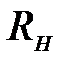определяется как сумма максимальной статической тяговой силы 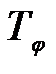и динамического усилия 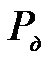за вычетом сопротивления передвижению базовой машины 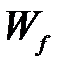[3, 4]

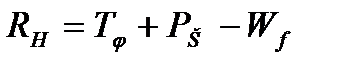. (1)

Статическое тяговое усилие, учитывая мгновенный срыв движителей в буксование

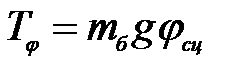, (2)

где 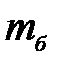– масса бульдозера;

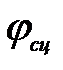– коэффициент сцепления движителей с опорной поверхностью.

Динамическое усилие 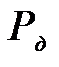А. М. Холодов предлагает определять из линейного дифференциального уравнения движения машины. Причем, в качестве расчетной величины выбирается ее максимальное значение

P_o = V_н √ А_пр∙m_б, (3)

где V_н – номинальная скорость движения машины, км\ч;

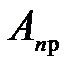– приведенная жесткость препятствия и металлоконструкции навесного оборудования, либо интенсивность возрастания сопротивлений;

m_б – масса бульдозера.

На основании анализа экспериментальных данных А. М. Холодов предлагает возрастание сопротивлений при внедрении отвала в грунт описывать линейной зависимостью, тогда интенсивность возрастания копанию можно считать постоянной [3].

Рисунок 1 – Динамическая модель бульдозера для случая интенсивного заглубления отвала в грунт, предложенная А. М. Холодовым

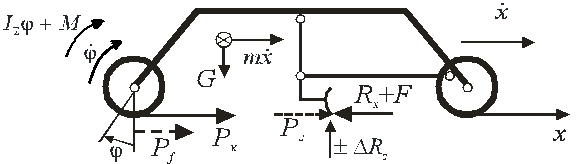
Рисунок 2 – Динамическая схема пневмоколесной землеройной машины (автогрейдера) для случая зарезания отвала, предложенная

В.М. Гольдштейном.

При упоре режущей части рабочего органа в жесткое труднопреодолимое препятствие необходимо учитывать не только жесткость рабочего оборудования, но и жесткость самого препятствия.

В. М. Гольдштейн исследовал динамическую нагруженность пневмоколесной ЗТМ в процессе выполнения ею рабочих операций на

примере автогрейдера [4]. Он обратил внимание на тот факт, что для ситуации, когда сопротивления на рабочем органе машины растут во времени не столь быстро, как в случае столкновения с жестким препятствием, динамическая схема агрегата должна представляться как двухмассная (рис. 2). При этом, по его мнению, необходимо учитывать нелинейный характер внешней характеристики двигателя внутреннего сгорания, установленного на машине и, кроме того, буксование движителей, что весьма существенно для пневмоколесных машин. Система дифференциальных уравнений, описывающая движение такой системы имеет вид

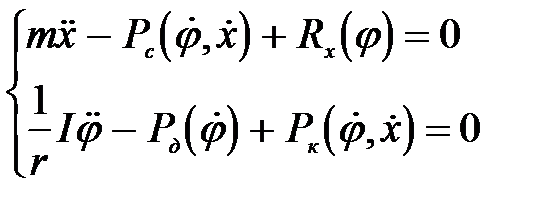. (4)

Автор отмечает, что система уравнений (4) очень сложна и получить ее решение в аналитическом виде невозможно ввиду ее существенной нелинейности. Для получения приближенного решения автор предлагает разбить весь процесс движения на участки, в пределах которых движущие силы и силы сопротивления приближенно описываются линейными уравнениями.

Ю. Л. Картвелишвили применил энергетический подход для анализа процесса столкновения рабочего органа машины с жестким непреодолимым препятствием [5, 6]. Исследования, проведенные автором, позволили выяснить, что во время резкого пикового возрастания нагрузки на рабочем органе в основном происходит деформирование конструкций и элементов системы управления исполнительного оборудования, так как они ближе всего расположены к месту зарождения удара. Ю. Л. Картвелишвили считает, что поскольку инженера интересуют только максимальные пиковые значения

действующих усилий, то динамическая схема машины может быть предельно упрощена до одно- или двухмассной системы. При этом происходит деформация только одного рабочего органа. Движущие силы со стороны

силовой установки машины, а также диссипативные силы автором не учитываются. Далее автор рассматривает для каждой массы системы уравнение энергетического баланса вида

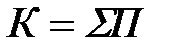, (5)

где К – кинетическая энергия движущейся массы машины (либо рабочего органа);

SП – суммарная потенциальная энергия деформации металлоконструкции рабочего оборудования или системы управления рабочим оборудованием.

Подобный подход позволил Ю.Л. Картвелишвили представить землеройную машину в виде двухмассной динамической системы (рис. 3), движение которой описывается следующими дифференциальными уравнениями

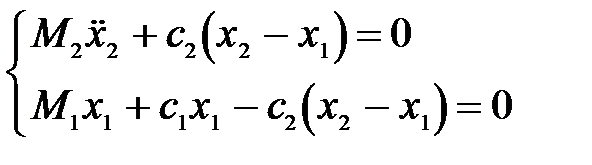, (6)

где 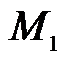, 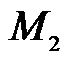– массы машины и рабочего оборудования;

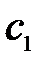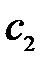, – коэффициенты упругости;

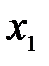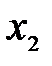, – смещения соответственно массы 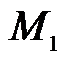и .

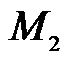Рисунок 3 – Динамическая схема землеройной машины, предложенная Ю. Л. Картвелишвили.

Рисунок 4 – Динамическая схема пневмоколесного бульдозера, предложенная Л. В. Назаровым

Поскольку коэффициенты упругости автор принимает постоянными, то решение в явном виде предложенной системы уравнений не представляет труда. При таком предельно упрощенном подходе автор, по сути дела, может определить с достаточной долей достоверности амплитуду колебания масс, а значит – максимальные значения нагрузок во время первого цикла колебания. Подобный подход не позволяет описать реальное поведение системы и изменение ее параметров в функции времени либо пути во время действия динамических нагрузок.

Исследования, проведенные Л. В. Назаровым на энергонасыщенных тракторах типа Т-150К [6], показали, что при стопорении машины в

результате упора ее рабочего органа в непреодолимое препятствие, частота оборотов коленчатого вала двигателя изменяется несущественно. При этом

избыточной мощности двигателя вполне хватает для того, чтобы практически не изменяя оборотов вала перевести пневматики в режим полного буксования. Этот факт позволил автору рассматривать пневмоколесную землеройно-транспортную машину (бульдозер) как одномассную систему (рис. 4), к которой приложена нелинейная движущая сила 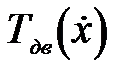. Нелинейность движущей силы объясняется наличием буксования движителей в зоне контакта с опорной поверхностью. Уравнение движения в этом случае выглядит следующим образом

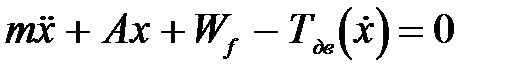, (7)

где т – поступательно движущаяся масса машины;

х – перемещение массы т.

Для того, чтобы решить уравнение (7) в явном виде, автор представлял зависимость силы тяги пневматиков от действительной скорости движения машины полиномом пятой степени, что вполне согласуется с исследованиями, проведенными представителями научной школы Н. А. Ульянова. Уравнение тягового усилия со стороны пневматиков, прикладываемого к поступательно движущейся массе, имеет вид

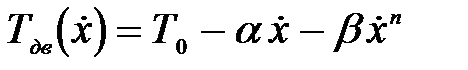, (8)

где 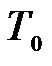– сила тяги трактора, ограничиваемая сцеплением движителей с опорной поверхностью;

a, b, n – эмпирические коэффициенты уравнения кривой .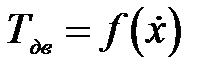

На основании выполненного анализа можно сделать следующие выводы. В соответствии с работами перечисленных авторов, общие

принципы составления динамических моделей землеройных машин следующие:

- машина представляется в виде упрощенной динамической схемы, включающей в себя сосредоточенные и распределенные массы, соединенные между собой невесомыми упругими и диссипативными элементами;

- в тех случаях, когда необходимо рассмотреть только внешнюю нагрузку, формирующуюся на рабочем органе, рассматриваются одномассные или двухмассные динамические системы. В тех ситуациях, когда необходимо точно определить усилия, возникающие в сочленениях отдельных узлов или деталей машин, рассматриваются более подробные многомассовые системы;

- движение динамической модели машины применительно к конкретному расчетному случаю описывают при помощи систем дифференциальных уравнений второй степени, сформированных на основе уравнений Лагранжа II рода или основного уравнения динамики;

- исследование уравнений движения чаще всего сводится к оценке предельных уровней действующих нагрузок, которые в дальнейшем используются для расчета по статическим критериям прочности.