Составить таблицу прогноза для исследуемых зависимостей.

Процедура 1. Расчет парного (простого) уравнения регрессии

Процедура простой регрессии заключается в нахождении аналитического выражения между двумя переменными X и Y.

Для вызова данного анализа в меню необходимо вызвать команду Relate ® Simple Regression (Связь ® Парная (простая) регрессия) (Рис.70).

Рис.70. Вызов процедуры парного регрессионного анализа

Появится окно ввода данных регрессионного анализа (Рис.71). В полях [Y:] необходимо ввести вектор данных зависимой переменной и [X:] – независимой переменной (соответственно Y – результативный признак и X – фактор).

Рис.71. Окно ввода данных процедуры парного регрессионного анализа

Заполнив поля ввода, нажмите клавишу [OK]. Система выведет на экран окно с расчетами параметров парного регрессионного уравнения связи линейной модели (рассчитывается по умолчанию линейная модель) (Рис.72):

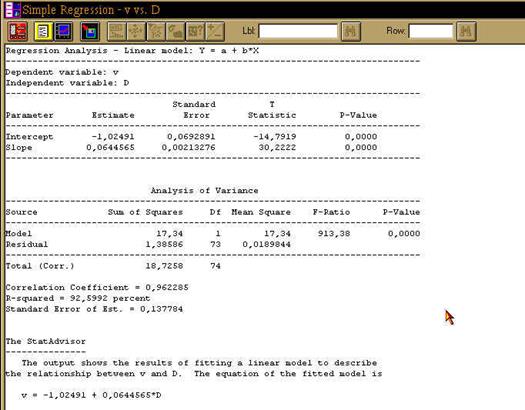
Рис. 72. Окно расчета параметров парного регрессионного уравнения связи

Процедура 2. Графическое отображение уравнения регрессии

Для графического отображения результатов нажмите кнопку графических опций [Graphical Options], появится окно выбора процедур (Рис.73). Вызовите процедуру Plot of Fitted Model (График построенной модели):

Рис. 73 Выбор графических процедур

Система построит график регрессионного уравнения по рассчитанному уравнению (Рис.74). На графике можно увидеть линию регрессии, линии доверительных интервалов и линии интервалов прогнозирования.

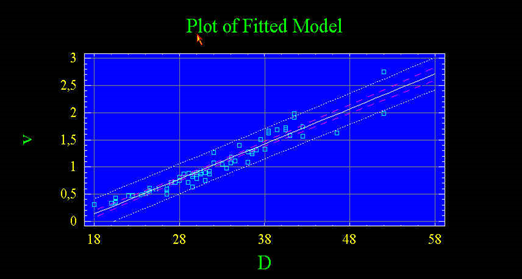
Рис.74. График построенной модели

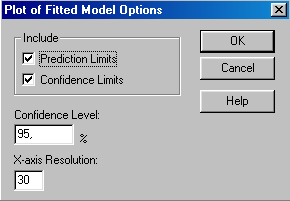
Вызовите контекстное меню в области графического отображения данных, в появившемся окне выберите команду Pane Options. Появится окно ввода опций графика рассчитанной модели (Рис.75). В верхней части окна Include задаете возможности показа на графике Confidence Limits – линий доверительных интервалов и Prediction Limits – интервалов прогнозирования. Далее задаете доверительный интервал Confidence Level:, в биологических исследованиях принимается доверительный интервал Confidence Limits = 95%. На графике (Рис.74) доверительная область обозначена пунктирной линией розового цвета.

Рис.75. Окно ввода опций графической модели

Процедура 3. Сравнение альтернативных моделей

Statgraphics Plus for Windows может производить расчет парной регрессии по 12 моделям. Название и общий вид которых представлен в табл.2.

Таблица 2

Модели парной регрессии, рассчитываемые системой Statgraphics Plus

N	Тип модели	Общий вид модели
	название русское	название английское
	Линейная	Linear	Y=a+b*X
	Экспоненциальная	Exponential	Y=exp(a+b*X)
	Обратная по Y	Reciprocal – Y	Y=1/(a+b*X)
	Обратная по Х	Reciprocal – X	Y=a+b/X
	Дважды обратная	Double Reciprocal	Y=1/(a+b/X)
	Логарифм по Х	Logarithmic – X	Y=a+ln(X)
	Мультипликативная	Multiplicative	Y=a*X^b
	Квадратный корень по Х	Square Root – X	Y=a+b*sqrt(X)
	Квадратный корень по Y	Square Root – Y	Y=(a+b*X)^2
	S-кривая	S-Curve	Y=exp(a+b/X)
	Логистическая	Logistic
		Log Probit

Нажмите кнопку табличных опций [Tabular Options] (вторая слева во втором ряду кнопок), установите флажок около процедуры Comparison of Alternative Models (Сравнение альтернативных моделей) (Рис. 76). Нажмите клавишу [OK].

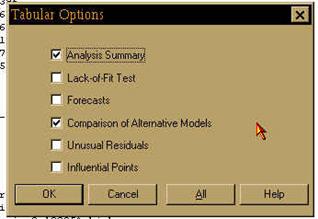
Рис. 76. Выбор процедур парного регрессионного анализа

Появится окно с одноименным именем, в котором в виде таблицы представлены результаты анализа по всем видам моделей, упорядоченные по коэффициенту корреляции R (Рис. 77).

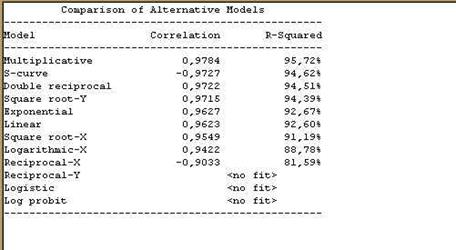
Рис.77. Результаты сравнения альтернативных моделей

По результатам аппроксимации экспериментальных данных определите наилучшую модель. В нашем случае это Мультипликативная (Multiplicative) и Дважды обратная (Double Reciprocal), т.к. коэффициенты корреляции (R) наибольшие 0,9784 и 0,9722 соответственно (Модель S-Curve не принимаем во внимание, т.к. три последние модели в табл.2 не используется в лесном хозяйстве для описания процессов).

Для проведения регрессионного анализа по наилучшим моделям вызовите контекстное меню в любой области экрана (по правой клавише мыши), выполните команду Analysis Options (Опции анализа). Появится окно выбора функций (модели перечислены в том же порядок, что и в табл.2) (Рис.78), манипулятором мышь выберите нужную модель (например, мультипликативную):

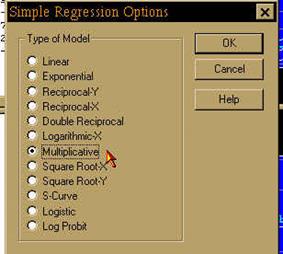
Рис.78. Выбор функции

После выбора нажмите клавишу [OK]. Появятся результаты расчета парного регрессионного анализа по мультипликативной модели (Рис. 79).

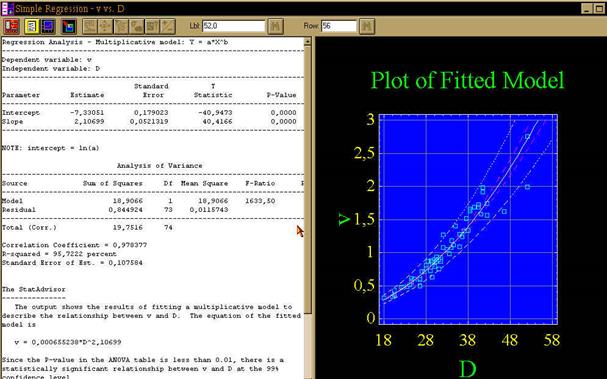
Рис.79. Результаты парного регрессионного анализа по мультипликативной модели

С экрана выпишите в табл.3 для изучаемой зависимости рассчитанные статистико-графической системой результаты для двух наилучших моделей: название модели, уравнение регрессии, коэффициент детерминации (R²) и стандартную ошибку (SE):

Таблица 3

Изучаемая зависимость	Название модели	Уравнение регрессии	R²	SE
V=f(D)	мультипликативная	V=0,000655238*D^2,10699	95,72	0,10758
дважды обратная	V=1/(-1,47318+82,4222/D)	94,513	0,16328

В процессе работы парного регрессионного анализа необходимо подобрать по две наилучшие модели для изучаемых зависимостей между лесотаксационными признаками отдельного дерева, имеющих хозяйственную значимость: диаметр дерева – объем дерева, высота дерева – объем дерева, диаметр дерева – высота дерева и выписать информацию согласно табл.3.

Сохраните результаты статистического анализа в файл, поместив его в личную папку.

Процедура 4. Составление таблиц прогноза по исследуемой зависимости

После расчета парного регрессионного анализа составьте таблицу прогноза. Для этого используйте программу MS Excel. Определите значения признака (V) по задаваемому значению фактора (D), используя наилучшую модель. Необходимо учесть при составлении таблицы прогноза, значения фактора должны находится в пределах значений экспериментальных данных (Табл.4).

Таблица 4

Объем стволов деревьев в зависимости от диаметра на высоте груди

Ступень толщины, см	Объем ствола, м³
	0,3611
	0,5303
	0,7337
	0,9722
	1,2460
	1,5557
	1,9017
	2,2843
	2,7040
	3,1609

Сохраните результаты табулирования в виде файла, поместив его в личную папку.

Лабораторная N7

Тема: Полиноминальный регрессионный анализ

Задание:

<3 4 5 678 9 >

Дата добавления: 2015-05-28; просмотров: 1168;