Лекция 8. Бета-распад

8.1. Феноменологическое рассмотрение. β-распад наблюдается у ядер с любым массовым числом, т.е. каждый химический элемент имеет β-активные изотопы. Периоды полураспада β-радиоактивных ядер лежат в интервале от 0,01 с до 10¹⁷ лет. Энергия β-распада изменяется в более широких пределах, чем при α-распаде: от 18,6 кэВ (³Н) до 16,3 МэВ (¹²N). Кроме того, в отличие от α-распада, при β-распаде образуются три новых частицы: при β^–-распаде это электрон, антинейтрино и дочернее ядро отдачи, при β⁺-распаде – позитрон, нейтрино и ядро отдачи.[65] Позитрон – античастица[66] электрона, имеющая ту же массу m_e, но положительно заряженная, – был открыт в 1932 г. К. Андерсоном в космических лучах, а в 1934 г И. Кюри и Ф. Жолио – при облучении алюминия и бора α-частицами.[67] Электроны и позитроны β-распада называют β-частицами.

Поразительной особенностью β-распада оказалась непрерывность спектра энергий испускаемых β-частиц. Их энергетический спектр простирается от 0 до некоторого максимального значения Е_β, называемого верхней границей β-спектра. Средняя энергия β-частиц составляет примерно 1/3 от Е_β. При этом, как показали калориметрические измерения, энергия, приходящаяся на долю каждой β-частицы, равна не максимальной, а именно средней энергии. Эти результаты, казалось, противоречили закону сохранения энергии. Более того, при дальнейших исследованиях обнаружилось и видимое нарушение закона сохранения момента импульса. Так как при β-распаде массовое число ядра не изменяется, спины материнского и дочернего ядер должны оставаться либо целыми (четные А) , либо полуцелыми (нечетные А), что и наблюдалось экспериментально. С другой стороны, они, очевидно, должны отличаться на ½ (спин, уносимый электроном). Наконец, опыты, в которых были измерены и сопоставлены импульсы β-частицы и ядра отдачи, указывали и на несоблюдение закона сохранения импульса.

Во избежание отказа от законов сохранения В. Паули постулировал, что при β-распаде вместе с β-частицей вылетает еще одна неизвестная и ненаблюдаемая частица с нулевым зарядом и спином ½. Эта частица уносит соответствующие доли энергии и импульса, необходимые для обеспечения законов сохранения. После открытия Чедвиком в 1932 г. нейтрона Энрико Ферми назвал ее нейтрино (т.е. «нейтрончик»). Поскольку нейтрино ускользает от наблюдения обычными ядерными методами, необходимо было предположить, что эта частица обладает очень малой или даже нулевой массой.[68] Верхний предел массы нейтрино можно определить путем очень точных измерений масс материнского и дочернего ядер и верхней границы β-спектра (для этого больше всего подходит β-распад ³Н).

Нейтрино очень слабо взаимодействует с веществом: его пробег в твердых материалах составляет ≈ 10¹⁵ км. Лишь в 1956 г. Ф. Райнэсу и К. Коуэну удалось экспериментально подтвердить существование нейтрино в опыте по поглощению его протонами с образованием нейтронов и позитронов:

p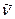⁺ + → n + e⁺.

Это пример т.н. обратного β-процесса, идущего с исключительно малой вероятностью и чрезвычайно труднодоступного для наблюдения. Путем исследования обратных β-процессов было установлено, что нейтрино, испускаемые при β⁺-распаде не идентичны тем, что получаются при β⁻-распаде (в связи с этим последние и получили название антинейтрино).

Распределить энергию β-распада между тремя частицами можно бесконечно большим числом способов. Именно поэтому энергетический спектр β-частиц и (анти)нейтрино непрерывен (при электронном захвате спектр нейтрино дискретный). Как и в случае α-распада, на ядро отдачи приходится очень малая доля энергии, а большую ее часть уносят легкие частицы. При этом, поскольку энергия распада часто сравнима с энергией покоя электрона (m_ec² = 0,511 МэВ), движение β-частиц и (анти)нейтрино описывается формулами не классической, а релятивистской механики.

Если пренебречь массой (анти)нейтрино по сравнению с массой всех других частиц, то условие энергетической разрешенности β-распада:

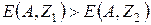
где 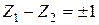, для β-распада может быть переписано в следующем виде:

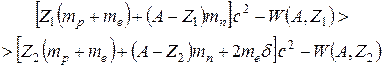
где δ = 1 для β⁺-распада и 0 для β ^–-распада и электронного захвата, или

;

.

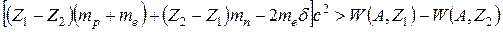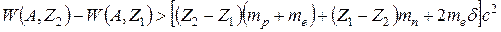Далее для каждого трех видов β-распада получим:

а) 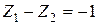, δ = 0, 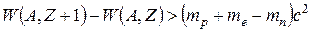= –0,789 МэВ;

б) 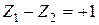, δ = 1, 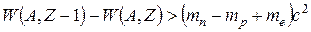= 1,811 МэВ;

в) 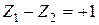, δ = 0, 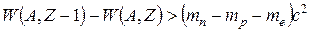= 0,789 МэВ

(здесь мы обозначили материнское ядро ).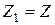

Из первого условия, в частности, видна нестабильность свободного нейтрона. Последние два условия говорят о том, что электронный захват может идти параллельно β⁺-распаду, а также когда последний запрещен энергетически.

Определим далее возможное число стабильных изобаров. Согласно формуле Вайцзеккера, сечение поверхности энергии связи плоскостью А = const − парабола. Однако в зависимости от того, является ли число нуклонов четным или нечетным, имеем два разных случая. Для изобаров с данным нечетным А имеется всего один β-стабильный нуклид (рис. 8.1), расположенный наиболее близко к минимуму параболы. В случае четных А имеем две параболы, соответствующие четно-четным (нижняя) и нечетно-нечетным (верхняя) изобарам (рис. 8.2). Как можно видеть из рисунка, для четных А могут существовать один, два или даже три стабильных изобара. Строго говоря, изобары с большей энергией при этом все-таки не вполне стабильны. Однако переход в изобар с наименьшей энергией требует процесса, при котором испускаются одновременно две β-частицы (или захватываются два электрона). Такой процесс известен под названием двойного β-распада. Его исчезающе малая вероятность приводит к тому, что периоды полураспада соответствующих нуклидов столь велики, что с трудом поддаются измерениям.[69] В заключение отметим, что, согласно рис. 8.2, нечетно-нечетные ядра могут оказаться неустойчивыми по отношению как к β^–-распаду, так и к электронному захвату, как это наблюдается у ⁴⁰К. Некоторые из них (например, ³⁶Cl) могут претерпевать и все три вида β-распада.

8.2. Замечания об электронном захвате. Процесс электронного захвата экспериментально обнаружить значительно труднее, чем β⁺- или β⁻-распад, поскольку он не сопровождается испусканием какого-либо обычного ядерного излучения (если только дочернее ядро не оказывается в возбужденном состоянии, испускающем γ-кванты). Однако вслед за электронным захватом происходит перестройка электронной оболочки атома (заполнение вакансии на внутренней орбитали). Поэтому наблюдаемым эффектом, связанным с электронным захватом, является испускание внеядерного характеристического рентгеновского излучения (см. п. 1.2), возникающего в результате заполнения вакансий в оболочке дочернего атома электронами с внешних орбиталей. Избыток энергии может вызвать также освобождение одного из атомных электронов: они называются электронами Оже.

Своеобразный характер процесса электронного захвата (не испускание, а захват электрона ядром) приводит к тому, что в данном случае постоянная распада зависит от внешних условий. Это связано с тем, что вероятность захвата прямо пропорциональна плотности электронов вблизи ядра (в смысле квадрата модуля электронной волновой функции |ψ(0)|²), которая зависит, в частности, от химической связи.[70] По этой же причине, если β⁺-распад и электронный захват одновременно разрешены энергетически, для тяжелых атомов, у которых плотность электронов вблизи ядра велика, электронный захват наиболее вероятен.

8.3. Слабое взаимодействие. Теория Ферми.На основе гипотезы Паули Ферми в 1933 г. построил количественную теорию β-распада. Основная идея Ферми заключалась в том, что β-частицы и нейтрино не существуют в ядре,[71] а рождаются в нем в процессе распада, подобно тому как фотон не является составной частью атома, а появляется непосредственно в процессе излучения. В связи с этим теория Ферми во многом похожа на теорию испускания света атомами. Однако для ее построения Ферми потребовалось ввести гипотезу о существовании особого типа короткодействующих сил, которые вызывают в ядре превращение нейтрона в протон (или протона в нейтрон) и испускание электрона и антинейтрино (или позитрона и нейтрино). Соответствующие силы отвечают т.н. слабому взаимодействию.

Для установления физического смысла слабого взаимодействия обратимся для начала к процессу рассеяния заряженных частиц. На рис. 8.3 схематично представлено столкновение двух электронов, приводящее к изменению их импульсов и энергий (диаграмма процесса). Ось времени направлена вверх. Перпендикулярно ей направлена координатная ось, условно описывающая положение частиц. Характер движения электронов (отталкивание) обусловлен электромагнитным взаимодействием. Электромагнитное поле условно обозначено волнистой линией, соединяющей точки максимального сближения частиц.

Обратимся теперь к процессу электронного захвата (рис. 8.4). Будем считать, что вначале имеются только протон (в составе ядра) и электрон. Взаимодействие между ними, не сводящееся к электромагнитному (т.е. слабое) приводит к коренным изменениям: частицы до и после взаимодействия уже не остаются теми же самыми. Тем не менее, никаких фундаментальных ограничений в виде нарушения законов сохранения для такого процесса не существует (необходимая для превращения энергия может быть получена от ядра как целого).

Дальнейшее рассуждение основано на следующем постулате. Согласно теории, получившей название квантовой теории поля, исчезновению какой-либо частицы на диаграмме процесса эквивалентно рождение ее античастицы. Заменив тогда на рис. 8.4 исчезновение электрона испусканием позитрона, мы приходим к рис. 8.5. Но такая диаграмма отвечает β⁺-распаду (направления осей в данном случае несущественны, так как они всегда могут быть выбраны нужным образом).

Аналогичной диаграммой может быть представлен и β⁻-распад (рис. 8.6). Важно то, за все три разновидности β-распада ответственно одно и то же слабое взаимодействие, или поле слабых сил. В настоящее время процессы как слабого, так и электромагнитного взаимодействия объединены в рамках электрослабой модели (ЭСМ), подтвержденной не отменяет основных результатов теории Ферми, излагаемых ниже.

8.4. Спектр β-частиц. Правило Сарджента. Рассматривая поле слабых сил действующим исключительно внутри ядра и пренебрегая кулоновским взаимодействием между дочерним ядром и β-частицей, Ферми показал, что распределение β-частиц по энергиям T_e имеет следующий вид:

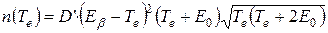, (8.1)

где D’ = const, Е₀ – энергия покоя электрона, Е_b – максимальная энергия β-спектра, практически равная энергии β-распада.[72]

В предельном случае малой энергии распада, когда каждое из допустимых значений кинетической энергии электрона 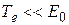, выражение (8.1) упрощается:

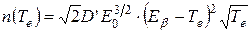. (8.2)

В другом предельном случае, когда практически все электроны можно считать ультрарелятивистскими[73], т.е. ,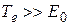

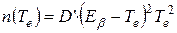. (8.3)

Графики, иллюстрирующие форму β-спектра в первом и втором случае, изображены на рис. 8.7.

Вычислим среднее значение кинетической энергии электрона в каждом из этих предельных случаев, согласно определению среднего:

.

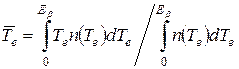В классическом пределе непосредственное интегрирование дает:

.

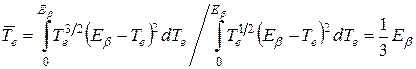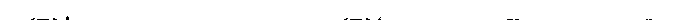Распределение (8.3), соответствующее ультрарелятивистскому пределу, симметрично относительно своей середины, поэтому

.

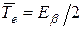Следовательно, среднее значение энергии β-частиц лежит в пределах от 1/3 до 1/2 Е_β. Поскольку ультрарелятивистские β-частицы испускаются ядрами редко, в практических расчетах часто полагают среднюю энергию β-частиц равной 1/3 отмаксимальной.

Полная вероятность вылета β-частицы находится интегрированием (8.1) по всем значениям Т_e от 0 до Е_b. Тогда постоянная β-распада

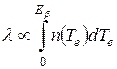. (8.4)

Результатом интегрирования является сложная, но вполне определенная функция Е_β. Если пренебречь влиянием кулоновского взаимодействия электронов и позитронов с ядром и рассматривать для простоты лишь классический и ультрарелятивистский пределы, получим

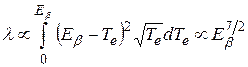, (8.5)

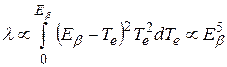, (8.6)

соответственно, так как в каждом случае результат определяется размерностью интеграла. Таким образом, постоянная β-распада зависит от энергии как (E_β)ⁿ (правило Сарджента), где n = 3,5-5, т.е. не столь исключительно сильно, как при α-распаде.

Если при β-распаде происходит образование дочернего ядра не только в основном, но и в возбужденном состоянии, суммарный β-спектр является суперпозицией нескольких парциальных β-спектров, подобных (8.1).

8.5. Ядра отдачи при β-распаде. Спектр ядер отдачи при β-распаде также непрерывен. Определим максимальную энергию ядра отдачи, выразив ее через Е_β. Импульсы β-частицы и нейтрино после распада равны р_e и р_ν соответственно. Максимальный импульс, а значит, и максимальную энергию ядро отдачи будет иметь тогда, когда векторы р_e и р_ν направлены в одну и ту же сторону. Из закона сохранения импульса в этом случае следует, что

.

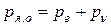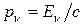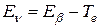Полагая любые испускаемые нейтрино ультрарелятивистскими, выразим импульс ядра отдачи через максимальную энергию β-спектра. Так как , а , то

.

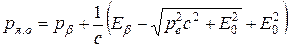Чтобы найти, при каком р_β импульс р_я.о достигает максимального значения, вычислим производную

.

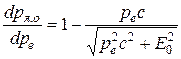Так как эта производная всегда положительна, т.е. р_я.о растет с ростом р_β, максимально возможный импульс ядра отдачи равен импульсу β-частицы, вылетающей с энергией Е_β (импульс нейтрино в этом случае равен нулю). Движение ядра отдачи можно рассматривать классическим образом, т.е.

.

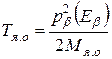Подставляя сюда квадрат импульса β-частицы с кинетической энергией, равной Е_β (см. ПРИЛОЖЕНИЕ Е), найдем, что максимальная энергия ядра отдачи

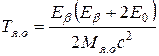. (8.7)

Так как энергия покоя ядра отдачи всегда много больше энергии покоя электрона и даже максимальной энергии β-частиц, максимальная энергия ядер отдачи при β-распаде, как правило, не превышает 10 кэВ.

8.6. Разрешенные и запрещенные β-переходы. Для огромного числа β-радиоактивных нуклидов период полураспада составляет от нескольких секунд до нескольких часов. Тем не менее, существуют и видимые исключения; среди них ⁴⁰K и ⁸⁷Rb, периоды полураспада которых измеряются миллиардами лет (п. 6.3). Теория β-распада, созданная Ферми, позволяет объяснить подобные аномалии.

Пусть имеется система частиц, начальное состояние которой описывается не зависящей от времени волновой функцией ψ_i. Пусть далее внутри этой системы возникают дополнительные силы (слабые), причем эти силы существенно меньше тех, что обеспечивают существование самой системы (сильные). За счет дополнительного слабого взаимодействия система может перейти в некоторое новое состояние ψ_f. Используя математический аппарат квантовой механики, Ферми показал, что вероятность перехода системы из состояния ψ_i в состояние ψ_f в единицу времени за счет дополнительного взаимодействия с потенциалом Ũ

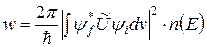, (8.8)

где n(E) – плотность конечных состояний, т.е. число состояний, приходящееся на единичный интервал энергии; интегрирование в (8.8) ведется по всему пространству. Выражение (8.8) называют золотым правилом Ферми.

Малая интенсивность слабого взаимодействия по сравнению с сильным позволяет использовать (8.8) для получения вероятности β-распада. Ниже для определенности будем говорить о β^–-распаде, когда ядро испускает электрон и антинейтрино. В этом случае в начальном состоянии существует материнское ядро, описываемое волновой функцией φ_i, а в конечном состоянии – дочернее ядро, электрон и антинейтрино, описываемые волновыми функциями φ_f, φ_e и φ_ν. Считая, что дочернее ядро, электрон и антинейтрино после разлета не взаимодействуют друг с другом, имеем для волновой функции конечного состояния ψ_f = φ_f·φ_e·φ_ν. Поскольку слабые силы – силы короткодействующие,[74] их потенциал внутри ядра может быть представлен некоторой постоянной G_F, которая получила название константы Ферми. Экспериментально установлено, что G_F = 89 эВ·фм³. За пределами ядра слабого взаимодействия нет.

Согласно введенным обозначениям, выражение (8.8) будет выглядеть как

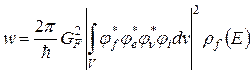. (8.9)

Стоящий в (8.9) интеграл есть мера перекрывания волновых функций начального и конечного состояний (отметим, что подынтегральное выражение отлично от нуля лишь в пределах объема ядра V). Плотность конечных состояний системы с точностью до постоянного множителя дается выражением (8.1). Если обозначить интеграл (8.4) через f₀, то можно записать

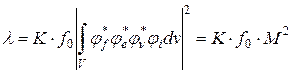, (8.10)

где К – постоянная, одинаковая для всех ядер.[75] Стоящий в (8.10) интеграл М определяется особенностями структуры ядра. Можно ожидать, что значение М не будет зависеть от энергии, и вообще будет постоянно для распада нейтрона и тех распадов, при которых не меняется конфигурация нуклонов в ядре.[76] В остальных случаях форма спектра будет определяться свойствами конкретных ядер.

Экспериментально установлено, что спектры типа (8.1) действительно наблюдаются как раз в тех случаях, когда конфигурация нуклонов не меняется при распаде. Такие спектры (например, β-спектр нейтрона) получили название разрешенных. Спектры, имеющие другую форму, называются запрещенными. Степень отклонения формы спектра от разрешенной свидетельствует о влиянии структуры ядра на β-распад. Будет ли β-распад разрешенным или запрещенным, определяется моментами и четностями материнского и дочернего ядер.

Пусть спины материнского и дочернего ядер равны J_i и J_f соответственно. Суммарный спин, уносимый электроном и антинейтрино при центральном разлете, как суммарный момент импульса пары частиц со спином ½ и относительным орбитальным моментом L = 0 может быть равен 0 или 1.[77] В этом случае закон сохранения момента импульса требует

.

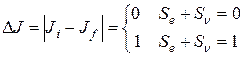Подобные процессы являются разрешенными β-переходами. При ΔJ = 0 конфигурация нуклонов в ядре не меняется и перекрывание волновых функций в (8.9) максимально. Четность при разрешенном переходе не изменяется.[78]

Если спины материнского и дочернего ядер таковы, что ΔJ > 1, относительный орбитальный момент пары электрон-антинейтрино не может быть равен нулю. В этом случае по классическим понятиям происходит нецентральный разлет частиц, вероятность которого значительно меньше. Как уже отмечалось в предыдущей лекции, нецентральный разлет приводит к необходимости преодолеть центробежный барьер, высота которого определяется формулой, аналогичной (7.17).[79] С увеличением квантового числа l, т.е. с увеличением ΔJ, увеличивается высота барьера и уменьшается вероятность туннельного эффекта. Так как вероятность тунелирования зависит от энергии частицы, энергетический спектр запрещенного β-перехода будет испытывать влияние этой зависимости и уже не будет совпадать с распределением (8.1).

Наконец заметим, что уносимая парой «электрон-антинейтрино» четность определяется ее орбитальным моментом, т.е. равна (–1)^l. Различные четности материнского и дочернего ядер требуют, чтобы l было равно 1, 3, 5… Таким образом, переходы с изменением четности обязательно будут запрещенными.[80]

Понятие запрещенного β-перехода не означает абсолютного запрета. Оно означает лишь, что вероятность запрещенного перехода существенно меньше, нежели в случае разрешенного перехода. Действительно, как показывает практика, при увеличении порядка запрета (величины ΔJ) на единицу постоянная распада радионуклида уменьшается от 10² до 10⁴ раз, в зависимости от энергии β-частиц.

Вернемся теперь к превращениям ⁴⁰K(4^–) в ⁴⁰Ca(0⁺) и ⁸⁷Rb(3/2^–) в ⁸⁷Sr(9/2⁺). Это запрещенные переходы четвертого и третьего порядка с изменением четности. Максимальные энергии β-частиц равны 1,31 МэВ для ⁴⁰K и 0,28 МэВ для ⁸⁷Rb. Поэтому неудивительно, что периоды полураспада этих нуклидов составляют 1,3 и 48 млрд. лет соответственно.