Лекция 5. Радиоактивный распад. Общие закономерности
5.1. Сущность явления радиоактивности.Открытие и изучение явления радиоактивного распада явилось первым этапом на пути познания структуры ядра и свойств элементарных частиц. Развитие исследований в этой области проходило в возрастающем темпе, начиная с конца XIX в., и продолжается в настоящее время.
В 1896 г. Анри Беккерель открыл радиоактивность урана (92U). Чуть позже было обнаружено, что радиоактивностью обладают и соединения тория (90Th). В 1898 г. Пьер Кюри и Мария Склодовская-Кюри выделили из урановой руды радий (88Ra) и полоний (84Po), радиоактивность которых оказалась в миллионы раз сильнее радиоактивности урана и тория. Однако природа радиоактивности стала понятной лишь после того, как Резерфорд и Содди показали, что радиоактивность элементов сопровождается их превращением в другие химические элементы (тем самым постулат о неизменяемости атомов был опровергнут).
Явление радиоактивности состоит в самопроизвольном распаде ядра с испусканием одной или нескольких частиц. В результате распада у ядра может измениться как заряд Z, так и массовое число А. Ядра, испытывающие самопроизвольный распад, называют радиоактивными[40], а не испытывающие – стабильными. Тем не менее, такое деление в значительной мере условно, и на практике радиоактивными считаются те ядра, распад которых может быть зарегистрирован существующими на данный момент физическими методами.
Область времен жизни радионуклидов охватывает промежутки времени от сколь угодно больших до заметно превышающих ядерное время τя = 10–22 секунды. Считается, что изменение состава ядра вследствие радиоактивного распада должно происходить не раньше, чем через 10–12 с после его рождения: за это (очень большое в ядерном масштабе) время проходят все внутриядерные процессы, и ядро успевает полностью сформироваться. Если среднее время жизни ядра меньше, чем 10–12 с, распад уже не принято считать радиоактивным. Так, при ядерных реакциях[41] образуются короткоживущие агрегаты нуклонов, которые сильно возбуждены и распадаются настолько быстро, что не могут считаться сложившимися атомными ядрами.
Радиоактивный распад характеризуется скоростью его протекания, видом испускаемых частиц и их энергией, а при вылете из ядра нескольких частиц еще и относительными углами между направлениями вылета частиц. Различают следующие основные виды радиоактивного распада: 1) α-распад; 2) β-распад; 3) γ-распад[42]; 4) спонтанное деление. Существуют и некоторые другие виды распада, наблюдающиеся достаточно редко.
При α-распаде ядро испускает α-частицу ( 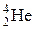 ):
):
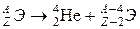 .
.
Образуется новое ядро, массовое число которого меньше, чем у исходного, на 4 единицы, а заряд – на 2 единицы, т.е. ΔА = –4, ΔZ = –2.
При β-распаде возможен один из трех следующих процессов:
а) испускание электрона и антинейтрино (β–-распад)
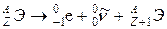 ;
;
б) испускание позитрона и нейтрино (β+-распад)
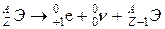 ;
;
в) захват орбитального электрона и испускание нейтрино (электронный захват)
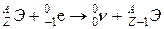 .
.
Таким образом, в процессах β-распада ΔА = 0, а ΔZ = ±1 (знак «+» соответствует β–-распаду, а знак «–» β+-распаду и электронному захвату).
Изомерный переход – это испускание ядром фотона высокой энергии (γ-кванта):
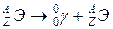
При этом заряд и массовое число ядра не изменяются, меняется лишь его энергетическое состояние.
Результатом спонтанного деления является образование двух сравнимых по массам осколков и испускание нескольких (двух-трех) нейтронов:[43]
 .
.
Необходимым (но не всегда достаточным) условием радиоактивного распада является энергетическая выгодность: масса распадающегося (материнского) ядра 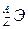 должна превышать сумму масс образующегося (дочернего) ядра
должна превышать сумму масс образующегося (дочернего) ядра 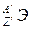 и испускаемых частиц:
и испускаемых частиц:
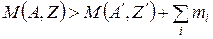 .
.
Отсюда следует, что радиоактивный распад – процесс экзотермический, т.е. идет с выделением энергии
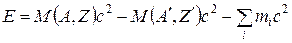 . (5.1)
. (5.1)
Выделяющаяся энергия Е – это суммарная кинетическая энергия всех продуктов распада. Как уже отмечалось, само по себе условие положительности Е еще не достаточно для того, чтобы ядро претерпевало данный вид распада. Энергетически разрешенный распад может быть запрещен другим законами сохранения: момента импульса, электрического заряда и т.п. С другой стороны, в отсутствие строгого запрета любой энергетически выгодный процесс обязательно будет происходить с той или иной (пусть исчезающее малой) вероятностью.
5.2. Основной закон радиоактивного распада. Активность.Радиоактивный распад является следствием неустойчивости ядра, или, более точно, – его состояния. Повлиять на ход распада, не изменив состояния атомного ядра, нельзя, поэтому на радиоактивный распад не оказывают влияния ни изменение температуры, давления или агрегатного состояния вещества, ни электрические и магнитные поля, ни химические реакции, в которых участвует радионуклид.[44]
Как показывают наблюдения, радиоактивный распад – процесс статистический. Так, например, в одних и тех же условиях за одинаковый промежуток времени можно зарегистрировать несколько распадов, а можно не зарегистрировать ни одного. Однако средняя скорость распада радионуклида, вычисленная по наблюдению очень большого числа распадов отдельных ядер, оказывается постоянной в любых независимых измерениях при любых условиях. В этом случае кинетика распада будет описываться следующим образом. Пусть в некоторый момент времени t имеется ансамбль из N одинаковых радиоактивных ядер. Предположим, что за время dt распадается dN ядер. Величина dN будет пропорциональна промежутку времени dt и числу ядер N:
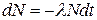 , (5.2)
, (5.2)
где λ – коэффициент пропорциональности, характеризующий среднюю скорость распада данного радионуклида и называемый постоянной распада. Знак минус означает, что с течением времени число нераспавшихся ядер уменьшается. Разделив переменные и проинтегрировав, получаем:


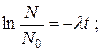
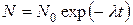 , (5.3)
, (5.3)
где N0 – число радиоактивных ядер при t = 0. Равенство (5.3) носит название основного закона радиоактивного распада.
Постоянную распада λ можно связать со средним временем жизни радиоактивного ядра τ. Для этого изобразим кривую радиоактивного распада в координатах N/N0 – t (рис. 5.1). В соответствии с математическим определением среднего значения функции (в интервале от 0 до 1),
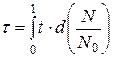 .
.
Учитывая, что значение интеграла равно площади S (заштрихована на рис. 5.1), а также то, что площадь не зависит от способа ее вычисления, имеем:
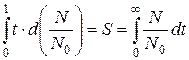 .
.
Используя (5.3), находим значение последнего интеграла:
 .
.
Таким образом, среднее время жизни ядра
 . (5.4)
. (5.4)
В качестве характеристики скорости распада радионуклида на практике чаще используют другую величину – период полураспада Т1/2. Это время, в течение которого количество ядер уменьшается в два раза. Между периодом полураспада и постоянной распада также существует простая зависимость: из (5.3) после подстановки N = N0/2 и логарифмирования получаем
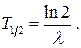 (5.5)
(5.5)
Подчеркнем еще раз, что постоянная распада λ – величина, не зависящая от времени, поскольку различные моменты времени ничем не выделены друг перед другом с точки зрения предстоящего распада ядра. В силу этого для радиоактивных ядер не существует понятия возраста: они не «стареют и не портятся». Получаемые в реакторах и ускорителях радионуклиды распадаются с той же средней скоростью, что и те же радионуклиды природного происхождения, образовавшиеся много лет назад. Именно поэтому период полураспада может использоваться для идентификации радионуклидов. Однако прежде чем перейти к методам измерения Т1/2, введем еще одно важное определение.
На практике часто приходится иметь дело с такими малыми количествами радионуклидов, когда привычные единицы измерения массы или количества вещества (грамм, моль и т.п.) оказываются более чем избыточными. С другой стороны, для определения количества радионуклида чаще всего используется регистрация испускаемого им излучения (α-, β-, γ-, нейтронов и т.п.). Поэтому целесообразнее характеризовать это количество единицами активности, т.е. числом ядер n, распадающихся за единицу времени. Активность радионуклида связана с количеством его ядер следующим образом:
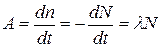 . (5.6)
. (5.6)
За единицу активности в системе СИ принимается один распад в секунду, или один беккерель (Бк). Часто используется и внесистемная единица – кюри (Ки). 1 Ки – активность такого радиоактивного образца, в котором за 1 секунду происходит 3,7·1010 распадов (1 Ки = 3,7·1010 Бк). Исторически своим появлением последняя единица обязана открытию радия: один кюри приблизительно соответствует активности одного грамма изотопа 226Ra.
Экспериментальное определение периода полураспада (постоянной распада) радионуклида осуществляют, используя детекторы излучения ядер. Зная количество ядер N и измерив с помощью детектора активность А, можно определить постоянную распада из равенства (5.6). Такой метод абсолютного счета пригоден для долгоживущих радионуклидов, активность которых в течение эксперимента (в том числе, по определению N) практически не изменяется. В противном случае используется метод прямого определения. Число частиц (α-, β-, γ-квантов, нейтронов), регистрируемых детектором за малые промежутки времени, пропорционально активности на момент измерения. В свою очередь,
 . (5.7)
. (5.7)
Таким образом, график зависимости скорости счета частиц детектором в полулогарифмических координатах – прямая, угловой коэффициент которой есть постоянная распада λ.
Метод прямого определения используют, когда период полураспада лежит в пределах от нескольких минут до нескольких дней или недель. Для более короткоживущих радионуклидов трудности, связанные с определением времени, прошедшего с начала эксперимента, в настоящее время помогают преодолеть электронные схемы, включающие и выключающие детектор через короткие и строго фиксированные промежутки времени.
5.3. Статистический характер радиоактивного распада.Как отмечалось выше, закон уменьшения числа радиоактивных ядер выполняется статистически, т.е. тем точнее, чем больше их количество. Отдельные же распады происходят совершенно случайно: предсказать, в какой момент времени распадется то или другое ядро, невозможно. Таким образом, количество распадов в единицу времени представляет собой случайную величину. В данном разделе мы найдем вид распределения этой случайной величины и установим, насколько велики могут быть отклонения скорости распада от среднего значения.
Рассмотрим распад в ансамбле из N0 радиоактивных ядер в течение времени t. Ядра ансамбля можно разбить на две группы. В первую войдут те ядра, которые распадутся за время t, во вторую – те, которые не распадутся за это время. Вероятность распада одного ядра p = 1 – q. Тогда вероятность такого сложного события, когда по истечении времени t распадутся n ядер из N0, будет равна
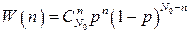 , (5.8)
, (5.8)
где 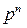 – вероятность распада n ядер первой группы,
– вероятность распада n ядер первой группы, 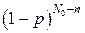 – вероятность того, что
– вероятность того, что 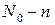 ядер второй группы при этом не распадутся,
ядер второй группы при этом не распадутся,
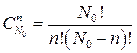 (5.9)
(5.9)
– число способов выбрать n ядер из общего числа N0. Зависимость W(n) вероятности случайного события от количественной характеристики n в полученном нами виде носит название биномиального распределения дискретной случайной величины, поскольку может быть представлена как один из членов разложения бинома Ньютона:
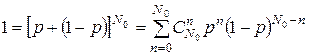
(из последнего равенства видно, что сумма вероятностей всех возможных событий равна единице). Можно показать (см. ПРИЛОЖЕНИЕ Г), что для биномиального распределения среднее значение[45]
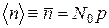 . (5.10)
. (5.10)
Реальное количество распадов, являясь случайной величиной, всегда более или менее отличается от среднего. Для оценки разброса значений случайной величины используется дисперсия D, определяемая как средний квадрат отклонения от среднего значения:
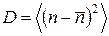 .
.
Для биномиального распределения
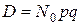 . (5.11)
. (5.11)
Закон биномиального распределения можно упростить, если выполняются следующие условия: n << N0 и р << 1, т.е. если начальное количество ядер велико, а распадаются они не слишком часто. В этом случае биномиальное распределение переходит в распределение Пуассона
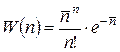 . (5.12)
. (5.12)
В отличие от биномиального распределения (5.8), характеризующегося двумя параметрами (N0 и р), оно содержит только один параметр 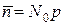 . Эксперименты по определению истинного числа распадов в единицу времени дают результаты, хорошо согласующиеся с таким распределением. Дисперсия случайной величины, распределенной по закону Пуассона,
. Эксперименты по определению истинного числа распадов в единицу времени дают результаты, хорошо согласующиеся с таким распределением. Дисперсия случайной величины, распределенной по закону Пуассона,
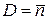 . (5.13)
. (5.13)
Данный результат следует непосредственно из (5.11), если р << 1.
Распределение Пуассона определено для целочисленных значений n. При этом через соответствующие точки можно провести плавную кривую. Для малых значений 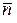 получается несимметричная кривая. По мере увеличения
получается несимметричная кривая. По мере увеличения 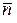 , а значит, и числа точек, кривая становится все более симметричной, причем ее максимум приходится на
, а значит, и числа точек, кривая становится все более симметричной, причем ее максимум приходится на 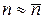 (рис. 5.2). Таким образом, при
(рис. 5.2). Таким образом, при  >> 1 число распадов можно рассматривать как непрерывную случайную величину, распределенную нормально, или по закону Гаусса:
>> 1 число распадов можно рассматривать как непрерывную случайную величину, распределенную нормально, или по закону Гаусса:
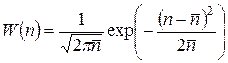 . (5.14)
. (5.14)
Дисперсия нормального распределения (5.14) связана со средним значением так же, как и в распределении Пуассона: 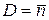 .[46]
.[46]
 Вывод среднего и дисперсии биномиального распределения, а также связь между тремя распределениями даны в ПРИЛОЖЕНИИ Г.
Вывод среднего и дисперсии биномиального распределения, а также связь между тремя распределениями даны в ПРИЛОЖЕНИИ Г.
Для определения доверительного интервала нормально распределенной величины n используют следующее выражение:
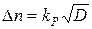 ,
,
где kP – квантиль нормального распределения, соответствующий выбранной доверительной вероятности Р. На практике при обработке экспериментальных данных часто пользуются стандартным отклонением Δn, для которого kP = 1, а Р ≈ 0,683 (т.е. среднее число распадов с вероятностью 68,3% отличается от экспериментально полученного не более чем на 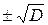 ). Величина
). Величина

представляет собой относительную ошибку измерения. Если в эксперименте зарегистрировано достаточно большое число распадов, то для определения ошибки вместо неизвестного среднего можно использовать само значение n. Так как 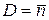 , относительная ошибка
, относительная ошибка
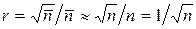 . (5.15)
. (5.15)
Отсюда следует, что для достижения заданного уровня точности измерения необходимо зарегистрировать 1/r2 распадов (например, для измерения с 1%-ной ошибкой n должно быть равно 104).
Лекция 6. Радиоактивный распад. Общие закономерности (окончание)
 6.1. Сложный распад. Последовательные и параллельные превращения.Обратимся теперь вновь к эксперименту по определению периода полураспада радионуклида. Статистический характер радиоактивного распада приводит к тому, что в реальных измерениях активности со сколь угодно совершенной аппаратурой экспериментальные точки, нанесенные на график в координатах lnA – t, всегда будут иметь разброс по обе стороны прямой, проведенной по методу наименьших квадратов. При этом следует убедиться, что стандартное отклонение не превышает
6.1. Сложный распад. Последовательные и параллельные превращения.Обратимся теперь вновь к эксперименту по определению периода полураспада радионуклида. Статистический характер радиоактивного распада приводит к тому, что в реальных измерениях активности со сколь угодно совершенной аппаратурой экспериментальные точки, нанесенные на график в координатах lnA – t, всегда будут иметь разброс по обе стороны прямой, проведенной по методу наименьших квадратов. При этом следует убедиться, что стандартное отклонение не превышает 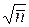 , т.е. прямая лежит внутри доверительного интервала, определенного для каждой из точек. Если провести прямую не получается (рис. 6.1), то аппаратурой регистрируется более сложное явление, чем простой распад ядер одного и того же сорта.[47] Рассмотрим различные виды сложного распада.
, т.е. прямая лежит внутри доверительного интервала, определенного для каждой из точек. Если провести прямую не получается (рис. 6.1), то аппаратурой регистрируется более сложное явление, чем простой распад ядер одного и того же сорта.[47] Рассмотрим различные виды сложного распада.
Во-первых, сложный распад может быть обусловлен тем, что исследуемое вещество содержит не один, а несколько различных радионуклидов. Тогда зависимость активности от времени будет выглядеть следующим образом:
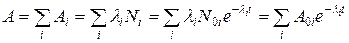 ,
,
где 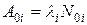 – активность i-го радионуклида в начальный момент времени. В случае смеси двух радионуклидов
– активность i-го радионуклида в начальный момент времени. В случае смеси двух радионуклидов
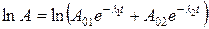 . (6.1)
. (6.1)
Если периоды полураспада радионуклидов различаются достаточно сильно (λ1 >> λ2), то при малых t показатель экспоненты при А02 близок к нулю. Тогда
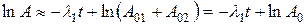 .
.
При больших t можно пренебречь первым слагаемым под логарифмом в (6.1):
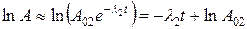 .
.
Таким образом, постоянные λ1 и λ2 определяются по угловым коэффициентам касательной к графику в точке t = 0 и асимптоты при 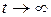 (рис. 6.1).
(рис. 6.1).
Во-вторых, в результате распада материнского ядра Э1 образующееся дочернее ядро Э2 может также оказаться радиоактивным. В этом случае мы имеем дело с последовательностью радиоактивных превращений, например
Э1 (l1) → Э2 (l2) → Э3 (l3) → …
Количество дочерних ядер каждого вида как функция времени определяется, с одной стороны, скоростью их распада и, с другой стороны, скоростью их образования, равной скорости распада соответствующих материнских ядер. Тогда, в соответствии с (5.2), получаем следующую систему дифференциальных уравнений:
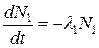 ,
,
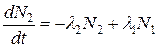 , (6.2)
, (6.2)
и т.д. Ее решение[48] для простейшего случая двух последовательных распадов при начальных условиях 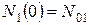 и
и 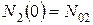 имеет вид:
имеет вид:
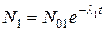 ,
,
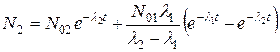 . (6.3)
. (6.3)
Отметим, что первое слагаемое в (6.3) описывает изменение во времени числа дочерних ядер, уже существовавших к начальному моменту времени. Если 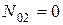 (дочернего радионуклида еще нет), то суммарная активность будет определяться следующим выражением:
(дочернего радионуклида еще нет), то суммарная активность будет определяться следующим выражением:
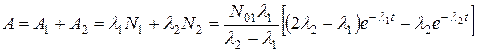 . (6.4)
. (6.4)
Рассмотрим далее два практически важных предельных случая.
A. Пусть материнский радионуклид является короткоживущим по сравнению с долгоживущим дочерним, т.е. λ1 >> λ2. Тогда из (6.4) получим
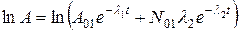 .
.
Это выражение по своему виду аналогично (6.1). Следовательно, зависимость активности от времени будет в этом случае выглядеть так же, как это изображено на рис. 6.1: материнский радионуклид очень быстро распадается, и долгоживущая активность определяется скоростью распада дочернего радионуклида.
B. Наибольший интерес представляет противоположный случай, когда дочерний радионуклид является короткоживущим по сравнению с долгоживущим материнским, т.е. когда λ2 > λ1. Из (6.3) найдем, что
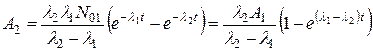 . (6.5)
. (6.5)
Логарифм суммарной активности выразится тогда как
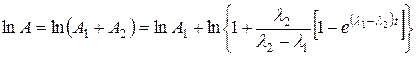 .
.
Значение экспоненты во втором слагаемом быстро стремится к нулю, поэтому на начальном отрезке времени активность быстро увеличивается, а затем медленно спадает в соответствии с изменением А1 (рис. 6.2).
Если время, прошедшее с момента t = 0, в несколько раз превышает период полураспада дочерних ядер, то
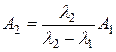 , (6.6)
, (6.6)
 т.е. активности материнского и дочернего радионуклидов в любой момент времени равны с точностью до постоянного множителя λ2/(λ2 – λ1).
т.е. активности материнского и дочернего радионуклидов в любой момент времени равны с точностью до постоянного множителя λ2/(λ2 – λ1).
|
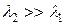 активности материнского и дочернего радионуклидов практически равны: А2 = А1. Если при этом рассматриваемый промежуток времени настолько мал по сравнению с периодом полураспада материнского радионуклида, что изменением его активности со временем можно пренебречь, говорят о вековом равновесии (в противном случае равновесие называют подвижным). В состоянии векового равновесия скорость распада дочерних ядер равна скорости их образования за счет распада материнских, т.е. dN2/dt = 0 и N2 = const.
активности материнского и дочернего радионуклидов практически равны: А2 = А1. Если при этом рассматриваемый промежуток времени настолько мал по сравнению с периодом полураспада материнского радионуклида, что изменением его активности со временем можно пренебречь, говорят о вековом равновесии (в противном случае равновесие называют подвижным). В состоянии векового равновесия скорость распада дочерних ядер равна скорости их образования за счет распада материнских, т.е. dN2/dt = 0 и N2 = const.
Наконец, рассмотрим случай, когда одни и те же ядра испытывают несколько видов радиоактивных превращений (примерами могут служить конкуренция α- и β–-распада у тяжелых ядер, β–- и β+-распада у нечетно-нечетных ядер, образование различных ядерных изомеров и т.д.).[50] Существенно то, что каждое превращение характеризуется собственной постоянной распада, определяющей его вероятность.
Пусть ядро Э1 способно превращаться в одно из ядер Эi. Уравнение для скорости распада будет тогда выглядеть как
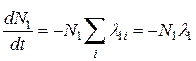 ,
,
т.е. постоянная распада λ1 есть сумма постоянных λ1i по всем возможным видам, или каналам распада. Если, в свою очередь, Эi – радиоактивное ядро, то
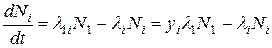 .
.
Величину
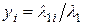 (6.8)
(6.8)
называют выходом i-го продукта превращения. Очевидно, что суммарный выход по всем каналам (как полная вероятность превращения)
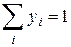 .
.
6.2. Радиоактивные цепочки.Параллельные и последовательные превращения радиоактивных ядер нередко приводят к достаточно сложным радиоактивным цепочкам, например
Э1(l1) → Э2(l2) → Э3(l3) → Э5(l5) →…→ Эn(ln) →….
 |  |  |
Э4(l4) → Э6(l6)
Как было показано Г. Бейтманом (1910 г.), для неразветвленной цепочки, состоящей из двух и более звеньев, когда при t = 0 имеется только радионуклид Э1, число ядер n-го радионуклида
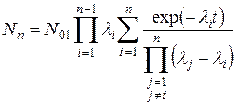 . (6.9)
. (6.9)
В том случае, когда требуется общее решение при N02, N03,… ≠ 0, его можно получить путем добавления к (6.9) аналогичных решений для более коротких цепочек, начинающихся с Э2, Э3 и т.д.
Если в цепочке последовательных превращений для любого i-го дочернего ядра λi >> λ1, то с течением времени равновесие устанавливается для всех дочерних радионуклидов, т.е. при t >> T1/2 наиболее долгоживущего продукта распада
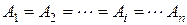 ,
,
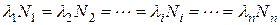 . (6.10)
. (6.10)
Закон векового равновесия, записанный в виде (6.10), можно использовать для определения периода полураспада долгоживущих материнских ядер, если предварительно определить относительное содержание каких-либо дочерних ядер в радиоактивном образце. Например, в урансодержащих минералах на каждые 2,8·106 ядер 238U приходится одно ядро 226Ra – продукта его распада с периодом полураспада 1620 лет. Используя (6.10), найдем, что период полураспада 238U составляет около 4,5·109 лет.
Если цепочка содержит разветвления, обусловленные различными каналами распада, к ней также применимо решение (6.9), однако постоянные λi, стоящие перед знаком суммы, в точках разветвления i следует умножить на величины выходов yi+1. Каждую ветвь цепочки надо просчитать независимо. Если вслед за разветвлением после ряда распадов ветви цепочки снова соединяются, число ядер за точкой соединения получается суммированием решений по всем ветвям.
6.3. Радиоактивные семейства. Радионуклиды в природе.Как отмечалось в Лекции 2, энергия связи ядра, приходящаяся на один нуклон, уменьшается с ростом массового числа A из-за возрастающей роли кулоновского отталкивания протонов. В результате тяжелые ядра становятся неустойчивыми относительно испускания α-частиц и переходят в стабильные путем одного или нескольких последовательных α-распадов. Однако в результате α-распада ядро теряет одинаковое количество протонов и нейтронов, что приводит к нарушению оптимального соотношения Z/A: образующееся дочернее ядро содержит избыточное количество нейтронов и стабилизируется путем β−-распада. Поэтому на пути превращений тяжелых радиоактивных ядер (уран, торий и др.) в стабильные наблюдается чередование процессов α- и β−-распада.
При α-распаде массовое число ядра уменьшается на четыре, а при β-распаде не изменяется. Поэтому все тяжелые радиоактивные ядра можно распределить по четырем группам, или радиоактивным семействам (табл. 6.1), в соответствии с их массовым числом 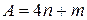 , где n − некоторое целое число, а m − остаток от деления A на четыре, т.е. 0, 1, 2 или 3. Превращение радионуклида одного семейства в радионуклид, принадлежащий другому, практически невозможно, т.к. это потребовало бы изменения массового числа на число, иное, нежели 4. Хотя такие виды радиоактивных превращений известны, выход соответствующих продуктов ничтожно мал.
, где n − некоторое целое число, а m − остаток от деления A на четыре, т.е. 0, 1, 2 или 3. Превращение радионуклида одного семейства в радионуклид, принадлежащий другому, практически невозможно, т.к. это потребовало бы изменения массового числа на число, иное, нежели 4. Хотя такие виды радиоактивных превращений известны, выход соответствующих продуктов ничтожно мал.
Таблица 6.1
Радиоактивные семейства
| А | Название | Наиболее долгоживущий родоначальник (T1/2) | Конечный стабильный нуклид |
| 4n | Ториевое | 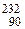 Th (1,4·1010 лет) Th (1,4·1010 лет)
| 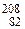 Pb Pb
|
| 4n+1 | Нептуниевое | 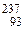 Np (2,2·106 лет) Np (2,2·106 лет)
| 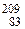 Bi Bi
|
| 4n+2 | Уран-радиевое | 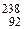 U (4,5·109 лет) U (4,5·109 лет)
|  Pb Pb
|
| 4n+3 | Уран-актиниевое | 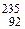 U (7·108 лет) U (7·108 лет)
|  Pb Pb
|
Радионуклиды трех семейств − ториевого, уран-радиевого и уран-актиниевого − встречаются в природе. Содержание в земной коре урана составляет 3·10−4, а тория 1·10−3 % масс. Содержание дочерних радионуклидов можно определить из соотношения (6.10), выражающего вековое равновесие, т.к. все дочерние радионуклиды имеют гораздо меньшие периоды полураспада, чем долгоживущие родоначальники. Нептуниевое семейство в природе отсутствует, и поэтому было исследовано позже остальных, лишь после того, как техника получения искусственных радионуклидов достигла достаточно высокого уровня.
Конечным продуктом распада в природных радиоактивных семействах являются изотопы свинца. Это связано с повышенной устойчивостью ядер, содержащих магическое число протонов (Z = 82). Что касается 209Bi (нептуниевое семейство), то это ядро содержит магическое число нейтронов[51] (N = 126). Именно поэтому 209Bi − самое тяжелое стабильное ядро. Заметное содержание 209Bi в земной коре может указывать на то, что много миллионов лет назад в ней присутствовали и радионуклиды семейства нептуния-237, но из-за малости периода полураспада его родоначальника перестали существовать.
Кроме представителей трех радиоактивных семейств в земной коре присутствуют еще около двадцати долгоживущих радионуклидов,[52] дающих при распаде, как правило, стабильные ядра.[53] Важнейшие из них – 40К (Т1/2 = 1,28·109 лет) и 87Rb (Т1/2 = 4,75·1010 лет).
Под действием космических лучей[54] в атмосфере Земли происходят ядерные реакции, приводящие к образованию множества радионуклидов с относительно небольшими периодами полураспада: 3Н (12,3 лет), 10Ве (1,6·106 лет), 14С и др. Эти радионуклиды получили название космогенных. Благодаря непрерывному образованию, компенсирующему их распад, космогенные радионуклиды присутствуют на Земле в количествах, достаточных для их обнаружения.
6.4. Ядерная геохронология. Ядерная геохронология использует явление радиоактивного распада для определения возраста геологических объектов. Скорость радиоактивного распада оставалась постоянной во все геологические эпохи, будучи не зависимой от внешних условий. Поэтому показания «ядерных часов», изготовленных самой природой могут считаться весьма надежными.
В настоящее время для датирования геологических объектов применяется целый ряд методов. Ядерная геохронология превратилась в самостоятельную отрасль науки о Земле. Обобщение и систематизация результатов ядерно-геохронологических исследований привели к созданию шкалы абсолютного летоисчисления Земли.[55] Совершенствование аналитической техники (главным образом, масс-спектрометрии) позволило применять при анализе одного и того же образца несколько методов. Только в том случае, если результаты, полученные разными методами, согласуются друг с другом, данному образцу приписывается определенный абсолютный возраст.
Для решения ядерно-геохронологических задач более удобна следующая запись основного закона радиоактивного распада (5.3):
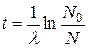 .
.
Накопившееся за время t количество ядер дочернего нуклида определяется разностью D= N0 – N, откуда следует формула для возраста образца:
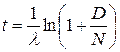 . (6.11)
. (6.11)
При выводе (6.11) предполагалось, что на момент образования объекта (минерала, породы) в его составе не было обнаружено атомов дочернего нуклида. Если же только что образовавшийся объект уже содержал D0 таких атомов, то D= D0 + N0 – N, и
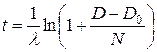 . (6.12)
. (6.12)
Следовательно, для датирования образца необходимо измерить содержание в нем материнского (радиоактивного) и дочернего (стабильного) нуклидов. Для этого чаще всего используют масс-спектрометрический анализ. Точность определения времени t, которое и принимается за абсолютный геологический возраст минерала или породы, зависит от точности определения Dи N, а также от точности, с которой известна постоянная распада λ.
Важной предпосылкой успешного использования методов ядерной геохронологии является замкнутость исследуемого образца для материнского и дочернего нуклидов. Этоозначает, что за весь период «жизни» объекта ни тот, ни другой не выносились и не добавлялись извне. Возможность частичного «открытия» в тот или иной интервал времени всегда должна учитываться. Так, при высокой температуре становится вероятной диффузия, а значит, и удаление некоторых элементов из минералов. Надежным подтверждением замкнутости системы служит совпадение возрастов, полученных разными методами, т.е. при использовании различных материнских и дочерних нуклидов.
В общей сложности разработано более десятка ядерно-геохронологических методов. Пригодность того или иного метода для оценки абсолютного возраста зависит от времени существования объекта исследования. При определении возраста молодых образований следует использовать радионуклиды со сравнительно небольшим периодом полураспада. Напротив, при исследовании древних минералов или пород требуются радионуклиды с периодом полураспада в 1 млрд. лет и больше. К наиболее широко применяемым методам относятся методы, связанные с распадом изотопов урана, 40K и 14C.
Очевидно, что максимальный возраст, установленный для земных пород, указывает нижний предел возраста Земли как планеты. Чтобы определить верхний предел возраста Земли, исследуют закономерности распределения изотопов свинца в свинцовых минералах. По современным оценкам, полученным таким методом, возраст Земли составляет 4,53 – 4,55 млрд. лет.
Уран-свинцовое датирование. Датирование по урану и свинцу является самым ранним ядерно-геохронологическим методом, использованным для определения абсолютного возраста. В 1907 г. Б. Болтвуд измерил этим методом возраст уранового минерала и сделал вывод о том, что геологические времена следует исчислять сотнями миллионов и миллиардами лет.
Средний изотопный состав свинца на Земле характеризуется следующими данными: 204Pb – 1,5%; 206Pb – 23,6%; 207Pb – 22,6%; 208Pb – 52,3%. Ядра трех последних изотопов (или часть их) являются радиогенными, представляя собой конечные продукты распада природных радиоактивных семейств.
При анализе образца на содержание изотопов U, Th и Pb можно получить три изотопных отношения: 206Pb/238U, 207Pb/235U, 208Pb/232Th. Подстановка их в (6.11) дает три независимые оценки абсолютного геологического возраста. Из-за очень большого периода полураспада Th отношение 208Pb/232Th отличается низкой чувствительностью, поэтому используется не всегда. Таким образом, сущность уран-свинцового датирования состоит, прежде всего, в определении отношений 206Pb/238U и 207Pb/235U; отсюда название метода: «уран-свинцовый». Удобными объектами для его применения являются такие урансодержащие минералы, как уранинит, циркон, монацит и др.
Если замкнутость системы нарушается, возможны потери свинца из-за диффузии. Однако если при этом все изотопы свинца теряются в одной и той же пропорции, то справедливым остается равенство
 . (6.13)
. (6.13)
Отношение 238U/235U для современной геологической эпохи постоянно и равно 137,8 практически для всех объектов. Поэтому отношение 207Pb/206Pb может служить дополнительным фактором, позволяющим по уравнению (6.13) рассчитать возраст t. Если полученное отношение согласуется с величинами, следующими из (6.11), это свидетельствует о замкнутости системы.
Присутствие первичного свинца нерадиогенного происхождения приводит, согласно (6.11), к завышению возраста урановых минералов. Можно сделать поправку на это завышение, измерив содержание нерадиогенного изотопа 204Pb. Отношения 206Pb/204Pb и 207Pb/204Pb (а также 208Pb/204Pb, если дополнительно определяется возраст по 208Pb/232Th) в радиоактивных минералах сравнивают с этими же отношениями в сопутствующих минералах, где содержание U и Th пренебрежимо мало, и все изотопы свинца можно считать нерадиогенными.
При наличии потерь урана возрасты, вычисленные по различным соотношениям, должны составлять такой ряд: t(206Pb/238U) > t(207Pb/235U) > t(207Pb/206Pb). В случае потерь свинца последовательность величин t обратная.
Калий-аргоновое датирование. Калий-аргоновый метод определения геологического возраста был разработан Э.К. Герлингом (1949 г.). Природный калий имеет радиоактивный изотоп 40К, среднее содержание которого в естественной смеси равно 0,012%. Распад 40К происходит путем β–- распада или электронного захвата. Первый канал с образованием 40Ca не имеет практического значения, так как в калийсодержащих минералах обычно присутствует нерадиогенный 40Ca, вклад которого не поддается точному учету. Второй канал ведет к образованию 40Arи используется для датирования. Долю 40К, превращающегося в 40Ar, можно подсчитать из соотношения между выходом β-распада yβ (88%) и выходом электронного захвата yе (12%):
 . (6.14)
. (6.14)
Суммарное количество радиогенных изотопов 40Ar и 40Ca, образовавшихся за время t, равно
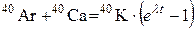 , (6.15)
, (6.15)
(λ – постоянная распада 40К). С другой стороны, из (6.14) следует, что
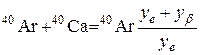 . (6.16)
. (6.16)
Сравнивая (6.15) и (6.16), получаем формулу для определения возраста:
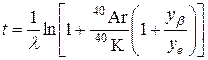 . (6.17)
. (6.17)
Калий-аргоновый метод более универсален по сравнению с уран-свинцовым, так как калийсодержащие минералы шире распространены.
Аргон, образующийся при распаде 40К, имеет тенденцию диффундировать из минералов. Для большинства минералов диффузия становится значительной при температуре > 300 оС. Скорость диффузии аргона из минерала зависит от размера его зерен: мелкозернистый минерал быстрее теряет аргон из-за большей величины отношения площади к объему. Потеря аргона вследствие диффузии приводит к тому, что для одного и того же типа минерала данной породы получаются не согласующиеся друг с другом результаты датирования. Величины такого возраста обычно занижены по сравнению с истинными, причем, чем больше потери аргона, тем в большей степени занижен кажущийся возраст. В отдельных случаях удается выявить конкретную причину несогласованности результатов определения возраста.
Радиоуглеродное датирование. В верхних слоях атмосферы изменяется состав космических лучей. Частицы первичного космического излучения (в основном, протоны) обладая высокой энергией, могут расщеплять ядра атомов, встречающихся на их пути. В результате расщеплений появляются нейтроны, которые в свою очередь могут вызывать ядерные реакции. Важнейшей реакцией, вызванной нейтронами, является превращение 14N в 14C. Космогенный 14С, называемый радиоуглеродом, имеет период полураспада 5730 лет. Испуская β-частицы, он превращается в стабильный 14N. Образуясь в атмосфере Земли, радиоуглерод быстро окисляется, превращаясь в радиоактивный углекислый газ 14СO2, который за 10-15 лет полностью перемешивается со всей массой углекислого газа атмосферы. Через углекислый газ 14С попадает в растения, а оттуда – в другие живые организмы. Равновесная концентрация 14С в обменном углероде биосферы составляет 1,2∙10-10 %.
Как только в организме прекращается обмен веществ, концентрация радиоуглерода в тканях начинает уменьшаться. Таким образом, по количеству 14С, присутствующему в остатках организмов, можно определить момент прекращения углеродного обмена с атмосферой, т.е. момент гибели. Время, прошедшее с этого момента, определяется формулой:
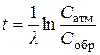 , (6.18)
, (6.18)
где Собр и Сатм – концентрации 14С в образце и атмосферном углероде; λ – постоянная распада 14С.
Радиоуглеродный метод датирования был предложен в 1951 г. В. Либби и сначала применялся для определения возраста археологических объектов органического происхождения. Радиоуглеродный метод имеет большое значение для абсолютной четвертичной хронологии. Круг объектов для датирования по 14С очень широк. Обычно используют органические остатки, встречающиеся в породах, – древесину, торф, гумус и т.д. Сравнительно небольшой период полураспада радиоуглерода ограничивает верхний предел применимости метода, который при современном уровне измерительной техники составляет 50 тыс. лет. Нижний предел применимости метода оценивается в 1 тыс. лет; объекты моложе 1000 лет нецелесообразно датировать по 14С, т.к. погрешность измерения разности между Сатм и Собр становится велика.
В основе радиоуглеродного метода лежит допущение о том, что содержание 14С во внешней среде (воздух, вода) в момент, фиксирующий прекращение обмена веществ в объекте, было таким же, как и в настоящее время. Это допущение не является вполне строгим. За последние 200 лет в результате сжигания ископаемого топлива атмосфера разбавлена техническим СО2, который практически не содержит изотопа 14С (в каменном угле и нефти концентрация радиоуглерода ничтожно мала). Термоядерные взрывы, при которых образуется большое количество нейтронов, наоборот, в отдельные периоды значительно повышали содержание 14С в атмосфере.
Кроме того, равновесная концентрация 14С в атмосфере зависит от интенсивности космического излучения. Протоны космического излучения отклоняются магнитным полем Земли, действующим подобно экрану. Судя по палеомагнитным данным, напряженность магнитного поля Земли за последние 10 тыс. лет непрерывно менялась. Соответственно этому изменялась и интенсивность потока космических протонов, достигающих верхних слоев атмосферы, а значит, и число вторичных нейтронов, ответственных за образование 14С. Это обстоятельство может вносить ошибку (порядка 10%) в результаты определения возраста радиоуглеродным методом.
Широкое применение радиоуглеродного метода датирования позволило создать климатохронологическую схему новейшего этапа геологической истории. При этом важнейшим результатом исследований было доказательство синхронных изменений климата в различных регионах Земли. Например, резко выраженное похолодание между 33 и 30 тыс. лет назад и потепление между 16,5 и 15 тыс. лет назад прослеживаются во всех частях земного шара.
Дата добавления: 2015-05-26; просмотров: 7084;
